关于CNN的复杂度分析总结
转载请注明作者和出处: http://blog.csdn.net/john_bh/
文章目录
- 1.时间复杂度
- 1.1 单个卷积层的时间复杂度
- 1.2 卷积神经网络整体的时间复杂度
- 2. 空间复杂度
- 3. 复杂度对模型的影响
- 4. Inception 系列模型是如何优化复杂度的
- 4.1 InceptionV1 中的 1x1 卷积降维同时优化时间复杂度和空间复杂度
- 4.2InceptionV1 中使用 G A P GAP GAP 代替 F l a t t e n Flatten Flatten
- 4.3 InceptionV2 中使用使用两个 3 × 3 3\times3 3×3 卷积级联替代 5 × 5 5\times5 5×5 卷积分支
- 4.4 InceptionV3 中使用 N × 1 N\times1 N×1 与 1 × N 1\times N 1×N 卷积级联替代 N × N N \times N N×N 卷积
- 4.5 Xception 中使用 Depth-wise Separable Convolution
1.时间复杂度
衡量模型的时间复杂度,常常使用模型的运算次数,FLOPs,也就是浮点运算次数(FLoating-point OPerations)。(注意)
1.1 单个卷积层的时间复杂度
T i m e : O ( M 2 ⋅ K 2 ⋅ C i n ⋅ C o u t ) Time : O(M^2 \cdot K^2\cdot C_{in}\cdot C_{out}) Time:O(M2⋅K2⋅Cin⋅Cout)
- M M M 每个卷积核输出特征图(Feature Map)的边长
- K K K每个卷积核(Kernel)的边长
- C i n C_{in} Cin每个卷积核的通道数,也即输入通道数,也即上一层的输出通道数。
- C o u t C_{out} Cout本卷积层具有的卷积核个数,也即输出通道数。
可见,每个卷积层的时间复杂度由输出特征图面积 M 2 M^2 M2、卷积核面积 K 2 K^2 K2 、输入 C i n C_{in} Cin 和输出通道数 C o u t C_{out} Cout完全决定。
其中,输出特征图尺寸本身又由输入矩阵尺寸 X X X 、卷积核尺寸 K 、 P a d d i n g 、 S t r i d e K、Padding、Stride K、Padding、Stride这四个参数所决定,表示如下:
M = ( X − K + 2 ∗ P a d d i n g ) / S t r i d e + 1 M=(X - K+2*Padding)/Stride +1 M=(X−K+2∗Padding)/Stride+1
注1:为了简化表达式中的变量个数,这里统一假设输入和卷积核的形状都是正方形。
注2:严格来讲每层应该还包含 1 个 [公式] 参数,这里为了简洁就省略了。
1.2 卷积神经网络整体的时间复杂度
T i m e : O ( ∑ l = 1 D M l 2 ⋅ K l 2 ⋅ C l − 1 ⋅ C l ) Time : O(\sum_{l=1}^{D}M_l^2 \cdot K_l^2\cdot C_{l-1}\cdot C_{l}) Time:O(l=1∑DMl2⋅Kl2⋅Cl−1⋅Cl)
- D D D 神经网络所具有的卷积层数,也即网络的深度。
- l l l 神经网络第 l l l 个卷积层;
- C l C_l Cl 神经网络第 l l l 个卷积层的输出通道数 C o u t C_{out} Cout,也即该层的卷积核个数;
- 对于第 l l l个卷积层而言,其输入通道数 C i n C_{in} Cin 就是第 l − 1 l -1 l−1 个卷积层的输出通道数。
可见,CNN整体的时间复杂度是所有卷积层的时间复杂度累加,简而言之,层内连乘,层间累加。
2. 空间复杂度
空间复杂度(访存量),严格来讲包括两部分:总参数量 + 各层输出特征图。
- 参数量:模型所有带参数的层的权重参数总量(即模型体积,下式第一个求和表达式)
- 特征图:模型在实时运行过程中每层所计算出的输出特征图大小(下式第二个求和表达式)
S p a c e : O ( ∑ l = 1 D K l 2 ⋅ C l − 1 ⋅ C l + ∑ l = 1 D M l 2 ⋅ C l ) Space: O(\sum_{l=1}^{D} K_l^2\cdot C_{l-1}\cdot C_{l} + \sum_{l=1}^{D}M_l^2\cdot C_{l}) Space:O(l=1∑DKl2⋅Cl−1⋅Cl+l=1∑DMl2⋅Cl)
总参数量只与卷积核的尺寸 K K K 、通道数 C C C 、层数 D D D 相关,而与输入数据的大小无关。
输出特征图的空间占用比较容易,就是其空间尺寸 M 2 M^2 M2和通道数 C C C 的连乘。
注:实际上有些层(例如 ReLU)其实是可以通过原位运算完成的,此时就不用统计输出特征图这一项了。
3. 复杂度对模型的影响
- 时间复杂度决定了模型的训练/预测时间。如果复杂度过高,则会导致模型训练和预测耗费大量时间,既无法快速的验证想法和改善模型,也无法做到快速的预测。
- 空间复杂度决定了模型的参数数量。由于维度诅咒的限制,模型的参数越多,训练模型所需的数据量就越大,而现实生活中的数据集通常不会太大,这会导致模型的训练更容易过拟合。
- 当我们需要裁剪模型时,由于卷积核的空间尺寸通常已经很小(3x3),而网络的深度又与模型的表征能力紧密相关,不宜过多削减,因此模型裁剪通常最先下手的地方就是通道数。
4. Inception 系列模型是如何优化复杂度的
通过五个小例子说明模型的演进过程中是如何优化复杂度的。
4.1 InceptionV1 中的 1x1 卷积降维同时优化时间复杂度和空间复杂度
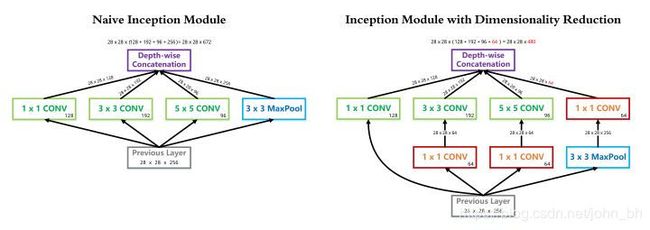
InceptionV1 借鉴了 Network in Network 的思想,在一个 Inception Module 中构造了四个并行的不同尺寸的卷积/池化模块(上图左),有效的提升了网络的宽度。但是这么做也造成了网络的时间和空间复杂度的激增。对策就是添加 1 x 1 卷积(上图右红色模块)将输入通道数先降到一个较低的值,再进行真正的卷积。
以 InceptionV1 论文中的 (3b) 模块为例(可以点击上图看超级精美的大图),输入尺寸为 28 × 28 × 256 28\times28\times256 28×28×256, 1 × 1 1\times1 1×1 卷积核 128 128 128 个, 3 × 3 3\times3 3×3 卷积核 192 192 192 个, 5 × 5 5\times5 5×5 卷积核 96 96 96 个,卷积核一律采用 Same Padding 确保输出不改变尺寸。
在 3 × 3 3\times3 3×3 卷积分支上加入 64 64 64个 1 × 1 1\times1 1×1 卷积前后的时间复杂度对比如下式:
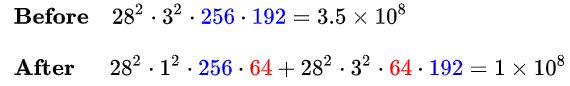
同理,在 5 × 5 5\times5 5×5卷积分支上加入 64 64 64 个 1 × 1 1\times1 1×1卷积前后的时间复杂度对比如下式:
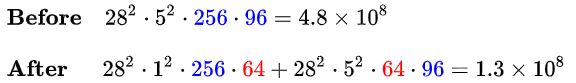
可见,使用 1 × 1 1\times1 1×1 卷积降维可以降低时间复杂度3倍以上。该层完整的运算量可以在论文中查到,为 300 M,即 3 × 1 0 8 3\times10^8 3×108 。
另一方面,我们同样可以简单分析一下这一层参数量在使用 1 × 1 1\times1 1×1卷积前后的变化。可以看到,由于 1 × 1 1\times1 1×1卷积的添加, 3 × 3 3\times3 3×3 和 5 × 5 5\times5 5×5 卷积核的参数量得以降低 4 倍,因此本层的参数量从 1000 K 降低到 300 K 左右。
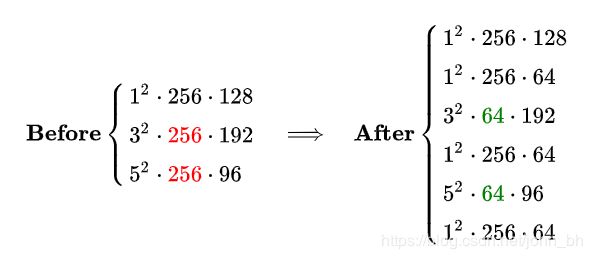
4.2InceptionV1 中使用 G A P GAP GAP 代替 F l a t t e n Flatten Flatten
全连接层可以视为一种特殊的卷积层,其卷积核尺寸 K K K 与输入矩阵尺寸 X X X 一模一样。每个卷积核的输出特征图是一个标量点,即 M = 1 M=1 M=1 。复杂度分析如下:
T i m e : O ( 1 2 ⋅ X 2 ⋅ C i n ⋅ C o u t ) Time : O(1^2\cdot X^2 \cdot C_{in}\cdot C_{out}) Time:O(12⋅X2⋅Cin⋅Cout)
S p a c e : O ( X 2 ⋅ C i n ⋅ C o u t ) Space: O( X^2 \cdot C_{in}\cdot C_{out}) Space:O(X2⋅Cin⋅Cout)
可见,与真正的卷积层不同,全连接层的空间复杂度与输入数据的尺寸密切相关。因此如果输入图像尺寸越大,模型的体积也就会越大,这显然是不可接受的。例如早期的VGG系列模型,其 90% 的参数都耗费在全连接层上。
InceptionV1 中使用的全局平均池化 GAP 改善了这个问题。由于每个卷积核输出的特征图在经过全局平均池化后都会直接精炼成一个标量点,因此全连接层的复杂度不再与输入图像尺寸有关,运算量和参数数量都得以大规模削减。复杂度分析如下:
T i m e : O ( C i n ⋅ C o u t ) Time : O( C_{in}\cdot C_{out}) Time:O(Cin⋅Cout)
S p a c e : O ( C i n ⋅ C o u t ) Space: O( C_{in}\cdot C_{out}) Space:O(Cin⋅Cout)
4.3 InceptionV2 中使用使用两个 3 × 3 3\times3 3×3 卷积级联替代 5 × 5 5\times5 5×5 卷积分支
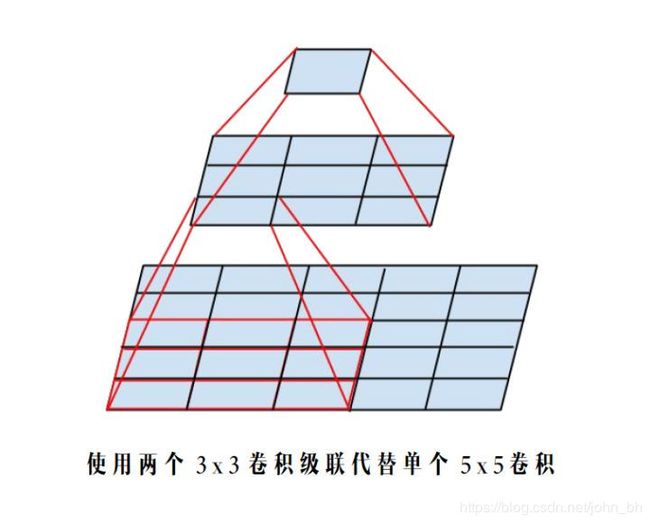
根据上面提到的二维卷积输入输出尺寸关系公式,可知:对于同一个输入尺寸,单个 5 × 5 5\times5 5×5 卷积的输出与两个 3 × 3 3\times3 3×3 卷积级联输出的尺寸完全一样,即感受野相同。同样根据上面提到的复杂度分析公式,这种替换能够非常有效的降低时间和空间复杂度。我们可以把辛辛苦苦省出来的这些复杂度用来提升模型的深度和宽度,使得我们的模型能够在复杂度不变的前提下,具有更大的容量,爽爽的。
同样以 InceptionV1 里的 (3b) 模块为例,替换前后的 5 × 5 5\times5 5×5 卷积分支复杂度如下:
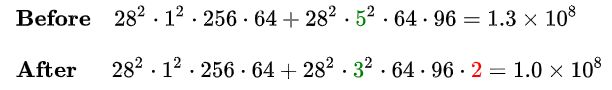
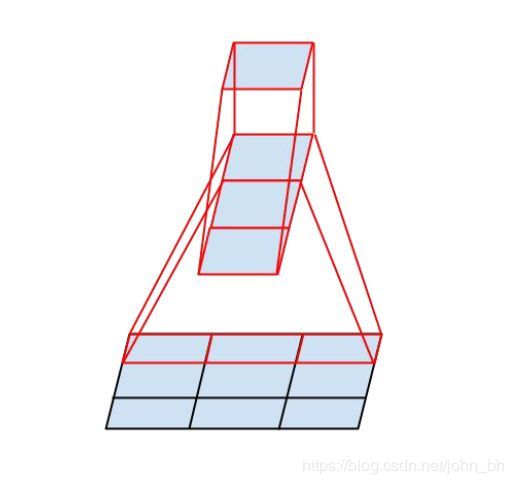
4.4 InceptionV3 中使用 N × 1 N\times1 N×1 与 1 × N 1\times N 1×N 卷积级联替代 N × N N \times N N×N 卷积
InceptionV3 中提出了卷积的 Factorization,在确保感受野不变的前提下进一步简化.
4.5 Xception 中使用 Depth-wise Separable Convolution
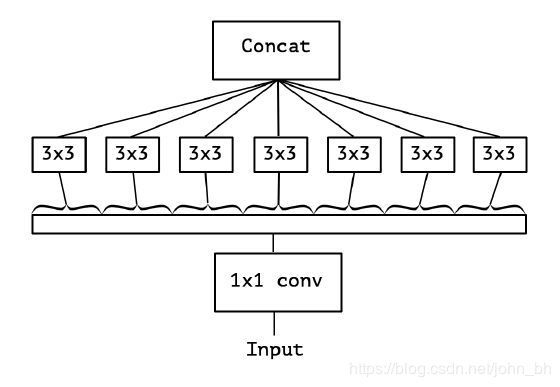
之前讨论的都是标准卷积运算,每个卷积核都对输入的所有通道进行卷积。Xception 模型挑战了这个思维定势,它让每个卷积核只负责输入的某一个通道,这就是所谓的 Depth-wise Separable Convolution。
从输入通道的视角看,标准卷积中每个输入通道都会被所有卷积核蹂躏一遍,而 Xception 中每个输入通道只会被对应的一个卷积核扫描,降低了模型的冗余度。
标准卷积与可分离卷积的时间复杂度对比:可以看到本质上是把连乘转化成为相加。
S t a n d a r d C o n v o l u t i o n T i m e : O ( M 2 ⋅ K 2 ⋅ C i n ⋅ C o u t ) Standard\ Convolution\ Time: O( M^2\cdot K^2\cdot C_{in}\cdot C_{out}) Standard Convolution Time:O(M2⋅K2⋅Cin⋅Cout)
D e p t h − w i s e S e p a r a b l e C o n v o l u t i o n T i m e : O ( M 2 ⋅ K 2 ⋅ C i n + M 2 ⋅ C i n ⋅ C o u t ) Depth-wise\ Separable\ Convolution\ Time: O( M^2\cdot K^2\cdot C_{in}+ M^2\cdot C_{in}\cdot C_{out}) Depth−wise Separable Convolution Time:O(M2⋅K2⋅Cin+M2⋅Cin⋅Cout)
参考链接:
Xception: Deep Learning with Depthwise Separable Convolutions
卷积神经网络的复杂度分析