坐标变换(2)—不同坐标系下的变换

如下图所示，在自动驾驶车辆上会存在大量冗余的传感器，例如轮速传感器、激光雷达，毫米波雷达，摄像头，超声波雷达，GPS，IMU等。不同传感器对同一物体的测量原始结果都是在自身坐标下，所以首先我们需要对多传感器就行标定(即获得不同坐标系之间的变换关系，多传感器的标定是个非常复杂且困难的问题，这里先不介绍)，将所有传感器的输出统一到一个坐标系下。

本文主要介绍不同坐标系之间变换的原理，在这里我们采用一个体系，即存在一个世界坐标系，我们定义的位置或者姿态都是参考世界坐标系或者世界坐标系定义的笛卡尔坐标系，且讨论的维度为3维。

1. 位置、姿态与坐标系

1.1 位置

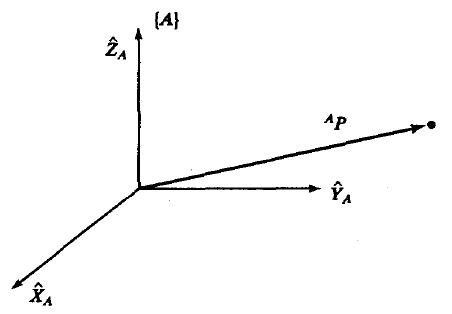
一旦我们定义了一个坐标系，对于空间中某一点的位置我们就能用一个$3\times 1$的列向量来表示。如图1所示，我们在世界坐标系下还定义了很多坐标系，所以在定义位置向量时，必须附加一个条件，表明是哪个坐标系下的。

在本文中，我们用左上标来描述具体的坐标系，例如${}^{A}P$表明列向量$P$在坐标系$A$下定义的。

$${}^{A}P=\left[\begin{array}{l}{p}_x\\ p_y\\ p_z\end{array}\right]$$

1.2 姿态

为了描述物体的姿态，我们将在物体上固定一个坐标系，并且给出此坐标系相对于参考坐标系的表达。所以位置用列向量描述，姿态可以用固定在物体上的坐标系描述。

这里我们定义参考坐标系$A$，用$X_A,Y_A,Z_A$表示坐标系$A$ 的三个主轴的单位向量，而${}^A{X}_B{,}^A{Y}_B{,}^A{Z}_B$ 为坐标系$B$的三个主轴的单位向量(相对于参考坐标系$A$)，并利用${}^A{X}_B{,}^A{Y}_B{,}^A{Z}_B$顺序排列，组成了一个$3\times 3$ 的矩阵，称为旋转矩阵，用符号${}_B^{A}R$表示，

$${}_B^{A}R=\left[\begin{array}{ccc}{}^A{X}_B& {}^A{Y}_B& {}^A{Z}_B\end{array}\right]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$

其中，标量$r_{ij}$也可以利用坐标系$B$对应主轴在参考坐标系$A$中各主轴的投影来表示(利用内积求每个坐标轴的投影值)，

$${}_B^{A}R=\left[\begin{array}{ccc}{}^A{X}_B& {}^A{Y}_B& {}^A{Z}_B\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{X}}_{\mathbf{B}}\cdot {\mathbf{X}}_{\mathbf{A}}& {\mathbf{Y}}_{\mathbf{B}}\cdot {\mathbf{X}}_{\mathbf{A}}& {\mathbf{Z}}_{\mathbf{B}}\cdot {\mathbf{X}}_{\mathbf{A}}\\ {\mathbf{X}}_{\mathbf{B}}\cdot {\mathbf{Y}}_A& {\mathbf{Y}}_{\mathbf{B}}\cdot {\mathbf{Y}}_A& {\mathbf{Z}}_{\mathbf{B}}\cdot {\mathbf{Y}}_{\mathbf{A}}\\ {\mathbf{X}}_{\mathbf{B}}\cdot {\mathbf{Z}}_{\mathbf{A}}& Y_{\mathbf{B}}\cdot Z_A& {\mathbf{Z}}_{\mathbf{B}}\cdot {\mathbf{Z}}_{\mathbf{A}}\end{array}\right]$$

在上式最右边矩阵中省略了上标，事实上只要点积的各对向量是在同一坐标系中描述的，那么坐标系的选择可以是任意的。由于上式右边矩阵中的向量均为单位向量，所以通过内积计算的结果是两者之间夹角的余弦，所以上述矩阵也称为方向余弦矩阵。

由上式可以看出，矩阵的行是单位向量$\{A\}$在$\{B\}$中的描述( 即${}^B{X}_A$ )，即，

$${}_B^{A}R=\left[\begin{array}{ccc}{}^A{X}_B& {}^A{Y}_B& {}^A{Z}_B\end{array}\right]=\left[\begin{array}{c}{}^B{X}_A^T\\ {}^B{Y}_A^T\\ {}^B{Z}_A^T\end{array}\right]$$

进而，可以得到，

$${}_B^{A}R={{}_A^{B}R}^T$$

而，

$$\left[\begin{array}{c}{}^A{X}_B^T\\ {}^A{Y}_B^T\\ {}^A{Z}_B^T\end{array}\right]\left[\begin{array}{ccc}{}^A{X}_B& {}^A{Y}_B& {}^A{Z}_B\end{array}\right]={{}_B^{A}R}^T{}_B^{A}R=I_3$$

从而还得到旋转矩阵是一个正交矩阵。

1.3 坐标系

在自动驾驶中，位置和姿态总是成对出现的，我们将此组合称为坐标系。一个坐标系可以等价的用一个位置向量和一个旋转矩阵来描述。

例如，我们用${}_B^{A}R$和${}^A{P}_{BORG}$来描述坐标系$B$，而参考坐标系为$A$。其中${}^A{P}_{BORG}$是坐标系$B$在参考坐标系$A$中的原点的位置向量，而${}_B^{A}R$是坐标系$B$的姿态。

2. 坐标变换

这里的坐标变换指的是将一个坐标系中的向量在其他坐标系中进行变换(描述)，向量本身并没有变换，只不过对它的描述变换了。

2.1 平移变换

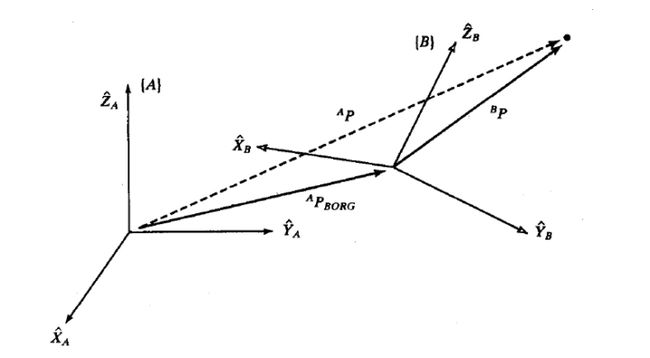
如下图3所示，

在坐标系$B$中，我们用向量${}^{B}P$描述了其中一个位置，现在要将该向量变换到坐标系$A$中，也就是将该向量在$A$中进行描述，这里假设 $A$和$B$的姿态相同，易得，

$${}^{A}P={}^{B}P+{}^A{P}_{BORG}$$

2.2 旋转变换

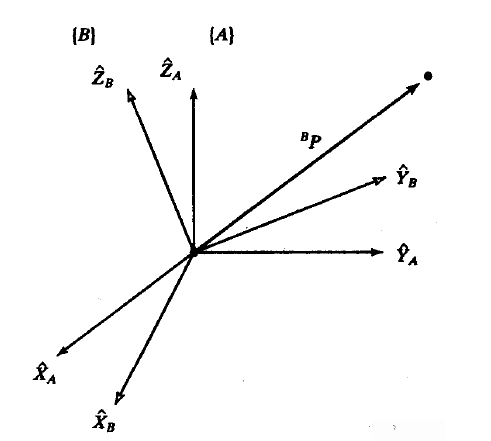
如下图所示，

我们用${}_B^{A}R$表示坐标系$B$在参考坐标系$A$中的描述，现在已知参考系$B$中的位置向量${}^{B}P$，求其在参考坐标系$A$中的描述？

我们知道，一个位置向量在其参考坐标系中的三个轴的分量都是该向量在对应三个轴上的投影，而投影的大小可以利用向量的点积进行计算。因此我们可以将${}^{A}P$的分量计算如下，

$$\begin{array}{r}{}^A{p}_x={}^B{X}_A\cdot {}^{B}P\\ {}^A{p}_y={}^B{Y}_A\cdot {}^{B}P\\ {}^A{p}_z={}^B{Z}_A\cdot {}^{B}P\end{array}$$

上面式中，我们首先将坐标系$A$在坐标系$B$中去描述， 前面介绍过，只要点积的各对向量是在同一坐标系中描述的，那么坐标系的选择可以是任意的。这里${}^B{X}_A$和${}^{B}P$都是在坐标系$B$下描述，所以可以利用点积直接计算出${}^{B}P$在$x$轴方向的投影。将上面三式写成矩阵形式，由前面可知，${}_B^{A}R$的行就是${}^B{X}_A$,${}^B{Y}_A$,${}^B{Z}_A$。

$${}^{A}P={}_B^{A}R{}^{B}P$$

有个便于记忆的小技巧，前面的矩阵的下标$B$消去了后面矩阵的上标 $B$ 。

2.3 旋转平移

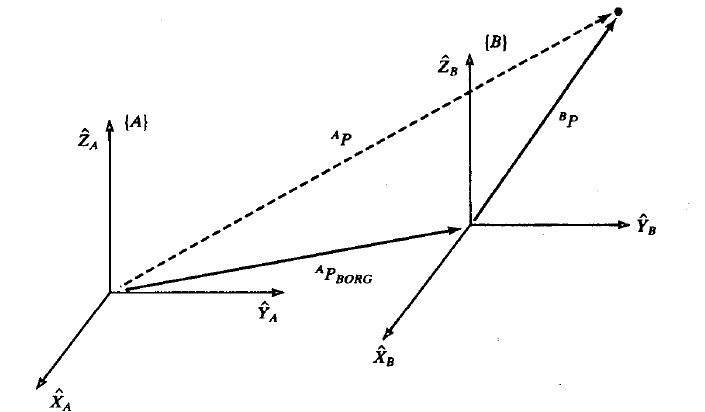
考虑下面的情况，既有平移，又有旋转，如何求 ${}^{A}P$ ？

首先，我们将${}^{B}P$ 变换到一个中间的过渡坐标系，这个坐标系和 $A$ 的姿态相同，原点和 $B$ 重合。然后再利用简单的向量加法将向量进行平移，即

$${}^{A}P={}_B^{A}R{}^{B}P+{}^A{P}_{BORG}$$

但是上述公式不是线性的，利用一点数学变换，可以得到一个更简单的公式，

$$\left[\begin{array}{c}{}^{A}P\\ 1\end{array}\right]=\left[\begin{array}{cc}{}_B^{A}R& P_{BORG}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{}^{B}P\\ 1\end{array}\right]$$

所以可以变换成下式统一的格式，

$${}^{A}P={}_B^{A}T{}^{B}P$$

其中，称 $T$ 为 $4\times 4$ 其次变换矩阵。