分治法-----快速排序、归并排序、堆排序

十种常见排序算法可以分为两大类：

**非线性时间比较类排序：**通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此称为非线性时间比较类排序。

**线性时间非比较类排序：**不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此称为线性时间非比较类排序。

0.2 算法复杂度

0.3 相关概念

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。

不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。

空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

下面主要看三种排序方法：

1、快速排序
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数（不要被这个名词吓到了，就是一个用来参照的数，待会你就知道它用来做啥的了）。为了方便，就让第一个数6作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在6的右边，比基准数小的数放在6的左边，类似下面这种排列：

3 1 2 5 4 6 9 7 10 8
在初始状态下，数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置，假设这个位置是k。现在就需要寻找这个k，并且以第k位为分界点，左边的数都小于等于6，右边的数都大于等于6，递归对左右两个区间进行同样排序即可。想一想，你有办法可以做到这点吗？这就是快速排序所解决的问题。

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。它的平均时间复杂度为O(nlogn)，最坏时间复杂度为O(n^2).

首先上图：

从图中我们可以看到：

left指针，right指针，base参照数。

其实思想是蛮简单的，就是通过第一遍的遍历（让left和right指针重合）来找到数组的切割点。

第一步：首先我们从数组的left位置取出该数（20）作为基准（base）参照物。(如果是选取随机的，则找到随机的哨兵之后，将它与第一个元素交换，开始普通的快排)

第二步：从数组的right位置向前找，一直找到比（base）小的数，如果找到，将此数赋给left位置（也就是将10赋给20），此时数组为：10，40，50，10，60， left和right指针分别为前后的10。

第三步：从数组的left位置向后找，一直找到比（base）大的数，如果找到，将此数赋给right的位置（也就是40赋给10），此时数组为：10，40，50，40，60， left和right指针分别为前后的40。

第四步：重复“第二,第三“步骤，直到left和right指针重合，最后将（base）放到40的位置， 此时数组值为： 10，20，50，40，60，至此完成一次排序。

第五步：此时20已经潜入到数组的内部，20的左侧一组数都比20小，20的右侧作为一组数都比20大， 以20为切入点对左右两边数按照"第一，第二，第三，第四"步骤进行，最终快排大功告成。

快速排序代码如下：

//快速排序，随机选取哨兵放前面
void QuickSort(int* h, int left, int right)
{

	if(h==NULL) return;
	if(left>=right) return;
 //防止有序队列导致快速排序效率降低 
	 srand((unsigned)time(NULL));
	 int len=right-left;
	 int kindex=rand()%(len+1)+left;
	 Swap(h[left],h[kindex]);
     int key=h[left],i=left,j=right;
	 while(i=key && i

}

(编辑器的格式调整的不顺利，将就看)

2、归并排序

基本思想
　　归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

分而治之

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

合并相邻有序子序列
　　再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

算法实现：

//归并排序
void MergeArray(int* arr, size_t left, size_t mid, size_t right, int* temp)
{

if(arr==NULL) return;

size_t i=left,j=mid+1,k=0;
while(i<=mid && j<=right)
{
    if(arr[i]<=arr[j])
    {
        temp[k++]=arr[i++];
        continue;
    }
    
    temp[k++]=arr[j++];
}

while(i<=mid)
    temp[k++]=arr[i++];
    
while(j<=right)
    temp[k++]=arr[j++];
    
memcpy(&arr[left],temp,k*sizeof(int));
    
return;

}

void MMergeSort(int* arr, size_t left, size_t right, int* temp)
{

if(left

}

void MergeSort(int* h, size_t len)
{

if(h==NULL) return;
if(len<=1) return;
int* temp=(int*)calloc(len,sizeof(int));
MMergeSort(h, 0, len-1, temp);

memcpy(h,temp,sizeof(int)*len);

free(temp);

return;

}

3、堆排序

堆排序实际上是利用堆的性质来进行排序的，要知道堆排序的原理我们首先一定要知道什么是堆。
堆的定义：
堆实际上是一棵完全二叉树。
堆满足两个性质:
1、堆的每一个父节点都大于（或小于）其子节点；
2、堆的每个左子树和右子树也是一个堆。
堆的分类：
堆分为两类：
1、最大堆（大顶堆）：堆的每个父节点都大于其孩子节点；
2、最小堆（小顶堆）：堆的每个父节点都小于其孩子节点；

堆的存储：
一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如下图所示：

堆排序：
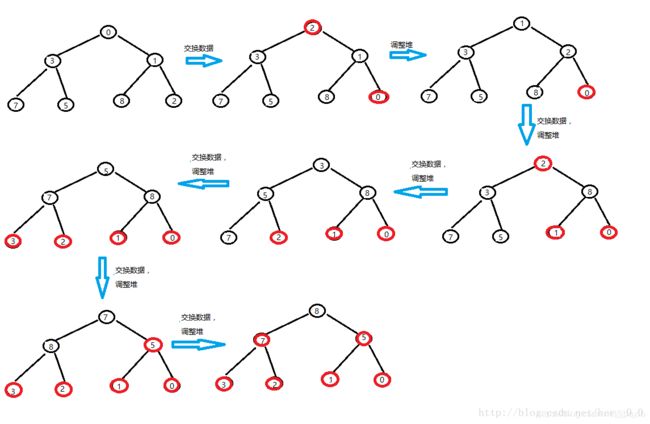
由上面的介绍我们可以看出堆的第一个元素要么是最大值（大顶堆），要么是最小值（小顶堆），这样在排序的时候（假设共n个节点），直接将第一个元素和最后一个元素进行交换，然后从第一个元素开始进行向下调整至第n-1个元素。所以，如果需要升序，就建一个大堆，需要降序，就建一个小堆。
堆排序的步骤分为三步:
1、建堆（升序建大堆，降序建小堆）；
2、交换数据；
3、向下调整。
假设我们现在要对数组arr[]={8,5,0,3,7,1,2}进行排序（降序）：
首先要先建小堆：

堆建好了下来就要开始排序了：

现在这个数组就已经是有序的了。

算法实现：
//堆排序
/*
大顶堆sort之后，数组为从小到大排序
/
//调整=
void AdjustHeap(int h, int node, int len) //----node为需要调整的结点编号，从0开始编号;len为堆长度
{

int index=node;
int child=2*index+1; //左孩子，第一个节点编号为0 
while(child=h[child]) break;
    Swap(h[index],h[child]);
    index=child;
    child=2*index+1;
}

}

//建堆=
void MakeHeap(int* h, int len)
{

for(int i=len/2;i>=0;--i)
{
    AdjustHeap(h, i, len);
}

}

//排序=
void HeapSort(int* h, int len)
{

MakeHeap(h, len);
for(int i=len-1;i>=0;--i)
{
    Swap(h[i],h[0]);
    AdjustHeap(h, 0, i);
}

}

转自https://www.cnblogs.com/fnlingnzb-learner/p/9374732.html