python学习——day07

本文参与「少数派读书笔记征文活动」https://sspai.com/post/45653

参考文章：http://www.cnblogs.com/graceting/p/3877214.html

首先，归结今天遇到的问题：

1.主函数：Python使用缩进对齐组织代码的执行，所有没有缩进的代码（非函数定义和类定义），都会在载入时自动执行，这些代     码，可以认为是Python的main函数。为了区分主执行文件还是被调用的文件，Python引入了一个变量__name__，当文件是被调     用时，__name__的值为模块名，当文件被执行时，__name__为'__main__'  

   典型的Python文件结构：

2.缩进：python采用标准的4个空格缩进，Pycharm设置缩进：File->Setting->Editor->Code Style->Python
3.raw_input()：将所有输入作为字符串看待，返回字符串类型；直接读取控制台的输入（任何类型的输入它都可以接收）

#raw_input() 将所有输入作为字符串看待
a = raw_input("input:")
>>> input:123
type(a)
>>>               # 字符串
a = raw_input("input:")
>>> input:runoob
type(a)
>>>               # 字符串

#input() 需要输入 python 表达式
a = input("input:")
>>> input:123                  # 输入整数
type(a)
>>>                # 整型
a = input("input:")    
>>> input:"runoob"           # 正确，字符串表达式
type(a)
>>>              # 字符串
a = input("input:")
>>> input:runoob               # 报错，不是表达式
Traceback (most recent call last):
  File "", line 1, in 
  File "", line 1, in 
NameError: name 'runoob' is not defined

4.跟踪异常：

import traceback
try:
    1/0
except Exception e:
    #print e    #只报错，不能了解哪个文件哪个函数哪一行出错
    traceback.print_exc()    #直接打印，还可接受file参数直接写入到一个文件
    #traceback.format_exc()   #返回字符串

5.pycharm科学模式(Scientific Mode)：
如果主要利用python进行数据分析，可以采用科学模式，具体介绍见：http://www.jetbrains.com/help/pycharm/matplotlib-support.html
6.控制台闪退：将python程序打包成可执行文件后运行，程序出错时会闪退，可以在程序中使用try...except捕获异常，并在except末尾加上os.system("pause")
备注：
1.只添加os.system("pause")不捕获异常，仍然会闪退
2.如果是GUI程序且程序正常运行不需要控制台，可以加上-w参数：pyinstaller -w -F xxx.py
7.python文件的关闭函数close()：
txt=open("xxx.txt","r").read() 返回的是字符串txt，不是文件句柄，所有txt.close()无效；此语句后程序会自动关闭文件。

 

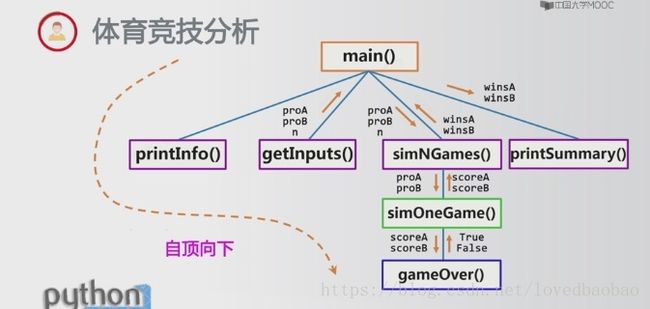
实例1（体育竞技分析：模拟N场比赛——室内排球）

-输入：球员的水平
-输出：可预测的比赛成绩

比赛规则：
-双人击球比赛：A&B,回合制，5局3胜(1-4局25分，第五局15分，且每局比分相差2分及以上)
-开始时一方先发球，直至判分，接下来胜者发球

-计算思维：抽象+自动化
-模拟：抽象比赛过程+自动化执行N场比赛

自顶向下
-将一个总问题表达为若干个小问题组成的形式
-使用同样方法进一步分解小问题
-直至，小问题可以用计算机简单明了的解决

自底向上（执行）
-分单元测试，逐步组装
-按照自顶向下相反的路径操作
-直至，系统各部分以组装的额思路都经过测试和验证

第一阶段：程序总体框架及步骤（步骤->函数->参数）
步骤：
1.打印程序的介绍性信息        -printIntro()
2.从用户处获得程序运行参数：运动员A/B的能力值以及模拟比赛的场次、数量    -getInputs()
3.利用球员的能力值，模拟n场比赛（即n次模拟一场比赛）    -simNGames()
4.输出球员A和B获胜比赛的场次及概率        -printSummary()

# CalSportCompeV1.py

#排球运动

import random
import os

#打印提示信息
def printInfo():
	print("这个程序模拟两个选手A和B的某种竞技比赛：")
	print("程序运行需要A和B的能力值（以0到1之间的小数表示）：")


#获取输入信息
def getInputs():
	proA = eval(input("请输入选手A的能力值（0-1）："))
	proB = eval(input("请输入选手B的能力值（0-1）："))
	n = eval(input("模拟比赛的场次："))
	return proA, proB, n


def simNGames(proA, proB, n):
	countA, countB = 0, 0
	for i in range(n):          #n场模拟依次进行
		if SimOneGame(proA, proB) == 1:     #A方赢
			countA += 1
		else:       #B方赢
			countB += 1
	return countA, countB


def SimOneGame(proA, proB):
	#随机决定发球方（正式排球比赛中，通常以抛硬币的方式决定）
	temp=0.5
	while temp == 0.5:
		temp = random.random()
	if temp<0.5:
		serve = "A"  # 发球方
	else:
		serve="B"

	setA,setB=0,0       #赢的回合数
	while not gameOver(setA,setB):
		scoreA, scoreB = 0, 0       #每回合的分数
		while not setOver(scoreA, scoreB,setA+setB+1):      #每回合的最后一分肯定是此回合胜方所发，所以不需要再手动设定发球方
			if serve == "A":
				if random.random() < proA:      #A方赢
					scoreA += 1
				else:
					scoreB+=1
					serve = "B"
			else:
				if random.random() < proB:      #B方赢
					scoreB += 1
				else:
					scoreA+=1
					serve = "A"

		if scoreA>scoreB:
			setA+=1
		else:
			setB+=1

	return (1 if (setA > setB) else 0)

#判断回合是否结束
def setOver(scoreA, scoreB,sets):
	if sets==5:         #若比赛进行到第5回合
		if scoreA >= 15 or scoreB >= 15:
			if(abs(scoreA-scoreB)>=2):      #满15分相差2分及以上才算结束
				return True
			else:       #未满15分
				False
		else:
			return False
	else:           #第1-4回合
		if scoreA >= 25 or scoreB >= 25:
			if(abs(scoreA-scoreB)>=2):       #满25分相差2分及以上才算结束
				return True
			else:
				return False
		else:       #未满25分
			return False

#判断比赛是否结束
def gameOver(setA,setB):
	if setA==3 or setB==3:      #先赢三局者获胜
		return True
	else:
		return False

#输出最终结果
def printSummary(countA, countB):
	print("选手A获胜{0}场比赛，占比{1:.2f}%".format(countA, countA / (countA + countB) * 100))
	print("选手B获胜{0}场比赛，占比{1:.2f}%".format(countB, countB / (countA + countB) * 100))


#主函数
#main()
if __name__ == "__main__":
	printInfo()
	proA, proB, n = getInputs()
	print("竞技分析开始，共模拟{}场比赛".format(n))
	countA, countB = simNGames(proA, proB, n)
	printSummary(countA, countB)
	#os.system("pause")

输出：
这个程序模拟两个选手A和B的某种竞技比赛：
程序运行需要A和B的能力值（以0到1之间的小数表示）：
请输入选手A的能力值（0-1）：0.66
请输入选手B的能力值（0-1）：0.7
模拟比赛的场次：1000
竞技分析开始，共模拟1000场比赛
选手A获胜277场比赛，占比27.70%
选手B获胜723场比赛，占比72.30%
(ps:即使是看起来很小的差距，场次多了，差距还是大呀)

计算思维：第3种人类思维特征

python学习方法

应用开发的四个步骤：
1.产品定义：对应用需求充分理解和明确定义
2.系统架构：以系统方式思考产品的技术实现
3.设计与实现：结合架构完成关键设计与系统实现
4.用户体验：从用户角度思考应用效果

安装Python第三方库：

Python社区：PyPI(Python Package Index) https://pypi.org/

方法1：使用pip命令
pip install <库名>：安装
pip install -U <库名>：更新
pip uninstall <库名>：卸载
pip download <库名>：下载但不安装
pip show <库名>:列出库的详细信息
pip search <关键词>：根据关键词和库名搜索库
pip list:当前系统已经安装的库

方法2：集成安装方法
Anaconde开发环境：支持近800个第三方库(https://www.anaconda.com/)
包含多个主流工具
适合数据计算领域开发

方法3：文件安装方法
*有些第三方库没有提供可执行文件而是源文件，安装前需要编译
UCI页面：https://www.lfd.uci.edu/~gohlke/pythonlibs/
给出了windows系统上第三方库编译后的可执行文件

OS库：提供通用的、基本的操作系统交互功能（Windows、Mac OS、Linux）

路径操作：os.path子库，处理文件路径及信息

函数	描述
os.path.abspath(path)	返回path在当前系统中的绝对路径
os.path.normpath(path)	归一化path的表示形式，同一用\\分隔符
os.path.relpath(path)	返回当前程序与文件之间的相对路径
os.path.dirname(path)	返回path中的目录名称 os.path.dirname("D://PYE//file.txt") >>>  'D://PYE'
os.path.basename(path)	返回path中最后的文件名称 os.path.basename("D://PYE//file.txt") >>> 'file.txt'
os.path.join(path,*paths)	组合path与paths，返回一个路径字符串 os.path.join("D:/","PYE/file.txt") >>> 'D:/PYE/file.txt'
os.path.exists(path)	判断path所对应文件或目录是否存在，返回True或False
os.path.isfile(path)	判断path所对应是否为已存在的文件，返回True或False
os.path.isdir(path)	判断path所对应是否为已存在的目录，返回True或False
os.path.getatime(path)	返回path对应文件或目录上一次的访问时间（可用time库格式化） time.ctime(os.path.getatime("D:/PYE/file.txt")) >>> 'Sun Feb 11 21:43:53 2018'
os.path.getmtime(path)	返回path对应文件或目录最近一次的修改时间
os.path.getctime(path)	返回path对应文件或目录的创建时间
os.path.getsize(path)	返回path对应文件的大小，以字节为单位

获取当前目录路径和上级路径

import os

#获取当前目录
print(os.getcwd())
print(os.path.abspath(os.path.dirname(__file__)))
#获取上级目录
print(os.path.abspath(os.path.dirname(os.path.dirname(__file__))))
print(os.path.abspath(os.path.dirname(os.getcwd())))
print(os.path.abspath(os.path.join(os.getcwd(),"..")))
#获取上上经济目录
print(os.path.abspath(os.path.join(os.getcwd(),"../..")))

进程管理：启动系统中其他程序
os.system(command)
-执行程序或命令command
-在Windows系统中，返回值为cmd的调用返回信息

import os
os.system("C:\\Windows\\System32\\calc.exe")         #运行计算机程序
>>> 0

os.system("C:\\Windows\\System32\\mspaint.exe \
F:\\PycharmProjects\\project1\\data\\pywcloud2.png")      #运行画图工具，并自动打开一张图片

环境参数：获得系统软硬件信息等环境参数

函数	描述
os.chdir(path)	修改当前程序操作的路径
os.getcwd	返回程序的当前路径
os.getlogin()	获得当前系统登录用户名称
os.cpu_count()	获得当前系统的CPU数量
os.urandom(n)	获得n个字节长度的随即字符串，通常用于加解密运算

实例2：第三方库自动安装脚本

（友情提示：别在pycharm中运行，在控制台用python运行就好，否则容易卡掉。。。）

库名	用途
NumPy	N维数据表示和运算
Matplotlib	二维数据可视化
PIL	图像处理
Scikit-Learn	机器学习和数据挖掘
Requests	HTTP协议访问及网络爬虫
Beautiful Soup	HTML和XML解析器
Wheel	Python第三方库文件打包工具
Django	Python最流行的Web开发框架
Flask	轻量级Web开发框架
WeRoBot	微信机器人开发框架
SymPy	数学符号计算工具
Pandas	高效数据分析和计算
Networks	复杂网络和图结构的建模和分析
PyQt5	基于Qt的专业级GUI开发框架
PyOpenGL	多平台OpenGL开发接口
PyPDF2	PDF文件内容提取及处理
docopt	Python命令行解析
PyGame	简单小游戏开发框架

#BatchInstall.py

import os
import traceback

libs={"matplotlib","pillow","sklearn","requests","beautifulsoup4","wheel",\
      "networks","sympy","django","flask","werobot","pyqt5","pandas",\
      "pyopengl","pypdf2","docopt","pygame"}
global lib

try:
	for lib in libs:
		os.system("pip3 install "+lib)
		print("Successful——"+lib)
except:
	print("Failed Somehow——"+lib)
	traceback.print_exc()

一、从数据处理到人工智能

数据表示(用程序表达)->数据清洗(归一化、数据转换、异常值处理)->数据统计(数量、分布、中位数等)->数据可视化->数据挖掘(获取、产生数据外的价值)->人工智能(数据/语言/图像/视觉等方面深度分析与决策)

Python库之数据分析

• Numpy:表达N维数组的最基础库 http://www.numpy.org/
• Pandas:Python数据分析高层次应用库  http://pandas.pydata.org/ 
  Series=索引+一维数据
  DataFrame=行列索引+二维数据
• SciPy:数学、科学和工程计算功能库 https://www.scipy.org/
  傅里叶变换、信号处理类、线性代数类、图像处理类、稀疏图压缩类、稀疏图运算类、优化算法类

Python库之数据可视化

• Matplotlib:高质量的二维数据可视化功能库 https://matplotlib.org/
• Seaborn:统计类数据可视化功能库 http://seaborn.pydata.org/
• Mayavi:三位科学数据可视化功能库 http://docs.enthought.com/mayavi/mayavi/

Python库之文本处理

• PyPDF2:用来处理pdf文件的工具箱 http://mstamy2.github.io/PyPDF2/
• NLTK:自然语言文本处理（支持语言文本分类、标记、语法句法、语义分析等） http://www.nltk.org/
• Python-docx:创新或更新Microsoft Word文件的第三方库 http://python-docx.readthedocs.io/en/latest/index.html

Python库之机器学习

• Scikit-learn:机器学习方法工具集 http://scikit-learn.org/
  -提供一批统一化的机器学习方法功能接口
  -提供聚类、分类、回归、强化学习等计算功能
• TensorFlow:AlphaGo背后的机器学习计算框架  http://www.tensorflow.org/
• MXNet:基于神经网络的深度学习计算框架 http://mxnet.incubator.apache.org/
  -提供可扩展的神经网络及深度学习计算功能
  -可用于自动驾驶、机器翻译、语音识别等众多领域 

import numpy as np
from PyPDF2 import PdfFileReader,PdfFileMerger
from nltk.corpus import treebank #corpus是保留字
from docx import Document
import tensorflow as tf

#Numpy
def npSum():
	a=np.array([0,1,2,3,4])
	b=np.array([9,8,7,6,5])
	c=a**2+b**3

	return c

print(npSum())

#PyPDF2
merger=PdfFileMerger()      #pdf文件合并
input1=opne("document1.pdf","rb")
input2=open("document2.pdf","rb")
merger.append(fileobj=input1,pages(0,3))
merger.merge(position=2,fileobj=input2,pages(0,1))
output=open("document-output.pdf","wb")
merger.write(output)

#NLTK
t=treebank.parsed_sents('wsj_0001.mrg')[0]
t.draw()

#Python-docx
document=Document()
document.add_heading('Document Title',0)    #标题
p=document.add_paragraph('A plain paragraph having some') #段落
document.add_page_break()   #分页符
document.save('demo.docx')      #生成外部文件

#TensorFlow
init=tf.global_variables_initializer()
sess=tf.Session()
sess.run(init)
res=sess.run(result)
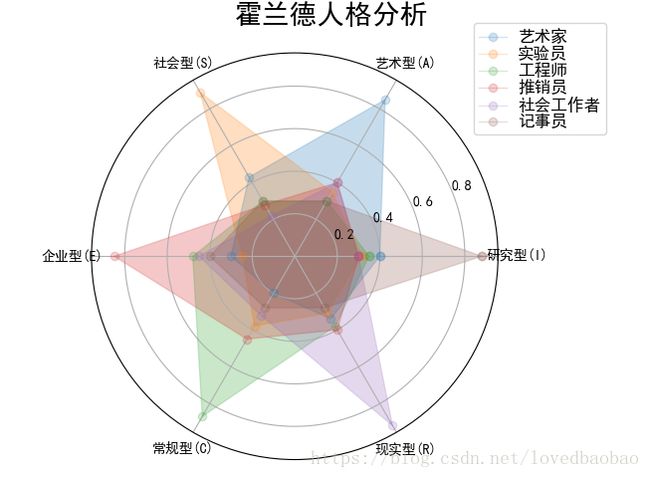
print('result:'+res)

实例3：霍兰德人格分析雷达图

-需求：雷达图方式验证霍兰德人格分析
-输入：各职业人群结合兴趣的调研数据

#HollandRadarDraw

import numpy as np
import matplotlib.pyplot as plt
import matplotlib

"""
The font.family property has five values: 'serif' (e.g., Times), ## 'sans-serif' (e.g., Helvetica), '
cursive' (e.g., Zapf-Chancery), ## 'fantasy' (e.g., Western), and 'monospace' (e.g., Courier).  
Each of ## these font families has a default list of font
"""
matplotlib.rcParams['font.family']='SimHei'   #黑体
radar_labels=np.array(['研究型(I)','艺术型(A)','社会型(S)','企业型(E)','常规型(C)','现实型(R)'])
#            艺术家 实验员 工程师 推销员 社会工作者 记事员
data=np.array([[0.40,0.32,0.35,0.30,0.30,0.88],   #研究型
               [0.85,0.35,0.30,0.40,0.40,0.30],   #艺术型
               [0.43,0.89,0.30,0.28,0.22,0.30],   #社会型
               [0.30,0.25,0.48,0.85,0.45,0.40],   #企业型
               [0.20,0.38,0.87,0.45,0.32,0.28],   #常规型
               [0.34,0.31,0.38,0.40,0.92,0.28]])  #现实型
#数值的大小用"圆半径"表示
data_labels=("艺术家","实验员","工程师","推销员","社会工作者","记事员")

"""
numpy.linespace(start,stop,num=50,endpoint=True,retstep=False,dtype=None)
在制定的间隔内返回均匀间隔的数字
num:整数，可选，默认=50，即样本的数量，不可为负
endpoint:端点，可选，默认=True，即包含stop点
dtype:输出数组的类型，可选，如果不给出具体值，则自动参考输入变量
step:浮点数，可选，当restep=True时，返回样本的间距
"""
angles=np.linspace(0,2*np.pi,6,endpoint=False)   #2*pi，即360度
#[0   1.04719755 2.0943951  3.14159265 4.1887902  5.23598776]

"""
numpy.concatenate((a1,a2,...),axis=0,out=None)
沿着现有的轴连接一串数组
a1,a2,...:除了与轴对应的维度（默认情况下为第一个）外，数组必须具有相同的形状
axis:数组将要连接的轴，默认值为0
out:存放返回值
"""
data=np.concatenate((data,[data[0]]))       #data的最后一行数据即对应angles“翻转一圈”后的0度
"""
data=[[0.4  0.32 0.35 0.3  0.3  0.88]
 [0.85 0.35 0.3  0.4  0.4  0.3 ]
 [0.43 0.89 0.3  0.28 0.22 0.3 ]
 [0.3  0.25 0.48 0.85 0.45 0.4 ]
 [0.2  0.38 0.87 0.45 0.32 0.28]
 [0.34 0.31 0.38 0.4  0.92 0.28]
 [0.4  0.32 0.35 0.3  0.3  0.88]]
 
 data[0]——numpy.ndarray
 [data[0]]——list
 data——numpy.ndarray
"""
angles=np.concatenate((angles,[angles[0]]))     #角度
#[0   1.04719755 2.0943951  3.14159265 4.1887902  5.23598776  0]

fig=plt.figure(facecolor="white")   #设置背景颜色
plt.subplot(111,polar=True)     #由“横纵坐标图”变成“雷达图”
"""
subplot(nrows,ncols,index,**kwargs)
返回给定网格位置的子图轴
如果nrows，ncols和index都小于10，它们也可以作为单个连接的三位数给出，
subplot(2,3,3)和subplot(233)都在当前窗口右上角创建了轴线，占据了
1/3的宽度和1/2的高度
polar:默认=False，判断子图是否是极坐标的投影
"""
plt.plot(angles,data,'o-',linewidth=1,alpha=0.2)    #alpha透明度
"""
plot(*args,**kwargs)
"""
plt.fill(angles,data,alpha=0.25)    #“横纵坐标与plot相同”（0 45 90 135 180 225 270 315 ）
"""
fill(*args,**kwargs)
通过提供多个x,y,[color]组绘制多个多边形,并填充
"""
plt.thetagrids(angles*180/np.pi,radar_labels,frac=1.2)  #“修正角度”；绕一圈圆周(0,60,120,180,240,300,0)
"""
thetagrids(*args,**kwargs)
在极坐标图中得到或设置网格线的theta位置
frac是极轴半径的一部分，标明标签的位置（(1 is the edge). e.g., 
1.05 is outside the axes and 0.95 is inside the axes.）
"""
plt.figtext(0.52,0.95,'霍兰德人格分析',ha='center',size=20)
"""
figtext(x,y,s,*args,**kwargs)
x,y:float，文本在坐标系中的位置
s:文本1
ha/horizontalalignment：{'center','right','left'}
size/fontsize
"""
legend=plt.legend(data_labels,loc=(0.94,0.80),labelspacing=0.1)
"""
legend(*args,**kwargs)
labelspacing:图例条目之间的垂直空间，以字体大小单位测量
"""
plt.setp(legend.get_texts(),fontsize='large')
"""
setp(*args,*kwargs)——getp
即set property
"""
plt.grid(True)  #网格呈现
#plt.savefig('holland_radar.jpg')        #保存输出图形
plt.show()

输出：