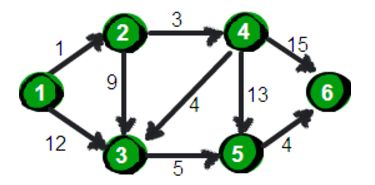
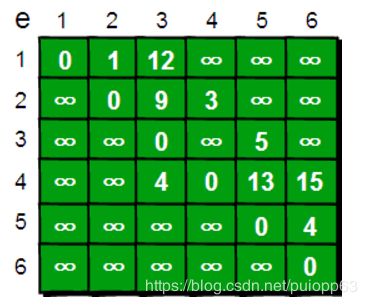
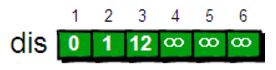
Dijkstra-迪杰斯特拉算法-理解(伪代码)(有向图 无向图)
迪杰斯特拉算法介绍
- 最短路径算法:用于计算一个节点到其他节点的最短路径。(一对多)
- 特点:是以起始点为中心向外层层扩展(?)
基本思想:
指定起点s,即从顶点s开始计算。
引进两个集合S和U。
S:记录已求出最短路径的顶点(以及相应的最短路径长度),
U:记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
-初始时,S中只有起点s;U中是除s之外的顶点。U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点v,并将其加入到S中。
-更新U中的顶点(及顶点对应的路径)。 然后,再从U中找出路径最短的顶点,并将其加入到S中。
... 重复该操作,直到遍历完所有顶点。
操作步骤
- 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"。例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞。
- 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
- 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
- 重复步骤(2)和(3),直到遍历完所有顶点
迪杰斯特拉算法图解(带权图)【下面的图是无向图】
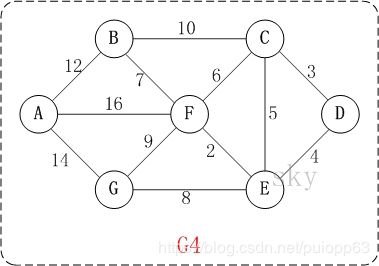
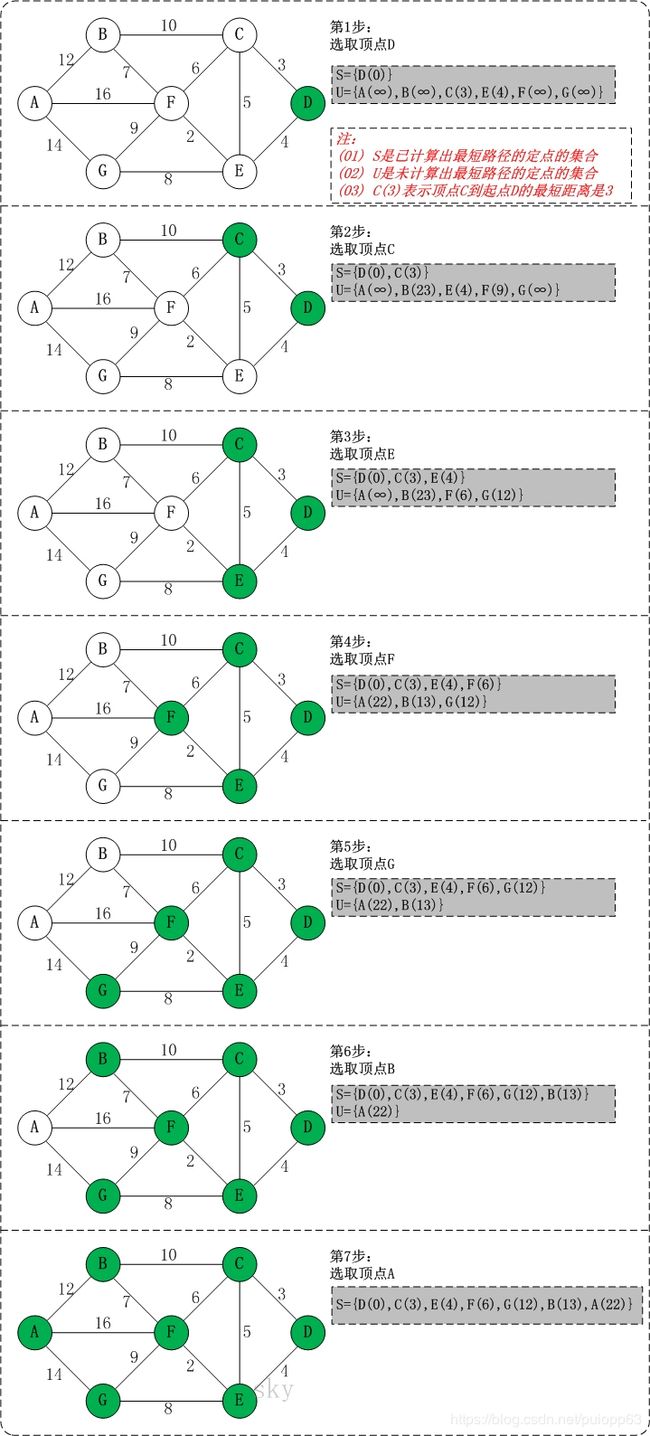
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
【这里体现的是(s,v)的距离可能大于(s,k)+(k,v)的距离,从而被修改】
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:
A(22) B(13) C(3) D(0) E(4) F(6) G(12)
const int infinity = 1000; //定义无穷常量,用1000表示
//定义图结构,采用邻接矩阵存储形式
template
class Graph
{
private:
/*邻接矩阵,对于有向网络(带权的有向图)其中存放的是权值*/
adjacent[max_size][max_size];
public:
void Dijkstra(int); //Dijkstra算法,求最短路径
};
void Graph::Dijkstra(int vertex)
{
//注意:下标表示结点
int count = 0; //用于记录访问过的结点数目,后面用于控制循环
bool find[max_size]; //用于标记已经找到最短路径的结点
int pre[max_size]; //用于存放当前结点的前驱结点的最短路径
int distance[max_size]; //用于存放当前结点的最短路径
//初始化在这里插入代码片
for(int i=0;i find[vertex] = true;
int v = vertex; //用来迭代顶点的变量
int d; //用来表示距离
while(count < max_size) //count用于记录访问过的次数
{
d = infinity;//开始置为无穷
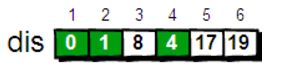
for(int i=0;i然后继续寻找剩下点(3,5,6)中的最小值,此处为3,也即确定了起点到点3的最近距离为distance[3]=8,然后更新其相邻点,结果为:
find[v] = true;//表示节点放到S中
//更新剩余的结点的前驱和最短距离
for(int i=0;i总结
代码:
1.二维矩阵代表了所有节点之间的关系,但只保存权重。
2.输入是矩阵的表,输出是指定的节点到其他顶点之间的最短路径。
input:adjacent[ m] [ m]
output:distance[m]