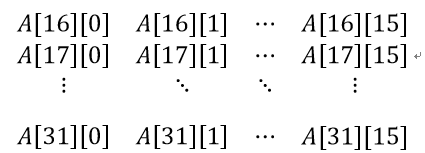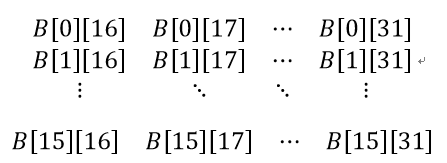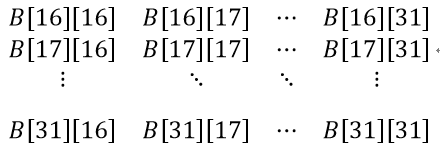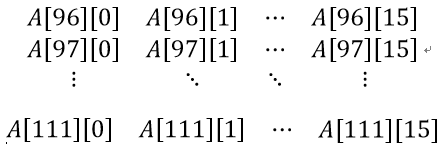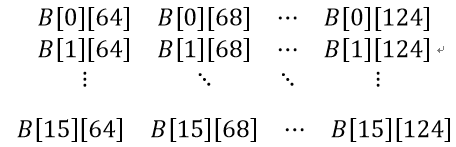关于《OPENCL异构并行计算》中矩阵乘法的分析

《OPENCL异构并行计算》中讲了如何利用OPENCL进行矩阵乘法运算，并给出了使用局部存储器优化、使用向量加载指令以及一个工作项同时计算多个输出的例子，这里对其进行简单分析：

同样，我们假设A矩阵（M×K）乘以B矩阵（K×N）得到C矩阵（M×N）,同时，M=N=K=2048。

1. 对于10.3节使用局部存储器优化

   分析代码清单10-5，他设置了子矩阵大小，和工作组大小BS为16x16,（工作组大小和BS大小应该一致）。

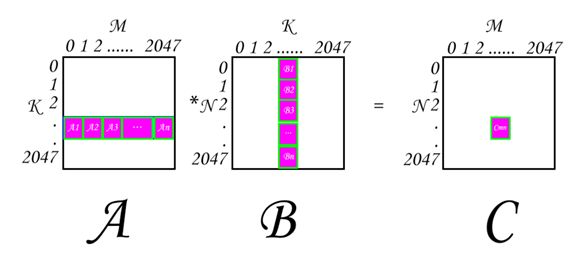
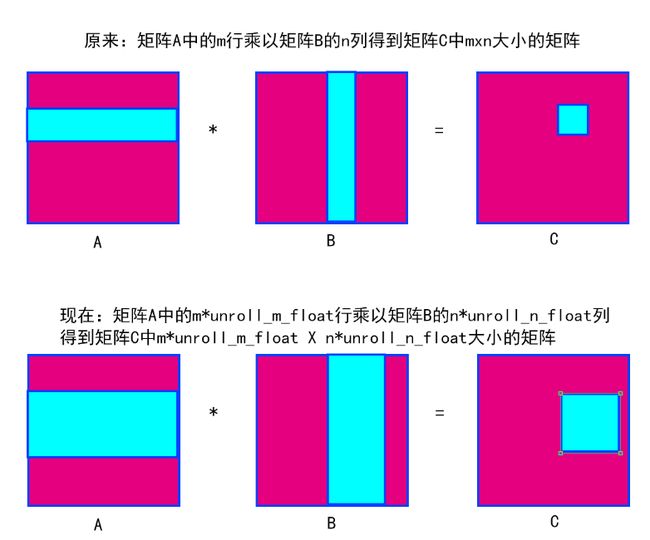
   这个代码的最终实现效果是如下图所示的计算：

   

   就是每次工作组循环，会把第i次的Ai和Bi用矩阵相乘的方法相乘，然后暂存到临时变量v中，然后整个工作组的计算结果就如下所示：A1*B1+A2*B2+…+An*Bn=Cmn，而一个工作组的大小为16X16，因此An中n=2048/16（M/BS） = 128。

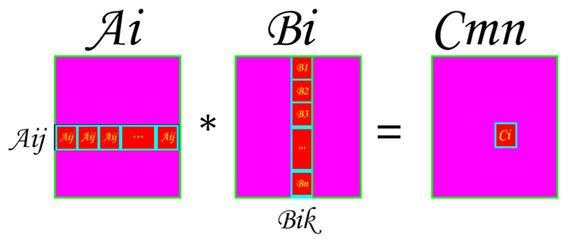
   要注意Ai和Bi，Cmn都是大小为BSXBS的矩阵，而每一个工作项是负责计算Ai矩阵的某一行Aij与Bi矩阵中的某一列Bik相乘，然后得到Cmn矩阵中的Cmni元素的，图示如下：

   

   即Ci是由Ai矩阵中的其中一行乘以Bi矩阵中的其中一列计算出来的，具体的行和列的值由工作项的局部id决定。

   首先说明，根据他的说法，AMD GPU每个工作组的局部存储器大小最大只有32KB，也就意味着我们在内核函数中定义的local变量大小不能超过32KB，那么他的代码用到local的地方只有ta数组和tb数组，而两个数组大小相同，类型相同，即两个数组的大小是相同的，一共是：2（两个数组）× sizeof(float) （数据类型大小）× BS（第一维大小） × BS（第二维大小） = 2× 4×16× 16 B = 2KB<32KB，满足要求。

   来看代码，我们首先看传入的参数：

   const global float *a, const global float *b, global float *c

   三个传入的一维数组分别代表的是A矩阵，B矩阵和输出的C矩阵，三个矩阵长度均为2048*2048，实际上就是把二维矩阵A[2048][2048]转换成了一位数组保存，同时A[0][0]代表A矩阵第一行第一个元素，注意，在行优先存储中，M行K列中第A[i][j]转换成一维数组的地址是a[i*K+j],记住是乘以K，也就是乘以列数，因为行优先存储代表一行的数据挨着，则第一行第一列数据挨着第一行第二列，第一行第三列……则第二行第一列的数据位置是1*总列数+1。举个例子，A矩阵第m行第n个元素A[m-1][n-1]的实际坐标为a[(m-1)*K+n-1]; B矩阵第m行第n个元素B[m-1][n-1]的实际坐标为b[(m-1)*N+n-1]; C矩阵第m行第n个元素C[m-1][n-1]的实际坐标为c[(m-1)*N+n-1]。

   再看函数体：

       int by = get_group_id(1);// 工作组第二维ID

       int bx = get_group_id(0);// 工作组第一维ID

       int tx = get_local_id(0);// 工作项的第一维局部ID

       int ty = get_local_id(1); // 工作项的第二维局部ID

   我们以by = 1,bx = 1,BS=16(工作组大小，在主机函数里面定义，-DBS=16并且localsize={16,16}来保证局部工作组大小和要计算的子矩阵块的大小相同)来分析这个代码：

   local float ta[BS][BS]; //ta数组来暂存A矩阵的子矩阵，大小为BSXBS，这里是16X16

   local float tb[BS][BS]; //tb数组来暂存A矩阵的子矩阵，大小为BSXBS，这里是16X16

   int ab = K*BS*by;//ab定义的是在A矩阵中，子块的行开始位置，对应于上图中的块A1矩阵中的第一个元素A1[0][0]在A矩阵的行坐标，拿以上的假设值举例，ab=2048*16*1，相对在A矩阵就是第17行第一个元素，即a[ab] ,即A[16][0]

   int ae = ab+K;//ae定义的是在A矩阵中，最后一个子块的行结束位置，对应于上图中的块An矩阵中最后一个元素的行坐标+1,拿以上的假设值举例，ab=2048*16 + 2048，相对在A矩阵就是第18行第一个元素，即a[ae],即A[17][0],就是行的结束位置，最终在循环里面-1，其实是代表了行的长度

   int bb = BS*bx; //bb定义的是在B矩阵中，子块的列开始位置，对应于上图中的块B1矩阵中的第一个元素B1[0][0]在B矩阵的列坐标, 拿以上的假设值举例，ab=16*1，相对在B矩阵就是第1行第17个元素，即b[bb],即B[0][16]

   float v = 0.0f;//v变量存储了每一个工作项的最终计算结果，也用作中间变量来存储每一次循环的计算结果

   然后来看循环：

   for(i = ab, j = bb; i < ae; i += BS, j += BS*N)

   首先，让i和j的值初始化成ab和bb，也就是初始化成A1块和B1块，然后每一次循环之后，i+=BS,j+=BS*N,即切换到A2块和B2块，直到An块和Bn块。

           ta[ty][tx] = a[i+ty*K+tx]; //code1

           tb[ty][tx] = b[j+ty*N+tx]; //code2

           barrier(CLK_LOCAL_MEM_FENCE);

   code1和code2是分别把全局存储器中A矩阵的子块Ai和b变量的子块Bj拷贝到局部存储器ta和tb的相应位置，然后用barrier等待所有工作项全部拷贝完再进行求和计算操作。例如，i=ab,j=bb的第一次循环，就是把A1矩阵和B1矩阵拷贝到局部空间ta和tb中了，又根据本体的举例的值，则ty=tx=0时，ta[0][0] = a[i] = A[16][0]; ty=0,tx=1时,ta[0][1]=a[i+1]=A[16][1]; ty=0,tx=1时，ta[1][0]=a[i+1*2048]=A[17][0];同理ta[1][1] = A[17][1],这个矩阵大小为BSxBS，则最后一个元素为ta[BS-1][BS-1]=ta[15][15]=a[i+15*2048+15]=A[31][15],即ta矩阵为：

   

   对于tb矩阵，同样计算过程，这里就不展开了，得到tb矩阵：

   

   接下来就是两个矩阵对应行和列（由工作项ty和tx决定）相乘，计算结果暂存到v中：

   for (int k = 0; k < BS; k++){

               v += ta[ty][k]*tb[k][tx];//code3

           }

   barrier(CLK_LOCAL_MEM_FENCE);

   注意需要barrier，不然会出现有的工作项还没计算完，ta和tb的值就被下一次循环改了而得不到正确的结果。

   那么进入第二次循环，即i=ab+BS=ab+16,j=bb+BS*N=bb+16*2048,此时再次计算ta和tb的值，就会发现此时ta存的是上图A2的值，tb存的是上图B2的值，即ta为：

   

   tb为：

   

   ，然后工作项v刚才存的是A1*B1的值，现在继续计算存A2*B2的值，直到An*Bn的值，最后把他存放在Cmn中：

   c[BS*N*by + bx*BS + ty*N + tx] = v;//code4

   BS*N*by确定大块的行偏移，bx*BS确定大块的列偏移，ty*N确定子块里面的列偏移，tx确定子块里面的行偏移。

   即完成了局部存储器优化的存储操作，但还不够好，因为我们没有使用向量优化，接下来看向量优化。

2. 对于10.4节使用向量加载指令

   这里的local变量大小一共是：2（两个数组）× sizeof(float4) （数据类型大小）× BS（第一维大小） × BS（第二维大小） = 2× 16×16× 16 B = 8KB<32KB，满足要求。

   这段代码说明了如何使用向量来进行优化，使得一个工作项计算了16个结果而不是1个，他的方法如下：

   首先，他把B矩阵由原来的一维float数组转换成了一维float4数组，则有必要说明B矩阵现在存了些什么东西。

   我们都知道B矩阵大小为2048*2048，也是b数组的大小，而用float4优化之后b数组大小变成了（2048/4）*2048=512*2048,float4的四个分量xyzw值分别是如图所示：

   b.x

   b.y

   b.z

   b.w

   然后分析代码：

       local float4 ta[BS][BS];

       local float4 tb[BS][BS];

   这里把ta和tb转换成了float4类型，能够分别存下A矩阵和B矩阵的整整四块矩阵。

   int ab = 4*K*BS*by;

   int ae = ab+K;

   int bb = BS*bx;

   ab在原来的基础上乘了4，是因为由于本代码实现了一个工作组的计算范围在行范围和列范围各扩展了4倍，即原来每次计算是用的A矩阵的连续m行和B矩阵的连续n列计算出了mxn的结果C矩阵，现在每次计算就用了A矩阵的连续4*m行和b矩阵的连续4*n列计算出了4*m*4*n = 16*m*n块的结果C矩阵，因此由于ab变量被定义为子块的行开始坐标，那么因为上一个工作组已经计算了原来四倍的行数，所以他的位置乘了4。ae不变，是因为永远要计算到头，也就是A1到An。

   而对于bb，看似跟原来比没有任何改变，其实不然，实际上仍然乘了四倍，原因很简单，就是b矩阵换成了float4来存储，所以举例来说原来对于索引位置1,即b[1]存储的是B[0][1]的值，而现在，根据上面四个图我们可以看到，他存储的值分别是x：B[0][4],y: B[0][5],z: B[0][6],w: B[0][7]。实际上还是翻了四倍。

   接下来：

   float4 v[4];

   for(int ii = 0; ii < 4; ii++) {

   v[ii] = 0.0f;

   }

   定义float4数组v，注意v数组有四个元素，而每个元素又都是float4，即最终值的个数实际上是16个。

   const int N_float4 = N/4;

   把索引除以4以便按上次的索引位置来访问b数组的值。

   for(i = ab, j = bb; i < ae; i += BS, j += BS*N_float4)

   仍然是一大块一大块的相乘然后相加，不做解释。

   float4 temp;

   temp.x = a[0*BS*K + i+ty*K+tx]; //code1

   temp.y = a[1*BS*K + i+ty*K+tx]; //code1

   temp.z = a[2*BS*K + i+ty*K+tx]; //code1

   temp.w = a[3*BS*K + i+ty*K+tx]; //code1

   ta[ty][tx] = temp;

   这四句定义了ta数组存储的内容，经过如第一部分一样的手动计算，得到第一次循环ta数组的四个值分别为：

   ta.x

   ta.y

   ta.z

   ta.w

   可以发现其实ta存储的是连续的64行到127行的前15列元素。

   然后tb：

   tb[ty][tx] = b[j+ty*N_float4+tx]; //code2

   计算可知tb存储的是以下内容：

   tb.x

   tb.y

   tb.z

   tb.w

    

   然后计算：

   for (int k = 0; k < BS; k++){

               v[0] += ta[ty][k].x*tb[k][tx];//code3

               v[1] += ta[ty][k].y*tb[k][tx];//code3

               v[2] += ta[ty][k].z*tb[k][tx];//code3

               v[3] += ta[ty][k].w*tb[k][tx];//code3

           }

           barrier(CLK_LOCAL_MEM_FENCE);

   注意，由于v[0]到v[3]都是float4，实际上for里面的四行代码得到的是16个结果，例如ta[0][0].x * tb[0][0],这里ta[0][0].x是一个float，根据上图值为A[64][0]，而tb[0][0]有四个分量，分别是B[0][64],B[0][65],B[0][66],B[0][67],实际上这一次for循环下来，但这一句就计算了A矩阵的第65行与B矩阵的65,66,67,68行计算的结果，并把它存入了C[64][64],C[64][65],C[64][66],C[64][67]中，实际上tx=0,ty=0的工作项计算的结果有16个，由A[64][0]与B[0][64],B[0][65],B[0][66],B[0][67]得到的C[64][64],C[64][65],C[64][66],C[64][67]；由A[80][0]与B[0][64],B[0][65],B[0][66],B[0][67]得到的C[80][64],C[80][65],C[80][66],C[80][67]；由A[96][0]与B[0][64],B[0][65],B[0][66],B[0][67]得到的C[96][64],C[96][65],C[96][66],C[96][67]；由A[112][0]与B[0][64],B[0][65],B[0][66],B[0][67]得到的C[112][64],C[112][65],C[112][66],C[112][67]；以此类推，所有的值都是这样算出来的。

   即最终的v矩阵是：

   

   以下是个整个过程一个工作组的示例图：

ta.x

ta.y

ta.z

ta.w

ta矩阵

乘以下面的tb矩阵

tb[0].x

tb[0].y

tb[0].z

tb[0].w

tb[1].x

tb[1].y

tb[1].z

tb[1].w

……

tb[15].x

tb[15].y

tb[15].z

tb[15].w

tb矩阵

得到V矩阵：

V[0] （ta.x顺次得到）

V[1]

V[2]

V[3]

其中每一个V[i]中，包括：

V[i]:

xyzw

xyzw

……

xyzw

 

 

1. 对于10.5节一个工作项计算多个输出

   这个就在上一个的基础上加了多个块，在M上乘了unroll_m_float4倍，在N上乘了unroll_n_float4倍，示意图如下，代码不细讲，一看就懂。

   注意，这里的local变量大小是：unroll_m_float4×unroll_n_float4 ×2（两个数组）× sizeof(float) （数据类型大小）× BS（第一维大小） × BS（第二维大小） = unroll_m_float4×unroll_n_float4 ×2× 16×16× 16 B = unroll_m_float4×unroll_n_float4 ×8KB应该小于32KB，则unroll_m_float4×unroll_n_float4应该小于等于4。根据书中的例子，unroll_m_float4×unroll_n_float4=2。