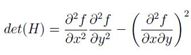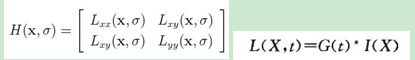SIFT、SURF、Harris、BRIEF、FAST、DAISY、FAST等描述符介绍

本博文下载链接：http://pan.baidu.com/s/1i5tCo1f

局部图像特征描述是计算机视觉的一个基本研究问题，在寻找图像中的对应点以及物体特征描述中有着重要的作用。它是许多方法的基础，因此也是目前视觉研究中的一个热点，每年在视觉领域的顶级会议ICCV/CVPR/ECCV上都有高质量的特征描述论文发表。同时它也有着广泛的应用，举例来说，在利用多幅二维图像进行三维重建、恢复场景三维结构的应用中，其基本出发点是要有一个可靠的图像对应点集合，而自动地建立图像之间点与点之间的可靠对应关系通常都依赖于一个优秀的局部图像特征描述子。又比如，在物体识别中，目前非常流行以及切实可行的方法之一是基于局部特征的，由于特征的局部性，使得物体识别可以处理遮挡、复杂背景等比较复杂的情况。

局部图像特征描述的核心问题是不变性（鲁棒性）和可区分性。由于使用局部图像特征描述子的时候，通常是为了鲁棒地处理各种图像变换的情况。因此，在构建/设计特征描述子的时候，不变性问题就是首先需要考虑的问题。在宽基线匹配中，需要考虑特征描述子对于视角变化的不变性、对尺度变化的不变性、对旋转变化的不变性等；在形状识别和物体检索中，需要考虑特征描述子对形状的不变性。

然而，特征描述子的可区分性的强弱往往和其不变性是矛盾的，也就是说，一个具有众多不变性的特征描述子，它区分局部图像内容的能力就稍弱；而如果一个非常容易区分不同局部图像内容的特征描述子，它的鲁棒性往往比较低。举个例子，假定我们需要对一个点周围固定大小的局部图像内容进行描述。如果我们直接将图像内容展开成一个列向量对其进行描述，那么只要局部图像内容发生了一点变化，就会使得它的特征描述子发生较大的变化，因此这样的特征描述方式很容易区分不同的局部图像内容，但是对于相同的局部图像内容发生旋转变化等情况，它同样会产生很大的差异，即不变性弱。

而另一方面，如果我们通过统计局部图像灰度直方图来进行特征描述，这种描述方式具有较强的不变性，对于局部图像内容发生旋转变化等情况比较鲁棒，但是区分能力较弱，例如无法区分两个灰度直方图相同但内容不同的局部图像块。

综上所述，一个优秀的特征描述子不仅应该具有很强不变性，还应该具有很强的可区分性。在诸多的局部图像特征描述子中，SIFT（ScaleInvariant Feature Transform）是其中应用最广的，它在1999年D. Lowe首次提出，至2004年得到完善。SIFT的提出也是局部图像特征描述子研究领域一项里程碑式的工作。由于SIFT对尺度、旋转以及一定视角和光照变化等图像变化都具有不变性，并且SIFT具有很强的可区分性，自它提出以来，很快在物体识别、宽基线图像匹配、三维重建、图像检索中得到了应用，局部图像特征描述子在计算机视觉领域内也得到了更加广泛的关注，涌现了一大批各具特色的局部图像特征描述子。
SURF（SpeededUp Robust Features）是对SIFT的改进版本，它利用Haar小波来近似SIFT方法中的梯度操作，同时利用积分图技术进行快速计算，SURF的速度是SIFT的3-7倍，大部分情况下它和SIFT的性能相当，因此它在很多应用中得到了应用，尤其是对运行时间要求高的场合。
DAISY是面向稠密特征提取的可快速计算的局部图像特征描述子，它本质思想和SIFT是一样的：分块统计梯度方向直方图，不同的是，DAISY在分块策略上进行了改进，利用高斯卷积来进行梯度方向直方图的分块汇聚，这样利用高斯卷积的可快速计算性就可以快速稠密地进行特征描述子的提取。比较巧合的是，DAISY这种特征汇聚策略被一些研究者（Matthen Brown，Gang Hua，Simon Winder）通过机器学习的方法证明相对于其他几种特征汇聚策略（卡迪尔坐标下分块、极坐标下分块）是最优的。
BRIEF（BinaryRobust Independent Element Feature）利用局部图像邻域内随机点对的灰度大小关系来建立局部图像特征描述子，得到的二值特征描述子不仅匹配速度快，而且存储要求内存低，因此手机应用中具有很好的应用前景。其实，利用邻域内点对的灰度大小关系进行特征描述这一思想在SMD（ECCV’08）中就已经有了。除了BRIEF，近两年还提出了许多二值特征描述子，例如ORB、BRISK、FREAK。上述这些特征描述子都是基于手动设计得到的。下面就具体的梳理一下SIFT、SURF、DAISY、FAST 、BRIEF、ORB、HARRIS。

SIFT

SIFT（Scale-invariantfeature transform）是一种检测局部特征的算法，该算法通过求一幅图中的特征点（interestpoints,or corner points）及其有关scale 和 orientation 的描述子得到特征并进行图像特征点匹配。

SIFT算法的实质：是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。

SIFT特征不只具有尺度不变性，即使改变旋转角度，图像亮度或拍摄视角，仍然能够得到好的检测效果。整个算法分为以下几个部分：

SIFT特征提取算法流程：

1、 输入图像

2、 多尺度空间极值点检测

3、 关键点的精确定位

4、 关键点的主方向计算

5、  描述子的构造

6、 特征向量

SIFT的特征描述的构造和匹配过程，由于篇幅原因，具体的可以见另外一篇博客，写的很仔细：

SIFT介绍

局部特征提取算法-SIFT的性质:

　　•SIFT算法由D.G.Lowe 1999年提出，2004年完善总结。后来Y.Ke将其描述子部分用PCA代替直方图的方式，对其进行改进。

 　　•SIFT算法是一种提取局部特征的算法，在尺度空间寻找极值点，提取位置，尺度，旋转不变量

　　•SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性。

　　•独特性好，信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配。

　　•多量性，即使少数的几个物体也可以产生大量SIFT特征向量。

　　•可扩展性，可以很方便的与其他形式的特征向量进行联合。

SURF

Surf算法是对Sift算法的一种改进，主要是在算法的执行效率上比Sift算法来讲运行更快！

SURF算法对积分图像进行操作，卷积只和前一幅图像有关，其降采样的方法是申请增加图像核的尺寸，这也是SIFT算法与SURF算法在使用金字塔原理方面的不同。SURF算法允许尺度空间多层图像同时被处理，不需对图像进行二次抽样，从而提高算法性能。

算法原理：

(1)、构建Hessian矩阵

Hessian矩阵是Surf算法的核心，为了方便运算，假设函数f(z，y)，Hessian矩阵H是由函数，偏导数组成：

H矩阵判别式为：

判别式的值是H矩阵的特征值，可以利用判定结果的符号将所有点分类，根据判别式取值正负，来判别该点是或不是极值点。在SURF算法中，用图像像素l(x，y)代替函数值f(x，y)，选用二阶标准高斯函数作为滤波器，通过特定核间的卷积计算二阶偏导数，这样便能计算出H矩阵的三个矩阵元素的值，从而计算出H矩阵：

L (X，t)是一幅图像在不同解析度下的表示，可以利用高斯核G(t)与图像函数I(x)卷积实现。通过这种方法可以为图像中每个像素计算出其H行列式的值，并用这个值来判别特征点。为方便应用，Herbert Bay提出用近似值现代替L。为平衡准确值与近似值间的误差引入随尺度变化的权值，则H矩阵判别式可表示为：

(2)、构建尺度空间

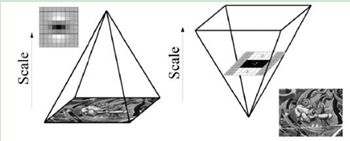
图像的尺度空间L（x，t）是这幅图像在不同解析度（Scale）下的表示。在计算视觉领域，尺度空间被象征性的表述为一个图像金字塔，其中，输入图像函数反复与高斯函数的核卷积并反复对其进行二次抽样，这种方法主要用于Sift算法的实现，但每层图像依赖于前一层图像，并且图像需要重设尺寸，因此，这种计算方法运算量较大，而SURF算法申请增加图像核的尺寸，这也是SIFT算法与SURF算法在使用金字塔原理方面的不同。算法允许尺度空间多层图像同时被处理，不需对图像进行二次抽样，从而提高算法性能。下左图是传统方式建立的一个金字塔结构，图像的尺寸是变化的，并且运算会反复使用高斯函数对子层进行平滑处理，右图Surf算法使原始图像保持不变而只改变滤波器大小。

(3)、精确定位特征点

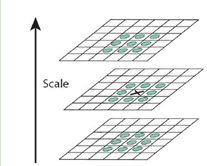
　　此步骤和sift类似，将经过hessian矩阵处理过的每个像素点与其3维领域的26个点进行大小比较，如果它是这26个点中的最大值或者最小值，则保留下来，当做初步的特征点。采用3维线性插值法得到亚像素级的特征点，同时也去掉那些值小于一定阈值的点。

(4)、主方向确定

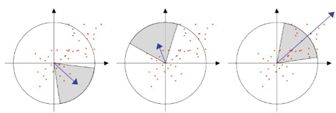
Sift选取特征点主方向是采用在特征点领域内统计其梯度直方图，取直方图bin值最大的以及超过最大bin值80%的那些方向做为特征点的主方向。而在surf中，不统计其梯度直方图，而是统计特征点领域内的harr小波特征。即在特征点的领域(比如说，半径为6s的圆内，s为该点所在的尺度)内，统计60度扇形内所有点的水平haar小波特征和垂直haar小波特征总和，haar小波的尺寸变长为4s，这样一个扇形得到了一个值。然后60度扇形以一定间隔进行旋转，最后将最大值那个扇形的方向作为该特征点的主方向。该过程的示意图如下：

(5)特征点描述子生成

sift中，是在特征点周围取16*16的邻域，并把该领域化为4*4个的小区域，每个小区域统计8个方向梯度，最后得到4*4*8=128维的向量，该向量作为该点的sift描述子。

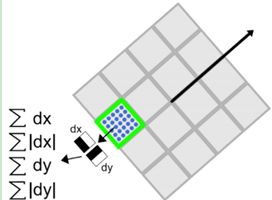
在surf中，也是在特征点周围取一个正方形框，框的边长为20s(s是所检测到该特征点所在的尺度)。该框带方向，方向当然就是第4步检测出来的主方向了。然后把该框分为16个子区域，每个子区域统计25个像素的水平方向和垂直方向的haar小波特征，这里的水平和垂直方向都是相对主方向而言的。该haar小波特征为水平方向值之和，水平方向绝对值之和，垂直方向之和，垂直方向绝对值之和。该过程的示意图如下所示：

这样每个小区域就有4个值，所以每个特征点就是16*4=64维的向量, 相比sift而言，少了一半，这在特征匹配过程中会大大加快匹配速度。

总结：

Sift/Surf采用Henssian矩阵获取图像局部最值还是十分稳定的，但是在求主方向阶段太过于依赖局部区域像素的梯度方向，有可能使得找到的主方向不准确，后面的特征向量提取以及匹配都严重依赖于主方向，即使不大偏差角度也可以造成后面特征匹配的放大误差，从而匹配不成功；另外图像金字塔的层取得不足够紧密也会使得尺度有误差，后面的特征向量提取同样依赖相应的尺度，发明者在这个问题上的折中解决方法是取适量的层然后进行插值。Sift是一种只利用到灰度性质的算法，忽略了色彩信息。

SURF和SIFT的主要区别：

1） 预处理时：SITF将图像在各个方向上扩大了两倍，SURF则是计算积分图像。

2） 尺度空间的构造：SIFT是用高斯卷积乘以图像，获得LoG空间。通过相邻层相减得到DoG尺度空间，对原图进行向下采样得到下一层；SURF通过改变Box滤波器的尺寸来得到不同的尺度空间，无需改变图像的大小。

3） 极值点的确定：SIFT通过比较DoG尺度空间3维（3*3*3）像素灰度值来确定极值；SURF用Hessian矩阵行列式的特征值符号来确定极值。

4） 是否需要剔除边缘响应：SIFT需要，根据Hessian的求出主曲率，采用阈值抑制掉边缘响应；而SURF不需要剔出边缘响应；

5） 极值点方向估计：SIFT根据像素的梯度来确定。将360°分成36份，进行直方图统计；SURF根据像素在x,y方向上的Harr小波响应来确定。将360°分成72份，用直方图统计每相邻60°之内的响应值之和。

6） 特征向量维数：SIFT是4*4个子区域，8个方向共128维；SURF是4*4个子区域，4个方向的响应值共64维；

7） 相似度度量方法：基于KD的存储结构，采用BBF算法进行匹配；SURF是快速索引匹配和欧式距离差方匹配；

8） 剔除伪匹配点：SIFT采用RANSAC算法剔除伪匹配点；SURF则不需要剔除伪匹配点；

Harris角点

基本原理：人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。

角点定义：窗口向任意方向的移动都导致图像灰度的明显变化。

如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点；如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么，窗口内的图像可能就是一条直线的线段。

平坦区域（左）：任意方向移动，无灰度变化

边缘（中）：沿着边缘方向移动，无灰度变化

角点（右）：沿任意方向移动，明显灰度变化

FAST 

前面已经介绍了很多图像特征检测算子，我们可以用LoG或者DoG检测图像中的Blobs（斑点检测），可以根据图像局部的自相关函数来求得Harris角点（Harris角点），后面又提到了两种十分优秀的特征点及它们的描述方法SIFT特征与SURF特征。SURF特征算是为了提高运算效率对SIFT特征的一种近似，虽然在有些实验环境中已经达到了实时，但是我们实践工程应用中，特征点的提取与匹配只是整个应用算法中的一部分，所以我们对于特征点的提取必须有更高的要求，从这一点来看前面介绍的的那些特征点方法都不可取。

      为了解决这个问题，Edward Rosten和Tom Drummond在2006年发表的“Machine learning for high-speed corner detection”文章中提出了一种FAST特征，并在2010年对这篇论文作了小幅度的修改后重新发表。FAST的全称为Features From Accelerated Segment Test。Rosten等人将FAST角点定义为：若某像素点与其周围领域内足够多的像素点处于不同的区域，则该像素点可能为角点。也就是某些属性与众不同，考虑灰度图像，即若该点的灰度值比其周围领域内足够多的像素点的灰度值大或者小，则该点可能为角点。(FAST主要用于角点检测)

算法步骤：

（1）从图片中选取一个像素P，下面我们将判断它是否是一个特征点。我们首先把它的亮度值设为Ip。

（2）设定一个合适的阈值t。

（3）考虑以该像素点为中心的一个半径为3像素的离散化的Bresenham圆，则圆边界上有16个像素。

（4）现在，如果在这个大小为16个像素的圆上有n个连续的像素点，它们的像素值要么都比Ip+t大，要么都比Ip−t小，那么它就是一个角点。n的值可以设置为12或者9，实验证明选择9可能会有更好的效果。

上面的算法中，对于图像中的每一个点，我们都要去遍历其邻域圆上的16个点的像素，效率较低。我们下面提出了一种高效的测试（high-speed test）来快速排除一大部分非角点的像素。该方法仅仅检查在位置1，9，5和13四个位置的像素，首先检测位置1和位置9，如果它们都比阈值暗或比阈值亮，再检测位置5和位置13。如果P是一个角点，那么上述四个像素点中至少有3个应该必须都大于Ip+t或者小于Ip−t，因为若是一个角点，超过四分之三圆的部分应该满足判断条件。如果不满足，那么p不可能是一个角点。对于所有点做上面这一部分初步的检测后，符合条件的将成为候选的角点，我们再对候选的角点，做完整的测试，即检测圆上的所有点。

简单的说：FAST特征检测算法定义基于特征点周围的图像灰度值，检测候选特征点周围一圈的像素值，如果候选点周围领域内有足够多的像素点与该候选点的灰度值差别够大，则认为该候选点为一个特征点。为了获得更快的结果，还采用了额外的加速办法，如果测试了候选点周围每隔90°角的4个点，应该至少有3个和候选点的灰度值差足够大，否则则不用再计算其他点，直接认为该候选点不是特征点。候选点周围的圆的选取半径是一个很重要的参数，这里我为了简单高效，采用半径为3，共有16个周边像素需要比较。

BRIEF

我们已经知道SIFT特征采用了128维的特征描述子，由于描述子用的浮点数，所以它将会占用512 bytes的空间。类似地，对于SURF特征，常见的是64维的描述子，它也将占用256bytes的空间。如果一幅图像中有1000个特征点（不要惊讶，这是很正常的事），那么SIFT或SURF特征描述子将占用大量的内存空间，对于那些资源紧张的应用，尤其是嵌入式的应用，这样的特征描述子显然是不可行的。而且，越占有越大的空间，意味着越长的匹配时间。 但是实际上SFIT或SURF的特征描述子中，并不是所有维都在匹配中有着实质性的作用。我们可以用PCA、LDA等特征降维的方法来压缩特征描述子的维度。还有一些算法，例如LSH，将SIFT的特征描述子转换为一个二值的码串，然后这个码串用汉明距离进行特征点之间的匹配。这种方法将大大提高特征之间的匹配，因为汉明距离的计算可以用异或操作然后计算二进制位数来实现，在现代计算机结构中很方便。下面来们提取一种二值码串的特征描述子。

 BRIEF提供了一种计算二值串的捷径，而并不需要去计算一个类似于SIFT的特征描述子。它需要先平滑图像，然后在特征点周围选择一个Patch，在这个Patch内通过一种选定的方法来挑选出来n_d个点对。然后对于每一个点对(p,q)，我们来比较这两个点的亮度值，如果I(p)>I(q)，则这个点对生成了二值串中一个的值为1，如果I(p)d个点对，都进行比较之间，我们就生成了一个n_d长的二进制串。

 对于n_d的选择，我们可以设置为128, 256或512, 这三种参数在OpenCV中都有提供，但是OpenCV中默认的参数是256，这种情况下，非匹配点的汉明距离呈现均值为128比特征的高斯分布。一旦维数选定了，我们就可以用汉明距离来匹配这些描述子了。值得注意的是，对于BRIEF，它仅仅是一种特征描述符，它不提供提取特征点的方法。所以，如果你必须使一种特征点定位的方法，如FAST、SIFT、SURF等。总体来说，BRIEF是一个效率很高的提取特征描述子的方法，同时，当图像发生很大的平面内的旋转,它有着很好的识别率。

 

还有DAISY和ORB后面再补充介绍；

 

其中：SIFT、SURF、Harris、DAISY都属于角点的检测方法；

引用：

[1]“局部图像特征描述概述”中国科学院自动化研究所 模式识别国家重点实验室   樊彬

[2] http://www.cnblogs.com/ronny/p/4078710.html

[3] http://www.cnblogs.com/ronny/p/4081362.html?utm_source=tuicool&utm_medium=referral

[4] http://www.cnblogs.com/ronny/p/4083537.html

[5] http://www.cnblogs.com/ronny/p/4009425.html?utm_source=tuicool&utm_medium=referral

[6]http://wenku.baidu.com/link?url=2C37qVQPMUMnGG6FcTiidI6xPEbkRmFPC5gNltDgDSeBfSbq8JytCxJvOe6qyNk0ZgbVs_cRGpol25FU9Sac2P5Ffp8h9RnMPKBA_ezn3t_