numpy手写softmax回归
softmax诞生原因
线性回归主要用于连续值预测,即回归问题,比如判定一个东西是鸡的概率是多少
而当模型需要预测多个离散值时,即分类问题,比如判定一个东西是鸡还是鹅还是鸭
此时就需要多个输出单元,并且修改运算方式从而方便预测和训练,这也就是softmax层诞生的原因
这里使用的是minist手写数字识别数据集
1.首先通过Pytorch读取数据集
def load_data():
train_dataset = datasets.MNIST(root='./data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = datasets.MNIST(root='./data/',
transform=transforms.ToTensor(),
train=False)
# Data Loader (Input Pipeline)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
return train_loader,test_loader
2.softmax回归模型
这里每个输入都是 28 ∗ 28 28*28 28∗28的数据,即 784 ∗ 1 784*1 784∗1
这里我选择每次都输入batch_size为64的数据进行优化
即输入数据shape为(64,784)
softmax和线性回归一样都是对将输入特征用线性函数计算输出值,但是这里有一点不同,就是softmax回归的输出值个数不再是一个,而是等于类别数,这里输出类别为0123456789十个数字,因此有十个输出值
因此此时需要十个线性函数来对应这十个输入值到输出值的转化
y 1 = W 1 , 1 ∗ x 1 + W 2 , 1 ∗ x 2 + . . . + W 783 , 1 ∗ x 783 , 1 + W 784 , 1 ∗ x 784 , 1 + b 1 y 2 = W 1 , 2 ∗ x 1 + W 2 , 2 ∗ x 2 + . . . + W 783 , 2 ∗ x 783 , 2 + W 784 , 2 ∗ x 784 , 2 + b 2 . . . . . . y 10 = W 1 , 10 ∗ x 1 + W 2 , 10 ∗ x 2 + . . . + W 783 , 10 ∗ x 783 , 10 + W 784 , 10 ∗ x 784 , 10 + b 10 y_1=W_{1,1}*x_1+W_{2,1}*x_2+...+W_{783,1}*x_{783,1}+W_{784,1}*x_{784,1}+b_{1}\\ y_2=W_{1,2}*x_1+W_{2,2}*x_2+...+W_{783,2}*x_{783,2}+W_{784,2}*x_{784,2}+b_{2}\\ ...\\ ...\\ y_{10}=W_{1,10}*x_1+W_{2,10}*x_2+...+W_{783,10}*x_{783,10}+W_{784,10}*x_{784,10}+b_{10} y1=W1,1∗x1+W2,1∗x2+...+W783,1∗x783,1+W784,1∗x784,1+b1y2=W1,2∗x1+W2,2∗x2+...+W783,2∗x783,2+W784,2∗x784,2+b2......y10=W1,10∗x1+W2,10∗x2+...+W783,10∗x783,10+W784,10∗x784,10+b10
其中w矩阵为(784,10),即

b矩阵为(64,10)
即
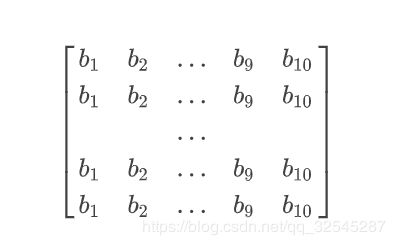
最终为

y矩阵最终等于 x ( 64 , 784 ) ∗ w ( 784 , 10 ) + b ( 64 , 10 ) x(64,784)*w(784,10)+b(64,10) x(64,784)∗w(784,10)+b(64,10)
其中 x ( 64 , 784 ) ∗ w ( 784 , 10 ) x(64,784)*w(784,10) x(64,784)∗w(784,10)结果为 ( 64 , 10 ) (64,10) (64,10),加上b最后还是一个 ( 64 , 10 ) (64,10) (64,10)的矩阵
对应一个批次64个数据中中,预测十个数字每个数字的可能性大小
代码如下
def train():
w=np.random.randn(784,10) #生成随机正太分布的w矩阵
b=np.zeros((64,10)) #生成全是0的b矩阵
for batch_idx, (data, target) in enumerate(train_loader):
data= np.squeeze(data.numpy()).reshape(64,28*28)
# 把张量中维度为1的维度去掉,并且改变维度为(64,784)
target = target.numpy() #x矩阵 (64,784)
y_hat=np.dot(data,w)+b
print(y_hat.shape)
最终y_hat为 ( 64 , 10 ) (64,10) (64,10)
3.softmax运算
假设预测值分别是1,10,…100,此时直接通过输出值判断, y 10 y_{10} y10最大识别结果为数字9
但是这样会使得,不知道怎么划分这些值到底是很大还是很小,也就是难以去优化参数
比如如果这次里100最大,但是下次中10000最大而且最小的都有1000,那么100到底算不算大
这里就用softmax运算来解决
y 1 ^ , y 2 ^ . . . y 10 ^ = s o f t m a x ( o u t p u t 1 , o u t p u t 2 . . . o u t p u t 10 ) 其 中 y j ^ = e x p ( o u t p u t j ) ∑ i = 1 10 e x p ( o u t p u t i ) \hat{y_1},\hat{y_2}...\hat{y_{10}}=softmax(output_1,output_2...output_{10})\\ 其中\\ \hat{y_j}=\frac{exp(output_j)}{\sum_{i=1}^{10}{exp(output_i)}} y1^,y2^...y10^=softmax(output1,output2...output10)其中yj^=∑i=110exp(outputi)exp(outputj)
即每个 y i ^ \hat{y_i} yi^为exp(当前输出值)/所有exp(输出值)求和
这样一来,最终所有 y i ^ \hat{y_i} yi^的和为1,而且每个 y i ^ \hat{y_i} yi^对应的都是对每个手写数字概率的预测
def softmax(label):
#label时一个(64,10)的numpy数组
label = np.exp(label.T)#先把每个元素都进行exp运算
sum = label.sum(axis=0) #对于每一行进行求和操作
# print((label/sum).T.shape)
# print((label/sum).T)
return (label/sum).T #通过广播机制,使每行分别除以各种的和
4.交叉熵损失函数
这里的损失函数我们可以直接采用平方损失函数,即 ( y i ^ − y ) 2 (\hat{y_i}-y)^2 (yi^−y)2
但是想要预测结果正确,我们不需要使得预测值和实际值完全一致
只需要这个 y i ^ \hat{y_i} yi^的预测值比其他的都大即可,而平方损失则过于严格
我们可以采用交叉熵作为损失函数
对于单个的训练样本而言,交叉熵为
− ∑ i = 1 输 出 单 元 数 第 i 个 实 际 值 ∗ l o g ( 第 i 个 预 测 值 ) 即 − ∑ i = 1 10 y i l o g ( y ^ i ) -\sum_{i=1}^{输出单元数}第i个实际值*log(第i个预测值)\\ 即\\ -\sum_{i=1}^{10}yilog(\hat{y}_i) −i=1∑输出单元数第i个实际值∗log(第i个预测值)即−i=1∑10yilog(y^i)
此时对于一个训练批次而言,损失函数为
L o s s = − 1 b a t c h s i z e ∑ j = 1 b a t c h s i z e ∑ i = 1 输 出 单 元 数 y i l o g ( y ^ i ) Loss=-\frac{1}{batchsize}\sum_{j=1}^{batchsize}{\sum_{i=1}^{输出单元数}yilog(\hat{y}_i)} Loss=−batchsize1j=1∑batchsizei=1∑输出单元数yilog(y^i)
这里就是
L o s s = − 1 64 ∑ j = 1 64 ∑ i = 1 10 y i l o g ( y ^ i ) Loss=-\frac{1}{64}\sum_{j=1}^{64}{\sum_{i=1}^{10}yilog(\hat{y}_i)} Loss=−641j=1∑64i=1∑10yilog(y^i)
然而实际上 y 1 , y 2 . . . y 10 y_1,y_2...y_{10} y1,y2...y10这10个实际值只会有一个是1,其他全是0,也就是说,式子变成了
L o s s = − 1 64 ∑ j = 1 64 l o g ( y ^ i ) Loss=-\frac{1}{64}\sum_{j=1}^{64}{log(\hat{y}_i)} Loss=−641j=1∑64log(y^i)
然后再结合模型
o u t p u t i = W 1 , i ∗ x 1 + W 2 , i ∗ x 2 + . . . + W 783 , i ∗ x 783 , i + W 784 , i ∗ x 784 , i + b i output_i=W_{1,i}*x_1+W_{2,i}*x_2+...+W_{783,i}*x_{783,i}+W_{784,i}*x_{784,i}+b_{i} outputi=W1,i∗x1+W2,i∗x2+...+W783,i∗x783,i+W784,i∗x784,i+bi
y j ^ = e x p ( o u t p u t j ) ∑ i = 1 10 e x p ( o u t p u t i ) \hat{y_j}=\frac{exp(output_j)}{\sum_{i=1}^{10}{exp(output_i)}} yj^=∑i=110exp(outputi)exp(outputj)
最终损失函数为
L o s s = − 1 64 ∑ j = 1 64 l o g ( e x p ( o u t p u t j ) ∑ i = 1 10 e x p ( o u t p u t i ) ) Loss=-\frac{1}{64}\sum_{j=1}^{64}{log(\frac{exp(output_j)}{\sum_{i=1}^{10}{exp(output_i)}})} Loss=−641j=1∑64log(∑i=110exp(outputi)exp(outputj))
5.梯度下降优化参数
此时需要用梯度下降优化参数
W i = W i − η b a t c h s i z e ∑ i = 1 b a t c h s i z e d L o s s d w i b i = b i − η b a t c h s i z e ∑ i = 1 b a t c h s i z e d L o s s d b i W_i=W_i-\frac{\eta}{batchsize}\sum_{i=1}^{batchsize}{\frac{d_{Loss}}{dw_i}}\\ b_i=b_i-\frac{\eta}{batchsize}\sum_{i=1}^{batchsize}{\frac{d_{Loss}}{db_i}} Wi=Wi−batchsizeηi=1∑batchsizedwidLossbi=bi−batchsizeηi=1∑batchsizedbidLoss
其中 η \eta η为学习速率,batchsize是批量大小, d L o s s d w i \frac{d_{Loss}}{dw_i} dwidLoss为 w i w_i wi对损失函数的偏导
假设此时 y ^ \hat{y} y^的对应的类别是预测对的
即按照链式求导法则
KaTeX parse error: Got function '\hat' with no arguments as subscript at position 45: …ac{d_{Loss}}{d_\̲h̲a̲t̲{y}} \frac{d_\h…
因此,更新函数变成了
W i = W i − η b a t c h s i z e ∑ i = 1 b a t c h s i z e ( y ^ − 1 ) ∗ x i W_i=W_i-\frac{\eta}{batchsize}\sum_{i=1}^{batchsize}{(\hat{y}-1)*x_i} Wi=Wi−batchsizeηi=1∑batchsize(y^−1)∗xi
这里就是
W i = W i − η 64 ∑ i = 1 64 ( y ^ − 1 ) ∗ x i W_i=W_i-\frac{\eta}{64}\sum_{i=1}^{64}{(\hat{y}-1)*x_i} Wi=Wi−64ηi=1∑64(y^−1)∗xi
同理
b i = b i − η 64 ∑ i = 1 64 ( y ^ − 1 ) b_i=b_i-\frac{\eta}{64}\sum_{i=1}^{64}{(\hat{y}-1)} bi=bi−64ηi=1∑64(y^−1)
同理,假设此时 y ^ \hat{y} y^的对应的类别是预测错误的
d L o s s d w i = y ^ ∗ x i \frac{d_{Loss}}{dw_i}=\hat{y}*x_i dwidLoss=y^∗xi
W i = W i − η 64 ∑ i = 1 64 y ^ ∗ x i W_i=W_i-\frac{\eta}{64}\sum_{i=1}^{64}{\hat{y}*x_i} Wi=Wi−64ηi=1∑64y^∗xi
b i = b i − η 64 ∑ i = 1 64 y ^ b_i=b_i-\frac{\eta}{64}\sum_{i=1}^{64}{\hat{y}} bi=bi−64ηi=1∑64y^
(推算过程我就省略了,Latex打上去太累了)
PS:我吐了,上面这个求导我一开始没用链式求导,直接手算, o u t p u t i output_i outputi没经过softmax变换,直接当成了 y ^ \hat{y} y^来算,最后结果完全不符合逻辑,半夜看了好多博客终于想起来自己的问题了,好不容易重新推了出来
因此,最终W和b的优化函数如下:
W i = W i − η 64 ∑ i = 1 64 ( y ^ − y ) ∗ x i W_i=W_i-\frac{\eta}{64}\sum_{i=1}^{64}{(\hat{y}-y)*x_i} Wi=Wi−64ηi=1∑64(y^−y)∗xi
b i = b i − η 64 ∑ i = 1 64 ( y ^ − y ) b_i=b_i-\frac{\eta}{64}\sum_{i=1}^{64}{(\hat{y}-y)} bi=bi−64ηi=1∑64(y^−y)
最终代码如下:
w_,b_=CrossEntropyLoss(data,target,y_hat)
w=w+w_ #优化参数w的矩阵
b=b+b_ #优化参数b的矩阵
def CrossEntropyLoss(data,target,y_hat):
target = np.eye(10)[target] # 改为one-hot形式
data=data.T #(784,64)
#y_hat-target为预测值与实际值的one-hot挨个做差,得出一个(64,10)的y_hat-y的矩阵
w_=-np.dot(data,y_hat-target)/batch_size*learning_rate
b_=-(y_hat-target)/batch_size*learning_rate
# print(w_)
return w_,b_
这短短12行代码我查公式整理原理,搞了一个晚上。。。
最后优化时采用了矩阵相乘的方式代替累加
即 W i = W i − η 64 ∑ i = 1 64 ( y ^ − y ) ∗ x i W_i=W_i-\frac{\eta}{64}\sum_{i=1}^{64}{(\hat{y}-y)*x_i} Wi=Wi−64ηi=1∑64(y^−y)∗xi中的 ∑ i = 1 64 ( y ^ − y ) ∗ x i \sum_{i=1}^{64}{(\hat{y}-y)*x_i} i=1∑64(y^−y)∗xi
直接用矩阵相乘的方法代替

这里相乘时,为该矩阵的每行元素

与另一矩阵的每列的元素,挨个相加并且求和
如: x 1 , 1 ∗ ( y ^ 1 , 1 − y 1 , 1 ) + x 1 , 2 ( y ^ 1 , 2 − y 1 , 2 ) + . . . x 1 , 63 ( y ^ 1 , 63 − y 1 , 63 ) + x 1 , 64 ( y ^ 1 , 64 − y 1 , 64 ) x_{1,1}*(\hat{y}_{1,1}-y_{1,1})+x_{1,2}(\hat{y}_{1,2}-y_{1,2})+...x_{1,63}(\hat{y}_{1,63}-y_{1,63})+x_{1,64}(\hat{y}_{1,64}-y_{1,64}) x1,1∗(y^1,1−y1,1)+x1,2(y^1,2−y1,2)+...x1,63(y^1,63−y1,63)+x1,64(y^1,64−y1,64)
也就一一对应着 ∑ i = 1 64 ( y ^ − y ) ∗ x i \sum_{i=1}^{64}{(\hat{y}-y)*x_i} i=1∑64(y^−y)∗xi
计算准确率
def Accuracy(target,y_hat):
#y_hat.argmax(axis=1)==target 用于比较y_hat与target的每个元素,返回一个布尔数组
acc=y_hat.argmax(axis=1) == target
acc=acc+0 #将布尔数组转为0,1数组
return acc.mean() #通过求均值算出准确率
最终整个项目完整代码如下
from torchvision import datasets, transforms
import torch.utils.data as Data
import numpy as np
from tqdm._tqdm import trange
batch_size = 64
learning_rate=0.0001
def load_data():
# 加载torchvision包内内置的MNIST数据集 这里涉及到transform:将图片转化成torchtensor
train_dataset = datasets.MNIST(root='./data/', train=True, transform=transforms.ToTensor(), download=True)
test_dataset = datasets.MNIST(root='./data/', train=False, transform=transforms.ToTensor())
# 加载小批次数据,即将MNIST数据集中的data分成每组batch_size的小块,shuffle指定是否随机读取
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = Data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)
return train_loader,test_loader
def train(train_loader):
list=[]
w=np.random.normal(scale=0.01,size=(784,10)) #生成随机正太分布的w矩阵
b=np.zeros((batch_size,10)) #生成全是0的b矩阵
for i in trange(0,100):
for batch_idx, (data, target) in enumerate(train_loader):
if(data.shape[0]<batch_size):
break
data= np.squeeze(data.numpy()).reshape(batch_size,784) # 把张量中维度为1的维度去掉,并且改变维度为(64,784)
target = target.numpy() #x矩阵 (64,784)
y_hat=softmax(np.dot(data,w)+b)#预测结果y_hat
# print(sum(y_hat[0]))
w_=GradientOfCrossEntropyLoss(data,target,y_hat,type="weight")#计算交叉熵损失函数对于w的梯度
b_=GradientOfCrossEntropyLoss(data,target,y_hat,type="bias")#计算交叉熵损失函数对于b的梯度
w=GradientDescent(w,w_) #梯度下降优化参数w
b=GradientDescent(b,b_) #梯度下降优化参数b
list.append(Accuracy(target, y_hat))
if (batch_idx == 50):
print(Accuracy(target, y_hat))
return list
def softmax(label):
label = np.exp(label.T)#先把每个元素都进行exp运算
# print(label)
sum = label.sum(axis=0) #对于每一行进行求和操作
#print((label/sum).T.sum(axis=1))
return (label/sum).T #通过广播机制,使每行分别除以各种的和
#梯度下降
def GradientDescent(Param,GradientOfLoss):
Param = Param -GradientOfLoss/ batch_size * learning_rate
# print(w_)
return Param
#计算交叉熵损失函数对于w或者b的梯度
def GradientOfCrossEntropyLoss(data,y,y_hat,type="weight"):
y = np.eye(10)[y] # 改为one-hot形式
data=data.T #(784,64)
#y_hat-target为预测值与实际值的one-hot挨个做差,得出一个(64,10)的y_hat-y的矩阵
if (type == "bias"):
return y_hat-y
else:
return np.dot(data,y_hat-y)
def Accuracy(target,y_hat):
#y_hat.argmax(axis=1)==target 用于比较y_hat与target的每个元素,返回一个布尔数组
acc=y_hat.argmax(axis=1) == target
acc=acc+0 #将布尔数组转为0,1数组
return acc.mean() #通过求均值算出准确率
if __name__ == '__main__':
train_loader,test_loader=load_data() #加载数据(这里使用pytorch加载数据,后面用numpy手写)
list=train(train_loader)
import matplotlib.pyplot as plt
plt.plot(list)
plt.show()
