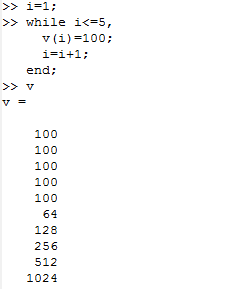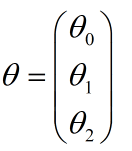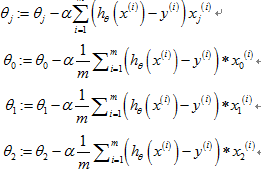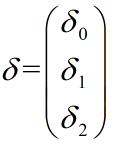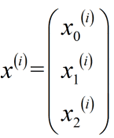吴恩达机器学习笔记（五）-Octave教程
第六章 Octave/Matlab教程
基本操作
一些想要构建大规模机器学习项目的人通常会使用Octave，这是一种很好的原始语言来构建算法原型。
本章节将介绍一系列的Octave命令：
（1）可以执行最基础的数学运算和逻辑运算。
（2）V=1:0.1:2，表示的是从1开始，每次步长为0.1，一直增加到2。
（3）V=1:6，这样v就被赋值了，从1到6。
（4）Ones(2,3)会得到两行三列的矩阵，并且值都为1，同理，zeros(1,3)会得到一行三列的矩阵，并且值都为0。
（5）Rand(1,3)会得到一行三列的矩阵，并且值从0~1中随机产生。
（6）Randn(1,3)同上，但是得到的值它们服从高斯分布。
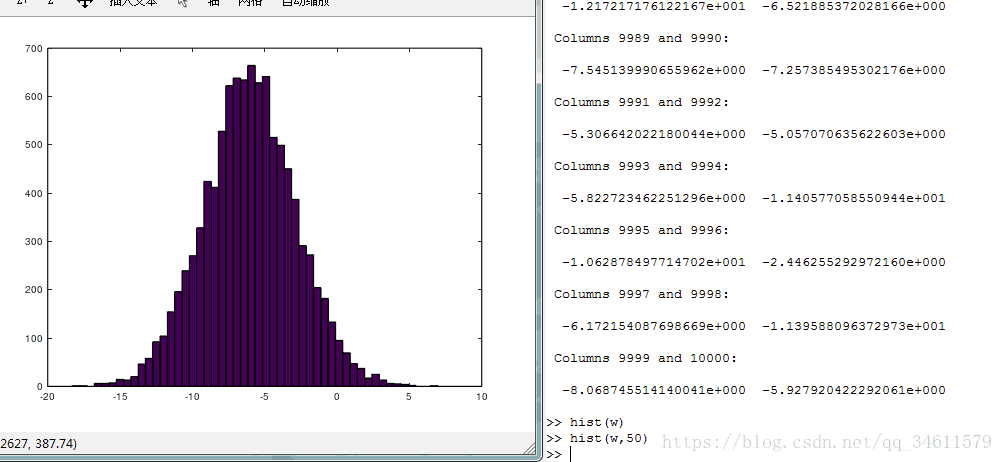
（7）使用hist命令可以绘制一个直方图，下面是生成的高斯分布直方图：
（8）生成矩阵的特殊命令：eye()表示生成单位矩阵。例如，eye(3)就可以生成一个3*3的单位矩阵：
（9）Help命令可以显示命令的帮助文档
（10）size()返回矩阵的大小；Length()返回向量的最大维数，如果是矩阵，返回较大的那个维数。
移动数据
如何在文件系统中查找和加载数据？
pwd显示的是Octave当前所在的路径。
cd表示改变路径；ls表示显示当前目录下的文件；
用load来加载文件数据；who能显示出当前Octave在内存中存储的所有变量；whos能显示更详细的变量信息；clear进行删除；save将数据存储进硬盘；
如何操作数据？
索引：A(3,2)表示的是第3行第2列的数值；A(2,:)表示A的第2行的所有元素（“：”表示该行或该列的所有元素）；A(:,2)表示A的第2列的所有元素;A([1 3],:)表示的是A中第一索引为1和3的所有元素，即1和3表示将从第1行和第3行取元素，冒号表示的是第一列和第二列的所有元素。
A(:)是一个很特别的语法，表示将A中的所有元素放入一个单独的列向量。
A和B是两个矩阵：
通过C=[A B]或者C=[A，B]将两个矩阵放在一起，矩阵A在左边，矩阵B在右边；
通过C=[A；B]将两个矩阵放在一起，矩阵A在上边，矩阵B在下边；
通过以上的命令可以实现快速组合复杂的矩阵和移动数据。
计算数据
如何对数据进行运算操作？
magic函数会返回名为幻方的矩阵。
幻方具有特殊的数学性质：它的任意行、列、对角线中的元素加起来都等于相同的值，虽然在机器学习算法中基本用不到这个概念，但是利用这个函数随机生成一个方阵还是很便捷的。
sum求和函数与prod求积函数；floor函数向下取整与ceil函数向上取整。
max(A,[],1)会得到A矩阵中每一列的最大值；
max(A,[],2) 会得到A矩阵中每一行的最大值；
max(A) 默认会得到A矩阵中每一列的最大值；
max(A(:))或max(max(A))可以得到A矩阵的最大值；
flipud(A)可以将A矩阵进行翻转；
pinv(A)可以求A矩阵的逆（伪逆）。
数据绘制
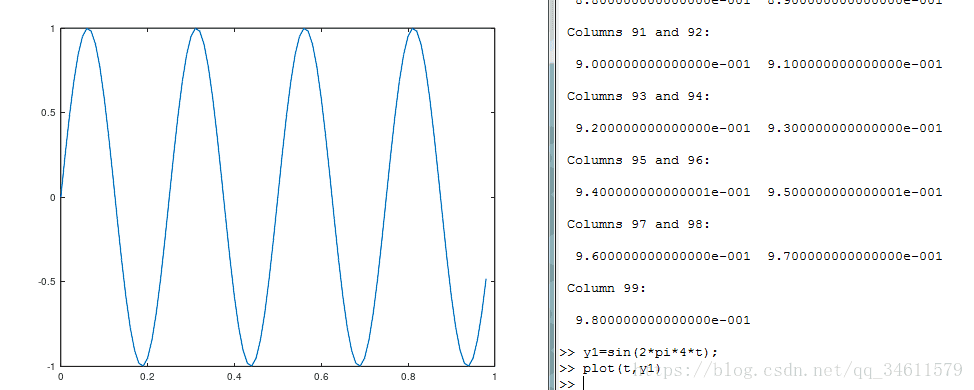
（1）利用plot函数，绘制y1=sin(2*pi*4*t)的图像，如图：
（2）利用plot函数，绘制y2=cos(2*pi*4*t)的图像，如图：
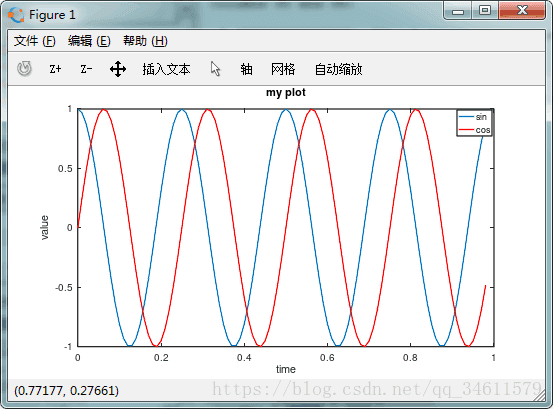
使用hold on函数可以让Octave在旧的图像上绘制新的图像，同时可以使用xlabel与ylabel给图像的x轴和y轴加上标签，使用legend(‘sin’,’cos’)可以给图像的右上角标记；使用title(‘my plot’)可以在图像的的顶部显示这幅图的标题。
可以使用print -dpng‘myplot.png’可以将图像保存为png格式文件。
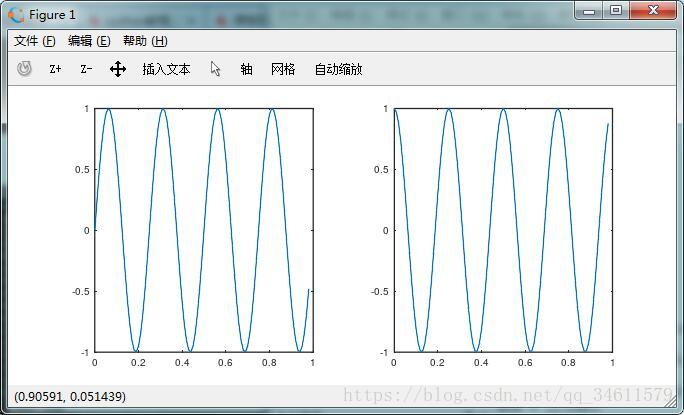
使用subplot(1,2,1)可以将图像分成1*2的格子，最后一个1表示使用第二个格子，同理subplot(1,2,2)中最后一个2表示使用第二个格子，如下图：
可以使用axis([0.5 1 -1 1])来改变x轴和y轴的范围，如图：
clf命令可以用于清除一幅图像；
使用imagesc(A)将绘制一个5*5的矩阵，它将矩阵画成一个5*5的彩色格图，其中不同的颜色对应A矩阵中的不同值，如图：
还可以使用imagesc(A), colorbar, colormap gray;同一时间运行三个命令生成了一个颜色图像—一个灰度分布图，并在右侧加入了一个颜色条，如图：
总结一下：本节中的图像绘制用了逗号连接的函数调用方式，这是Octave中的一种便捷的方式，将多条命令写在同一行中。控制语句for、while、if
如何使用好控制语句？
Octave里使用for循环：
Octave里使用while循环：
Octave里使用while循环和if条件语句：
Octave里使用if-else语句结构：
如何定义和使用函数？
将文件名就设置为函数名，可以利用addpath()将路径设置为Octave的搜索路径，这样即使不在文件的路径下，Octave也会在文件路经下寻找函数。
Octave和其他编程语言的语法结构都不同的一点是：它可以是一个函数返回多个值。
假设有这样的数据集，比如像下图这样：
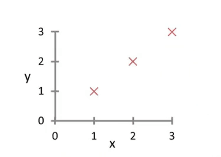
数据点为(1,1)，(2,2)，(3,3)，目标是定义一个Octave函数来计算代价函数J(θ)的，不同的θ值所对应的代价函数J。
定义函数如下：
对于数据集，设置为（1,2,3）y也为（1,2,3），假设θ0=0，θ1=1，给出的恰好是45度的斜线，可以完美拟合数据集，计算出的代价函数j=0；假设θ0=0，θ1=1，计算机出的代价函数j=2.3333，实际上就等于（1^2+2^2+3^2）/（2*3）。
总结：从上述的计算结果可以验证了这里定义的函数正确的计算出了正确的代价函数。
矢量
如何使Octave程序运行的更高效，可以运用内置的线性函数库。例如：与其自己写一个矩阵相乘的算法，不如直接在Octave里输入A*B就可以直接得到结果；如果使用了合适的向量化方法代码会简单很多、有效很多。
具体向量事例一：
将求和的过程用向量的乘积表示：
两种不同的思考方式，它们的求解过程也是不一样的
（1）没有进行向量化的过程：
（2）进行向量化的过程：
具体向量事例二：
用向量化的方法来实现上诉的更新规则：
把θ看作是一个向量，使θ：=θ-αδ，这里的
。
这里把θ看作一个n+1维的向量，α是一个实数，δ是一个n+1维的向量，所以这是一个向量减法运算。δ的第一个元素就是
，所以如果δ的下标从0开始，则：
δ0就等于
，δ的计算就是一个总和，由实数
乘以n+1维的向量
，向量
如下所示：
从上述给出的向量解释，就可以根据给出的
θ：=θ-αδ进行同步更新。