【算法学习笔记十二】回溯法(一)

回溯是一种有组织的详尽搜索，它通常避免搜索所有的可能性。它通常适用于需要检查大量但有限数量的解决方案的问题。

 3着色问题

3着色问题:给出一个无向图G=(V,E),需要用三种颜色之一为V中的每个顶点着色,三种颜色分别为1,2和3,使得没有两个邻接的顶点有同样的颜色。我们把这样的着色称为合法的;否则,如果两个邻接的顶点有同一种颜色就是非法的。一种着色可以用n元,组(c1, c2, .,cn)来表示,使ci∈{1,2,3}。例如, (1,2,2,3,1)表示一个有5个顶点的图的着色。一个n个顶点的图共有种可能的着色(合法的和非法的) ,所有可能的着色的集合可以用一棵完全的三叉树来表示,称为搜索树。在这棵树中,从根到叶节点的每一条路径代表一种着色指派。下图显示了有三个顶点的图的这样一棵树。

如果没有两个邻接的着色顶点有同样的颜色，图的一个不完全着色称为部分解。

回溯法通过每次一个节点地生成基底树来工作。如果从根到当前节点的路径对应于一个合法着色，过程就终止(除非期望找到不止一种的着色)。如果这条路径的长度小于n，并且相应的着色是部分的，那么就生成现节点的一个子节点,并将它标记为现节点。另一方面,如果对应的路径不是部分的，那么现节点标识为死节点并生成对应于另一种颜色的新节点。如果所有三种颜色都已经试过且没有成功，搜索就回溯到父节点,它的颜色被改变,依次类推。

    3-COLORREC
    Input:无向图G=(V,E)
    Output: G的顶点的3着色 c[1..n]其中每个c[j]为1, 2 或 3
        1. for k←1 to n
        2.     c[k]←0
        3. end for
        4. flag←false
        5. graphcolor(1)
        6. if flag then output c
        7. else output “no solution”

    Procedure graphcolor(k)
        1. for color=1 to 3
        2.     c[k]←color
        3.     if c 为合法着色 then set flag←true and exit
        4.     else if c 是部分的 then graphcolor(k+1)
        5. end for

最坏的时间复杂度为，是一个指数型时间算法。

N皇后问题

如何在nxn的国际象棋棋盘上安排n个皇后,使得没有两个皇后能互相攻击?如果两个皇后处在同一行、同一列或同一条对角线上,则她们能互相攻击。以4皇后为例，可推广到n皇后问题，最坏时间复杂度为。

    4-QUEENS
    Input: 空
    Output:对应于4皇后问题的解的向量 x[1..4] 
        1. for k←1 to 4
        2.     x[k]←0      {没有皇后放置在棋盘上}
        3. end for
        4. flag←false
        5. k←1
        6. while k≥1
        7.     while x[k]≤3
        8.         x[k]←x[k]+1
        9.         if x 为合法着色 then set flag←true and 且从两个while循环推出
      10.          else if x i是部分解 then k←k+1      {前进}
      11.     end while
      12.     x[k]←0
      13.     k←k-1      {回溯}
      14. end while
      15. if flag then output x
      16. else output “no solution”

4皇后回溯过程

 

一般回溯方法

在回溯法中，解向量中每个xi都属于一个有限的线序集Xi，因此，回溯算法按词典序考虑笛卡儿积中的元素。算法最初从空向量开始，然后选择X1中最小的元素作为x1，如果(x1)是一个部分解，算法通过从X2中选择最小的元素作为x2继续，如果(x1,x2)是一个部分解，那么就包括X3中最小的元素，否则x2被置为X2中的下一个元素。一般地，假定算法已经检测到部分解为(x1, x2, ..,xj )，它然后再去考虑向量v=(x1,, ...xj,x(j+1))，我们有下面的情况。

(1)如果v表示问题的最后解，算法记录下它作为一个解，在仅希望获得一个解时终止,或者继续去找出其他解。

(2) (向前步骤)。如果v表示一个部分解，算法通过选择集合X(j+2)中的最小元素向前。

(3)如果v既不是最终的解，也不是部分解,则有两种子情况。

    (a)如果从集合X(j+1)中还有其他的元素可选择，算法将x(j+1)置为X(j+1)中的下一个元素。

    (b) (回溯步骤)。如果从集合X(j+1)中没有更多的元素可选择，算法通过将 xj置为Xj中的下一个元素回溯；如果从集合Xj中仍然没有其他的元素可以选择,算法通过将xj(j-1)置为X(j-1)中的下一个元素回溯,依次类推。

    BACKTRACKREC(递归)
    Input:集合 X1,...,Xn的清楚的或者隐含的描述
    Output:解向量v=(x1,...xi), 0≤i≤n
        1. v←()
        2. flag←false
        3. advance(1)
        4. if flag then output v
        5. else output “no solution”
    
    Procedure advance(k)
        1. for each x∈Xk
        2.     xk←x; append xk to v
        3.     if v 为最终解 then set flag←true and exit
        4.     else if v 是部分解 then advance(k+1)
        5. end for

    BACKTRACKITER(迭代)
    Input: Explicit or implicit description of the sets X1,...,Xn
    Output: A solution vector v=(x1,...xi), 0≤i≤n
        1. v←()
        2. flag←false
        3. k←1
        4. while k≥1
        5.     while Xk 没有被穷举
        6.         xk←Xk中的下一个元素; append xk to v
        7.         if v 为最终解 then set flag←true and exit from the two while loops
        8.         else if v is partial then k←k+1      {前进}
        9.     end while
      10.     重置Xk 使得下一个元素排在第一位
      11.     k←k-1      {回溯}
      12. end while
      13. if flag then output v
      14. else output “no solution”

分支限界法

分支限界法 是一种有组织的穷举算法，主要用于求解最优化问题

解空间树的动态搜索

首先确定一个合理的限界函数，并根据限界函数确定目标函数的界[down, up] 。

按照广度优先策略遍历问题的解空间树，在分支结点上，依次搜索该结点的所有子结点，分别估算这些子结点的目标函数的可能取值，如果某子结点的目标函数可能取得的值超出目标函数的界，则将其丢弃，因为从这个结点生成的解不会比目前已经得到的解更好；否则，将其加入待处理结点表（表PT）中。

依次从表PT中选取使目标函数的值取得极值的结点成为当前扩展结点，重复上述过程，直到找到最优解。

随着这个遍历过程的不断深入，表PT中所估算的目标函数的界越来越接近问题的最优解。

当搜索到一个叶子结点时：

–i) 如果该结点的目标函数值是表PT中的极值（对于最小化问题，是极小值；对于最大化问题，是极大值），则该叶子结点对应的解就是问题的最优解；

–ii) 否则，根据这个叶子结点调整目标函数的界（对于最小化问题，调整上界；对于最大化问题，调整下界），依次考察表PT中的结点，将超出目标函数界的结点丢弃，然后从表PT中选取使目标函数取得极值的结点继续进行扩展。

0/1背包问题：

假设有4个物品，其重量分别为(4, 7, 5, 3)，价值分别为(40, 42, 25, 12)，背包容量W=10。首先，将给定物品按单位重量价值从大到小排序，结果如下：

物品	重量(w)	价值(v)	价值/重量(v/w)
1	4	40	10
2	7	42	6
3	5	25	5
4	3	12	4

求得近似解为(1, 0, 0, 0)，获得的价值为40，这可以作为0/1背包问题的下界。

考虑最好情况，背包中装入的全部是第1个物品且可以将背包装满，则可以得到一个非常简单的上界的计算方法：ub=W×(v1/w1)=10×10=100。

目标函数的界：[40, 100]。

限界函数为: (v表示已放入背包的物品，i表示前i个物品处理完) 

搜索过程：

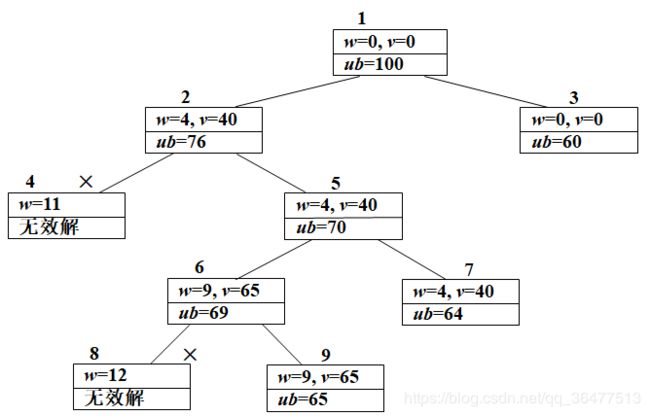
（1）在根结点1，没有将任何物品装入背包，因此，背包的重量和获得的价值均为0，根据限界函数计算结点1的目标函数值为10×10=100；

（2）在结点2，将物品1装入背包，因此，背包的重量为4，获得的价值为40，目标函数值为40 + (10-4)×6=76，将结点2加入待处理结点表PT中；在结点3，没有将物品1装入背包，因此，背包的重量和获得的价值仍为0，目标函数值为10×6＝60，将结点3加入表PT中；

（3）在表PT中选取目标函数值取得极大的结点2优先进行搜索；

（4）在结点4，将物品2装入背包，因此，背包的重量为11，不满足约束条件，将结点4丢弃；在结点5，没有将物品2装入背包，因此，背包的重量和获得的价值与结点2相同，目标函数值为40 + (10-4)×5=70，将结点5加入表PT中；

（5）在表PT中选取目标函数值取得极大的结点5优先进行搜索；

（6）在结点6，将物品3装入背包，因此，背包的重量为9，获得的价值为65，目标函数值为65 + (10-9)×4=69，将结点6加入表PT中；在结点7，没有将物品3装入背包，因此，背包的重量和获得的价值与结点5相同，目标函数值为40 + (10-4)×4＝64，将结点6加入表PT中；

（7）在表PT中选取目标函数值取得极大的结点6优先进行搜索；

（8）在结点8，将物品4装入背包，因此，背包的重量为12，不满足约束条件，将结点8丢弃；在结点9，没有将物品4装入背包，因此，背包的重量和获得的价值与结点6相同，目标函数值为65；

（9）由于结点9是叶子结点，同时结点9的目标函数值是表PT中的极大值，所以，结点9对应的解即是问题的最优解，搜索结束。

分支界限法的设计思想

假设求解最大化问题，解向量为X=(x1, x2, …, xn)，其中，xi的取值范围为某个有穷集合Si，|Si|=ri（1≤i≤n）。

在使用分支限界法搜索问题的解空间树时，首先根据限界函数估算目标函数的界[down, up]，然后从根结点出发，扩展根结点的r1个子结点，从而构成分量x1的r1种可能的取值方式。对这r1个子结点分别估算可能取得的目标函数值bound(x1)，其含义是以该子结点为根的子树所可能取得的目标函数值不大于bound(x1)，也就是部分解应满足：

bound(x1)≥bound(x1, x2)≥ … ≥bound(x1, x2, …, xk)≥ … ≥bound(x1, x2, …, xn)

若某子结点的目标函数值超出目标函数的界，则将该子结点丢弃；否则，将该子结点保存在待处理结点表PT中。从表PT中选取使目标函数取得极大值的结点作为下一次扩展的根结点，重复上述过程，当到达一个叶子结点时，就得到了一个可行解X=(x1, x2, …, xn)及其目标函数值bound(x1, x2, …, xn)。

如果bound(x1, x2, …, xn)是表PT中目标函数值最大的结点，则bound(x1, x2, …, xn)就是所求问题的最大值，(x1, x2, …, xn)就是问题的最优解；

如果bound(x1, x2, …, xn)不是表PT中目标函数值最大的结点，说明还存在某个部分解对应的结点，其上界大于bound(x1, x2, …, xn)。于是，用bound(x1, x2, …, xn)调整目标函数的下界，即令down=bound(x1, x2, …, xn)，并将表PT中超出目标函数下界down的结点删除，然后选取目标函数值取得极大值的结点作为下一次扩展的根结点，继续搜索，直到某个叶子结点的目标函数值在表PT中最大。

分支限界法求解最大化问题的一般过程：

1．根据限界函数确定目标函数的界[down, up]；

2．将待处理结点表PT初始化为空；

3．对根结点的每个子结点x执行下列操作

      3.1 估算结点x的目标函数值value;

      3.2 若(value>=down)，则将结点x加入表PT中；

4．循环直到某个叶子结点的目标函数值在表PT中最大

      4.1  i=表PT中值最大的结点；

      4.2 对结点i的每个子结点x执行下列操作

           4.2.1 估算结点x的目标函数值value;

           4.2.2 若(value>=down)，则将结点x加入表PT中；

           4.2.3 若(结点x是叶子结点且结点x的value值在表PT中最大)，

                    则将结点x对应的解输出，算法结束；

           4.2.4 若(结点x是叶子结点但结点x的value值在表PT中不是最大)，

                    则令down=value，并且将表PT中所有小于value的结点删除；

回溯法(二)