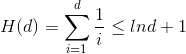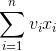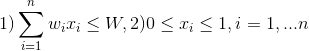【算法学习笔记十四】近似算法

有许多困难的组合优化问题，使用回溯或随机化不能有效地解决。

组合优化问题:在有限的可能性中找出最优解。一个近似算法将给出一个合理的解，逼近一个最优解。(大多数)近似算法的标记特征是它们是快速的(多项式时间算法)。然而，人们不应该乐观地寻找一个有效的近似算法，因为有一些困难的问题，即使存在一个合理的近似算法是不可能的，除非NP=P。

组合优化问题

输入:COP的实例I。

可行集:FEAS(1) =实例I的所有可行(或有效)解的集合，通常用一组约束表示。

目标成本函数:实例I包括对目标成本函数的描述。Cost[l]映射每个解决方案S(可行或不可行)一个实数或±。

目标:优化(即最小化或最大化)目标成本函数。

优化设置:OPT(I) ={Sol ∈ FEAS(I) | Cost[I] (Sol) ≤ Cost[i] (Sol')， VSol' ∈FEAS(1)}，成本最小值的集合≤实例I可行的解决方案；

组合:指问题结构意味着只有有限数量的解决方案需要被检查以找到最优。

输出:一个解决方案Sol ∈ OPT(I)，或报告FEAS(I) = 。

COP举例：

“Easy”(多项式时间可解)：最短(简单)路径，最小生成树，图匹配；

“NP-Hard”(没有已知的多项式时间解决方案):最长(简单)路径，旅行推销员，顶点覆盖，集合覆盖，K-Cluster，0/1 背包。

 

 分类

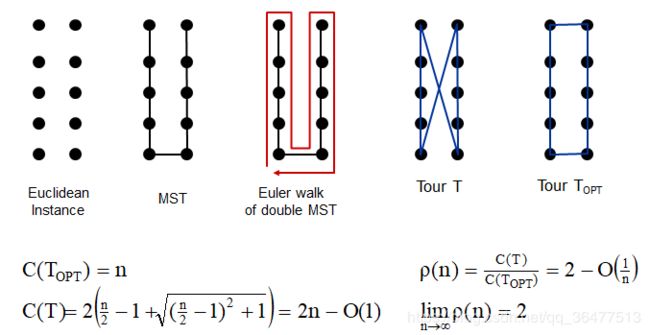
差界算法：

我们从近似算法中所能期望的最大结果是，最优解的值与通过近似算法得到的解的值之间的差总是不变的。对于所有问题的实例，可以得到一个近似算法A这样, K是常数。但是有差分界近似算法的NP-hard优化问题很少。

平面着色问题可以用近似算法求解；

背包问题不存在差界近似算法，除非NP=P；

装箱问题：给定一个集合，的大小是，其中每个s在0和1之间，我们需要将这些物品打包到单位容量的最小箱数。四种启发式方法:FF(最先适配，放第j个物品时，放入第一个可以放的箱子，且), BF(最优适配，放第j个物品时，使放入后箱子空余尽量少), FFD(先做从大到小的排序，在进行FF), BFD。

定理:对于装箱问题的所有实例I，

定理:对于装箱问题的所有实例I，

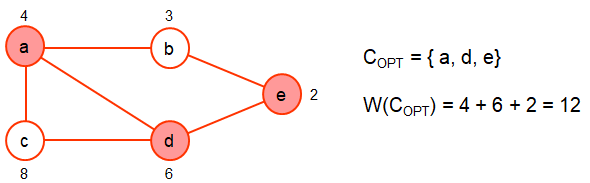
加权顶点覆盖问题：

输入:顶点权值为w(V)的无向图G(V,E)，w(v)>0是顶点vV的权值

输出:  顶点覆盖C:  CV覆盖所有的边

目标:最小化顶点覆盖C的权重

顶点覆盖问题表示为整数线性规划：，，约束条件为(P1)

求解：松弛——将整数线性规划变为线性规划问题，即(P2)

           对偶——(P3)

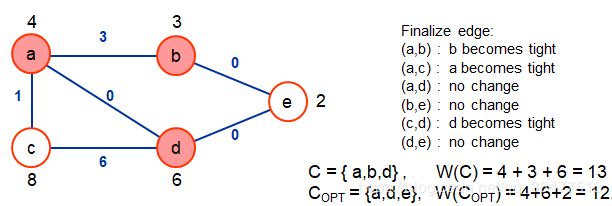
 当时，点v为tight；当u或者v是tight时，边(u,v)是final。

ALGORITHM Approximate-Vertex-Cover (G(V,E), w(V))
    for each edge (u,v)∈E  do   p(u,v) ← 0
    for each edge (u,v)∈E  do   finalize (u,v), i.e.,increase p(u,v) until u or v becomes tight,(取u，v中最小的，未取的减去最小的，更新price,0值放入到C中)
    C  ←  { v ∈ V |  v is tight }
    return C
end

 这是一个2-近似算法，有以下的特点：1）正确性，得到的C是可行解；2）多项式时间算法；3）

 

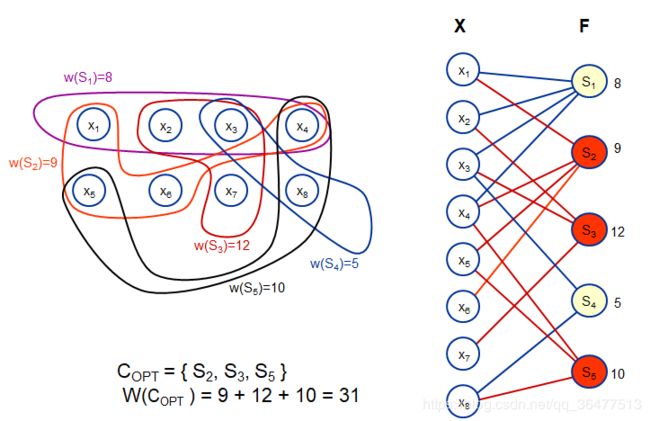
加权集合覆盖问题：，F包含m个X的子集，挑选C，使得C可以覆盖X，并使得权值尽可能地小：

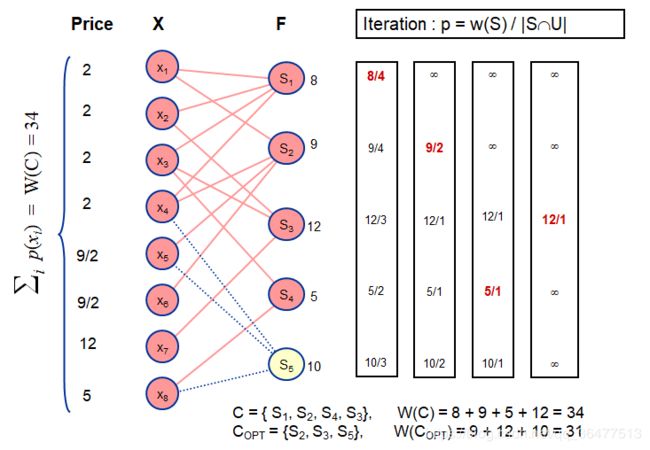
ALGORITHM   Greedy-Set-Cover (X, F, w(F))
1.     U ← X	(* uncovered elements *)
2.     C ← Ø	(* set cover *)
 while  U ≠ Ø  do 
      select S∈F that minimizes  price p = w(S) / |S∩U|
      U  ←  U - S
      C  ←  C ∪ {S} 
  return C
end

 

这是一个H(n)-近似算法(与n有关的)。

Harmonic Number：；

Maximumdegree：；

引理：；

定理：Greedy-Set-Cover算法的特点：正确性：输出可行解C；多项式运行时间；近似界：

旅行商问题(TSP)：

设nxn的矩阵，表示城市i到城市j的距离。输出路径T，T从起点出发，路过每个城市且仅路过一次，最后回到起点，找出一条最短的路径T。

最小生成树，哈密尔顿回路(HCP)，图的匹配，欧拉图都是NP-hard问题。

哈密尔顿回路：存在圈经过每一座城市且仅经过一次。

 定理：设是一个常数，一般的TSP问题的近似算法是NP-hard问题。(即不存在多项式时间近似算法)

metric-TSP：是一般TSP问题的特殊情况，也是NP-hard问题，存在2-近似算法，1.5-近似算法。欧拉图：对图G进行遍历，经过每条边且仅经过一次。

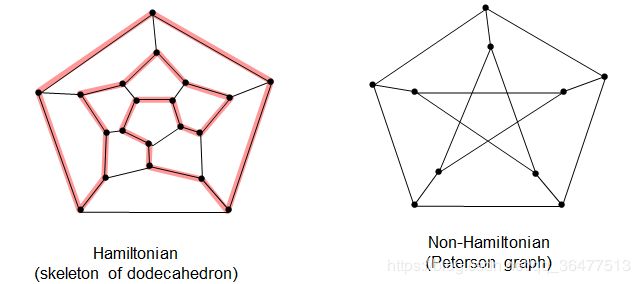
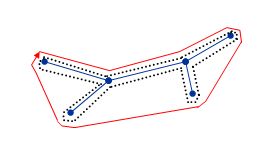
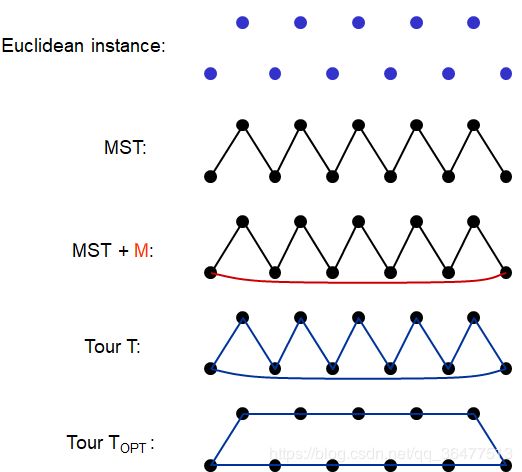
metric-TSP的2-近似算法：步骤，首先构造最小生成树，双边的MST的欧拉图了，跳过重复的点。

根据三角不等式，跳过重复点的操作不会增加哈密尔顿回路的长度 ，即哈密尔顿回路的长度不会超过欧拉图的长度。

2是“紧的”，是可达的

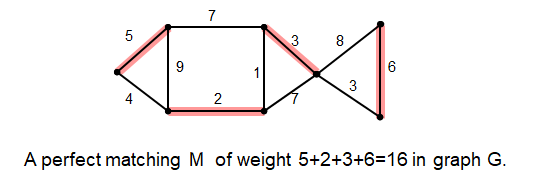
 metric-TSP的1.5-近似算法—图的匹配，匹配集M是G的一个子集，且满足任意两条边都没有公共的顶点。完美匹配，每个点都被匹配，即位于M中(偶数个点才存在完美匹配)。

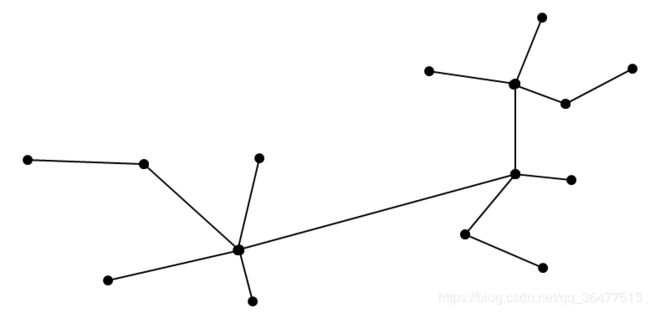
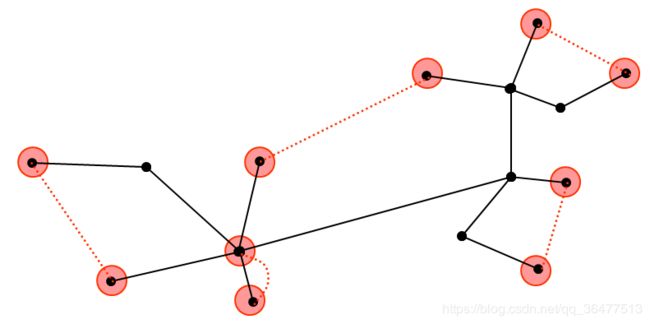
 步骤：构造MST

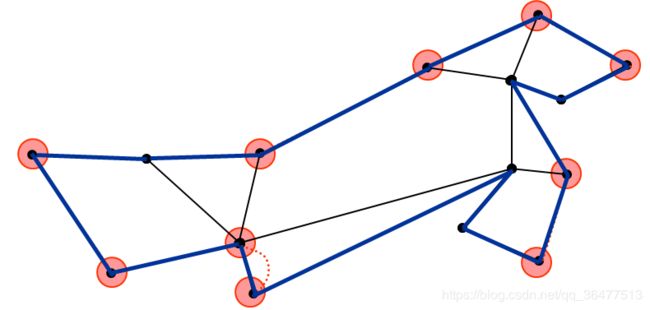
           找出其中度数为奇数的顶点，对找出的顶点找到最小权值的完美匹配M，E=MST+M，E是一个欧拉图

             跳过重复点的欧拉图得到TSP回路T。

 

1.5是可达的。

 K-聚类问题(The K-Cluster Problem)

设点集X，是之间的距离，以及正整数K，把X分成K类，并使得K类中最长的直径最小化，即。

n=17，K=4

 贪心算法;是2-近似多项式算法；

                 (1)贪婪地逐步的从X中取K个点作为集群的“中心”，并选择离之前选择的中心最远的集群中心。

                 (2)将剩余的X点分配给离中心最近的集群。

定义:是离最远的点。如果我们想要k+ 1个中心，，令r*=r(k+1)=min(d(x*，) ，j=1.k}。

引理:算法具有以下性质:(a)每个点距离其簇中心最多r*的距离。(b) K+1个点之间的距离至少为r*。

0/1背包问题(可切割Fractional)

最大化：

约束条件：

FKP的最优解可以在O(nlogn)时间内得到。

证明:

       贪心策略:按vi/wi的递减顺序考虑；

       将物品按顺序放在背包里，直到袋子装满；

       只有放在背包中的最后一件物品可能被分割；

       第一步的排序时间是O(nlogn)。

01KP approximation Greedy Algorithm
Input: 2n+1 positive integers corresponding to item weights {w1...wn}, item values {v1...vn} and the knapsack capacity W
Output: A subset Z of the items whose total size is at most W
    1. Renumber the items so that v1/w1...vn/wn
    2. j←0, K←0, V←0, Z←{}
    3. while j2
近似解是u1，最优解是u2，R=W/2，W可以任意取

  11. Let Z’={us}, where us is an item of maximizing value
  12. if Vvs then return Z
  13. else return Z’
加上后面的代码，此时近似度R=2

设,对于某个正整数k，算法，由两步组成。首先，选择最多有k个元素的子集，并在背包中取出它们。然后对剩余的项运行knapsack贪婪算法。这两个步骤重复，j是每个子集的大小，0≤j≤k。

定理15.4(PTAS):令对于k≥1，算法的运行时间为，性能比为。

 

 

近似算法：多项式运行时间；

PTAS(多项式时间近似策略)：额外输入参数e，作为相对误差的界；找到的相对误差最多为e；对于固定的e而言，关于输入规模的多项式运行时间

FPTAS：是一个PTAS，并关于输入规模和1/e的多项式时间。