遗传算法（四）MATLAB GA工具箱使用 附解TSP问题

• 笔记（一） 基本遗传算法
• 笔记（二） 遗传算法的优化改进
• 笔记（三） 遗传算法解组合优化
• 笔记（四） MATLAB遗传算法工具箱使用

基本使用

1. 直接参见函数ga

函数原型：[x fval] = ga(@fitnessfun, nvars, options)

x是使fitnessfun函数取最小值使的自变量值。nvars为自变量的数目即x向量中包含的元素个数，option可暂时不填。

[x, f] = ga(@cos, 1);

即得到一段简单的遗传算法代码，其作用为求解某函数的最小值。

如何调参：

x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,IntCon,options)

• A, b，Aep, beq, LB, UB为线性约束项，即满足如下约束：

Ax≤bAeq≤x≤beqLB≤x≤UB

• nonlcon为非线性约束nonlenear constraints。其中运用了矢量化约束（Vectorized Constraints）的方法。nonlcon是一个返回两个参数的函数句柄，可以是当前路径下的一个函数文件@functionfile。其具有如下原型：

    [c ceq] = nonlcon(x)

其约束为c≤0, ceq=0。举个例子（来自MATLAB help，直接截图）：
具有三个变量的规划中，有非线性约束：

则其向量化约束函数nonlcon可以写为：

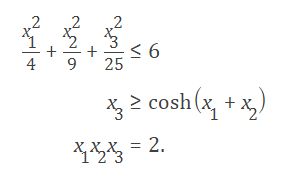
• IntCon：自变量向量正整数的下标，从1到nvars.

• options: 比较复杂，感兴趣的读者可以去查一下帮助文档。在这里举例用几个比较常用的option：

选项	功能	值
CrossoverFraction	交叉的概率	0-1的小数
EliteCount	用于精英原则， 每次遗传中一定会活下来的个体的个数	正整数
FitnessLimit	适应度的范围	标量/ {-Inf}
Generations	迭代遗传的次数	正整数
InitialPopulation	初始种群	可以用上一次遗传生成的种群 作为下一次GA的初始种群

option中的功能要通过gaoptimset('param1',value1,'param2',value2,...)的形式调用。

再调用一个简单的GA代码作结：

[x, f] = ga(@cos, 1, [], [], [], [], 0, 2 * pi, [], gaoptimset('CrossoverFraction', 0.3))

---

示例，解组合优化

1. 解TSP

由于MATLAB提供了很好的遗传算法接口，故对于用户来说只需要将问题抽象化，再进行编码、解码、计算适应度即可。

问题例子可以参考上一篇文章： 遗传算法（三）解TSP问题

这里直接给出适应度计算函数，包含编码和解码：

function Fitness = GA_TSPfun(chrom)
%% Create City
NumCity = 9;
Fitness = 0;
Dist =[0 2.8946 6.5107 5.5845 5.2429 5.8733 4.4377 2.7627 6.5644;
 2.8946 0 4.3313 5.1381 5.7211 3.1830 2.3729 5.2763 5.0574;
 6.5107 4.3313 0 3.6548 5.2943 1.8590 2.0889 9.2412 8.3103;
 5.5845 5.1381 3.6548 0 1.7362 4.8792 3.3486 8.190210.1465;
 5.2429 5.7211 5.2943 1.7362 0 6.2723 4.5224 7.531710.7633;
 5.8733 3.1830 1.8590 4.8792 6.2723 0 1.8705 8.4338 6.4969;
 4.4377 2.3729 2.0889 3.3486 4.5224 1.8705 0 7.1555 6.9906;
 2.7627 5.2763 9.2412 8.1902 7.5317 8.4338 7.1555 0 7.1508;
 6.5644 5.0574 8.310310.146510.7633 6.4969 6.9906 7.15080];

%% Decode:
order = [];
city = 1 : NumCity;
for j = 1 : NumCity 
    order = [order, city(1+rem( chrom(j)-1, length(city)))];
    city(1 + rem(chrom(j)-1, length(city))) = [];
end
for i = 1 : NumCity
    city1 = order(i);
    city2 = order(1 + rem(i, NumCity));
    Fitness = Fitness + Dist((city1-1)*NumCity + city2);
end
end

经验证发现，同样的TSP问题，MATLAB的GAtools得出的解大多为31.7, 33左右，逼近最优解。但是前一篇中作者自己编写的遗传算法程序，得出的平均结果为40左右。可见自己写的代码爬山能力还不够强，挖个坑，以后再研究一下。