Udacity机器人软件工程师课程笔记（三十四) - 占用栅格地图构建算法

一、 SLAM Algorithms 介绍

• Extended Kalman Filter SLAM(EKF) 扩展卡尔曼滤波SLAM
• Sparse Extended information Filter(SEIF) 稀疏扩展信息滤波
• Extended Information Form(EIF) 扩展信息滤波
• FastSLAM
• GraphSLAM

定位：

• 假设：已知地图
• 估计：机器人的轨迹

映射：

• 假设：机器人的轨迹
• 估算：地图

二、 映射/地图绘制

移动机器人的地图绘制是一个具有挑战性的问题，主要有两个原因。

第一，地图和姿态对机器人来说都是未知的，但这可以用占用栅格地图构建算法来解决。

第二， 巨大的假设空间，假设空间是在映射过程中形成的所有可能映射的空间。这个空间是高维的，因为地图是在一个连续的空间上定义的。尤其是当机器人被部署到一个开放的环境中，它们必须感知无限多的物体。

占用栅格地图构建算法给出了地图的离散近似，但是即使在这种离散近似下，所有可能映射的空间仍然会很大。所以现在的挑战是估算出完整的具有高维空间的后验地图。

我们在定位中用来估计后验姿态的基本滤波方法将有所不同，并且在映射中应使用对其的扩展以适应庞大的假设空间。

接下来是绘图的难点，

第一个困难是，环境的规模。由于要处理大量数据，因此很难绘制大区域的地图。

机器人板上的微控制器必须收集所有瞬时姿势和障碍物，然后形成结果图并相​​对于该图定位机器人。而且，当地图的尺寸​​大于机器人的感知范围时，映射问题将变得更加困难。但这只是问题的一部分。

感知传感器中始终存在噪声，测听传感器和执行器。在映射过程中，我们必须始终过滤掉来自这些传感器和执行器的噪声。对于大噪声，随着这种噪声加起来，映射变得更加困难且更具挑战性。

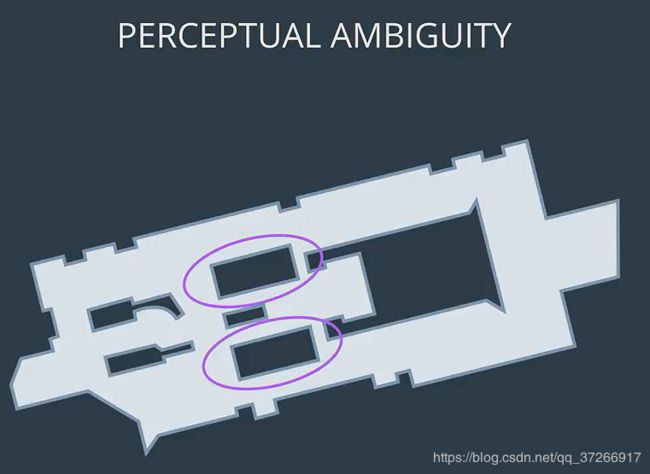
感知上的歧义是映射的另一个困难。当两个地方看起来相似时就会产生歧义，并且机器人必须在机器人在不同时间点经过的两个位置之间建立关联。当机器人以循环方式行驶时（例如，在走廊中来回走动），会出现另一个映射困难。循环行驶时，机器人测听仪会逐渐累积误差。在循环周期结束时，误差将会很大。

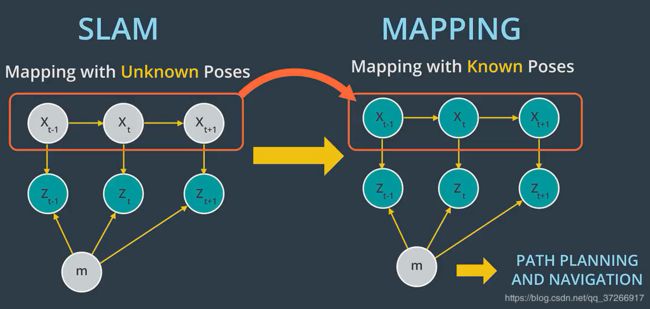
三、映射已知姿态

在假定机器人姿势已知且无噪声的假设下生成地图的问题称为具有已知姿势的映射。

该图中表示了已知的姿势问题，其中x代表姿势，z代表测量值，m代表地图。

占用栅格地图构建算法可以估计后验地图，从而给出嘈杂的测量结果和已知的姿势。在大多数机器人应用中，测距数据比较杂乱，我们不知道机器人的姿势，那为什么在这种情况下必须进行映射？

映射通常发生在SLAM之后，因此，映射的力量在于其后处理。在SLAM期间，问题从具有已知姿态变为具有未知姿态。

在SLAM期间，内置环境地图的机器人会相对于它定位。在SLAM之后，占用栅格映射算法使用从SLAM过滤的确切机器人姿态。然后，根据SLAM和噪声测量的已知姿态，映射算法将生成适合路径规划和导航的地图。

四、后验概率

后验概率

回到具有已知姿势的图形化图形模型，我们的目标是实现一个映射算法，并在有噪声测量和假定已知姿势的情况下估计地图。

已知姿势映射问题可以用$P(m|z_{1:t},x_{1:t})$函数表示。借助此功能，我们可以在给定时间t之前的所有测量值和时间t之前由机器人轨迹表示的所有姿势的情况下，在地图上计算后验。

在估算地图时，由于机器人路径是从SLAM提供给我们的，因此我们排除$u$的影响。但以后将在SLAM中包含，以估计机器人的轨迹。

2D地图

目前，我们将仅估算二维地图的后验。在现实世界中，通常将具有二维激光测距仪传感器的移动机器人部署在平面上，以捕获3D世界的一部分。这些二维切片将在每个瞬间合并并划分为网格单元，以通过占用栅格地图构建算法估计后验。三维地图也可以通过占用栅格地图构建算法进行估算，但是由于需要过滤掉大量的嘈杂的三维测量结果，因此需要更高的计算内存。

五、网格单元

为了估计后部地图，占用栅格将在有限数量的栅格单元中均匀地划分二维空间。这些栅格单元中的每个栅格单元将保留与其覆盖的位置相对应的随机值。根据测量数据，该栅格空间将填充零和一。如果激光测距仪传感器检测到障碍物，则该单元格将被视为已占用并且其值为1。对于自由空间，该单元格将被视为未占用，其值将为0。

现在，要找出可以从栅格单元中生成的地图的数量，让我们选择前两个单元并计算出它们的组合。

第一个组合（0，0）是具有两个自由空间的地图。第二个组合（0，1）是一张地图，左侧有一个自由空间，右侧有一个障碍物。通过翻转第二张地图，得到第三张组合（1，0）。第四组合(1， 1)是具有两个障碍的地图。因此，可以从这两个栅格单元中形成的地图总数等于四个。

概括起来，可以从栅格单元中形成的地图数量等于单元数量乘幂的两倍。

现在，想象一下拥有一个带有成千上万个栅格单元的2D空间， 生成的地图数量将更大。

六、后验概率的计算

方法一：$P(m\mid z_{1:t},x_{1:t})$
我们刚刚看到，地图具有高维性，所以在计算内存方面，用第一种方法计算后验太占用内存了。

方法二：$P(m_i|z_{1:t},x_{1:t})$
第二种或更好的估计后验图的方法是将这个问题分解成许多单独的问题。在每一个这样的问题中，我们都会在每个时刻计算后验地图$m_i$。

然而，这种方法仍然存在一些缺陷，因为我们正在独立地计算每个单元的概率。因此，我们仍然需要找到一种不同的方法来处理相邻单元之间的依赖关系。

方法三：${\prod }_{i}P(m_i|z_{1:t},x_{1:t})$
第三种方法是通过关联单元并克服庞大的计算内存来计算后部图的最佳方法， 就是用边际或因式分解的乘积来估计后验图。

七、滤波

1. 正向与反向测量模型

由于分解，我们现在需要解决一个二进制估计问题，其中栅格单元保持静态状态，该状态不会随时间变化。静态的意思是系统的状态在感测期间不会改变。

$$\prod _{i}p(m_i|z_{1:t},x_{1:t})$$

在本地，存在针对此问题的过滤器，称为二值贝叶斯过滤器。二进制贝叶斯滤波器通过采用信念的对数比值比来解决静态问题。在静态下，置信度现在仅是测量的函数。

根据所反映的测量值，更新栅格单元的状态，并且通过表示栅格单元相对于测量值的二进制状态的逆测量模型可以知道此信念。

当测量比二进制静态更复杂时，通常使用逆测量模型。

让我们以配备RGB-D相机的移动机器人为例。机器人的任务是估计此门是打开还是关闭。与门打开或关闭的简单二进制状态相比，由摄像机图像表示的测量范围巨大。

在这种情况下，使用反向传感器模型总是比使用正向传感器模型容易。二进制贝叶斯滤波器将使用对数优势比表示来求解逆测量模型。

为了表示$l_t$的对数比值比的置信度，二进制贝叶斯过滤器将置信度除以其取反，然后采用该表达式的对数形式。

使用对数优势比表示的优势是避免概率不稳定性接近零或一。

正向测量模型$-P(z_{1:t}|x)$:根据给定的系统状态估计后验值。
反向测量模型$-P(x|z_{1:t})$:估计一个后验超过系统状态给定的测量。

反向测量模型通常用于测量比系统状态更复杂的情况。

用对数比值表示的优点是避免了在0或1附近的概率不稳定性。另一个优点是系统的速度、准确性和简单性。可以查看这两个来源，以获得更多关于对数概率和数值稳定性的信息:

1. Log Probability
2. Numerical Stability

2. 静态二值贝叶斯滤波

我发现这里课程说的不清楚，所以引用了《概率机器人》中的解释和推导。

机器人技术中的某些问题表达为不随时间变化的二值状态的最优估计间题。
这些问题通过二值贝叶斯滤波(binary Bayes filter) 来阐述。如果一个机器人从传感器测量的序列中估计环境的一个固定的二值数，此时这类问题就产生了。例如，一个机器人可能想知道门是开着的还是关着的，并认为在检测期间门的状态不改变。

当状态静止时，置信度就仅是测量的函数：

$$be{l}_i(x)=p(x|z_{1:t},u_{1:t})=p(x|z_{1:t})$$

这里状态有两个可能值，用$x$ 和$x^{\prime }$ 表示。具体来说，有$be{l}_i(x^{\prime })=1-be{l}_t(x)$。状态x 不含时间项反映了状态不会改变的事实。

自然的，这类二值估计问题可以利用离散贝叶斯滤波来处理。但是，置信度通常由一个概率比的对数(log odds ratio) 来实现。

状态$x$的概率(odds) 定义为此事件的概率除以该事件不发生的概率
$$\frac{p(x)}{p(x^{\prime })}=\frac{p(x)}{1-(x)}$$

概率对数就是这个表达式的对数
$$l(x):=log\frac{p(x)}{1-p(x)}$$
概率对数假设值为$-\infty \sim \infty$ 。用于更新以概率对数表示的置信度的贝叶斯滤波计算很简洁。它避免了概率接近0 或1 引起的截断间题。

程序给出了其基本的更新算法。这种算法是加法。事实上，任何对测量做出反应的变量的递增和递减都可以解释为贝叶斯滤波的概率对数形式。该二值
贝叶斯滤波利用一个反向测量模型(inverse measurement model) $p(x|z_t)$代替熟悉的前向模型$p(z_t|x)$ 。反向测量模型将关于（二值）状态变量的一个分布指定为测量$z_t$的一个函数。

反向模型经常用于测量比二值状态更复杂的情况。这种情况的一个实例就是
从相机图像中估计门是否为关的问题。这里状态很简单，但需要进行所有测量的空间却是很大的。 通过设计一个函数根据相机图像来计算门为关着的概率，要比描述所有相机图像中显示门为关着的分布更容易些。 换句话说，实现一个反向传感器模型比前向传感器模型更容易。

置信度$be{l}_t(x)$ 可以根据概率比对数$l_t$ 通过下面的方程来求得：
$$be{l}_t(x)=1-\frac{1}{1+e^{l_t}}$$
为了证明二值贝叶斯滤波算法的正确性，简要重申基本的贝叶斯滤波方程，并明确的贝叶斯归一化方法：
$$\begin{gathered} p(x|z_{1:t})=\frac{p(z_t|x,z_{1:t-1})p(x|z_{1:t-1})}{p(z_t|z_{1:t-1})} \\ =\frac{p(z_t|x)p(x|z_{1:t-1})}{p(z_t|z_{1:t-1})} \end{gathered}$$
现在将贝叶斯准则应用于测量模型$p(z_t|x)$:
$$p(z_t|x)=\frac{p(x|z_t)p(z_t)}{p(x)}$$
同时得到
$$p(x|z_{1:t})=\frac{p(x|z_t)p(z_t)p(x|z_{1:t-1})}{p(x)p(z_t|z_{1:t-1})}\text{\hspace{1em}(7.1)}$$
用类似的方法，得出对立事件$x^{\prime }$:
$$p(x^{\prime }|z_{1:t})=\frac{p(x^{\prime }|z_t)p(z_t)p(x^{\prime }|z_{1:t-1})}{p(x^{\prime })p(z_t|z_{1:t-1})}\text{\hspace{1em}(7.2)}$$
用式(2) 除以式(1) 可以将各种难以计算的概率抵消：
$$\begin{gathered} \frac{p(x|z_{1:t})}{p(x^{\prime }|z_{1:t})}=\frac{p(x|z_t)}{p(x^{\prime }|z_t)}\frac{p(x|z_{1:t-1})}{p(x^{\prime }|z_{1:t-1})}\frac{p(x^{\prime })}{p(x)} \\ =\frac{p(x|z_t)}{1-p(x|z_t)}\frac{p(x|z_{1:t-1})}{1-p(x|z_{1:t-1})}\frac{1-p(x)}{p(x)}\text{\hspace{1em}(7.3)} \end{gathered}$$
用以$l_t(x)$ 表示置信度$be{l}_t(x)$ 的概率比对数。时刻$t$ 的置信度概率对数由式(3) 的对数给出：
$$\begin{gathered} l_t(x)=\log \frac{p(x|z_t)}{1-p(x|z_t)}+\log \frac{p(x|z_{1:t-1})}{1-p(x|z_{1:t-1})}+\log \frac{1-p(x)}{p(x)} \\ =\log \frac{p(x|z_t)}{1-p(x|z_t)}-\log \frac{1-p(x)}{p(x)}+l_{t-1}(x)\text{\hspace{1em}(7.4)} \end{gathered}$$
这里$p(x)$是状态$x$ 的先验(prior) 概率。在式(4) 中，每个测最更新涉及先验（以概率对数形式）的求和。先验也定义为处理传感器测量前的初始置信度的概率对数：
$$l_0(x)=\log \frac{p(x)}{1-p(x)}\text{\hspace{1em}(7.5)}$$

3.二值贝叶斯滤波算法

输入

二进制贝叶斯滤波器算法计算由l t表示的后置置信度的对数几率。
最初，滤波器将置信度t-1和测量值z t的先前对数比值比作为参数。

计算方式

然后，过滤器通过将先验概率 lt-1加到对数比值的反向测量模型$log\frac{p（x|z_t）}{1-p（x|z_t）}$中，并减去初始概率也已知的初始概率$log\frac{p（x）}{1-p（x）}$，来计算系统lt的=新后验概率。初始置信度代表在考虑任何传感器测量值之前系统的初始状态。

输出

最后，算法返回系统$l_t$的后验概率，开始新的迭代周期。

八、占用栅格地图构建算法推导

许多占用栅格地图构建算法的黄金定律是根据给定的数据计算整个地图的后
验概率。
$$p(m|z_{1:t},x_{1:t})\text{\hspace{1em}(8.1)}$$
式中， $m$ 为地图； $z_{1:t}$ 为直到时刻t 的所有测量值； $x_{1:t}$ 为用所有机器人位姿定义的路径。由于路径是已知的，因此，控制$u_{1:t}$ 在占用栅格地图中不充当角色。所以，这个部分会忽略掉。

被占用栅格地图所考虑的一类地图，应在连续位置空间上定义了精细粒度栅
格的。到目前为止，最常用的占用栅格地图是二维平面地图，这类二维平面地图描述的是三维世界的二维切片。二维地图通常是机器人平面导航的选择，这些机器入装备了传感器仅能感知世界的切片。占用栅格地图技术可以推广到三维，但是计算量非常大。

$m_i$表示第$i$ 个栅格单元，占用棚格地图将空间分割为有限多个栅格单元。
$$m=m_i\text{\hspace{1em}(8.2)}$$
每个$m_i$ 与一个二值占用变量相对应，该变量指示出该单元是否被占用。如果该栅格被占用为"1", 未被占用为"0" 。$p(m_i=1)$ 或$p(m_i)$ 表示了该栅格单元被占用的可能性。

式(8. 1) 中的后验概率的问题是它的维数。如图所示的地图有上万个栅
格单元。对千一个有10 000 个栅格单元的地图，不同地图的可能性会有$2^{10000}$种。对每一个地图计算后验概率简直不可想象。

标准的占用栅格方法将构建地图这一问题划分为一些独立的间题，即为所有
的栅格单元m建立后验概率：
$$p(m_i|z_{1:t},x_{1:t})\text{\hspace{1em}(8.3)}$$
每一个这样的问题都是一个静态的二值间题。这样的分解是非常方便的，但不是没有问题。具体来说，这种方法使得不能表达相邻单元之间的联系；相反，整个地图的后验概率用边缘概率的乘积近似。
$$p(m|z_{1:t},x_{1:t})=\prod p(m_i|z_{1:t},x_{1:t})\text{\hspace{1em}(8.4)}$$

幸亏有了这个因式分解，每个栅格单元的占用概率现在是一个静态二值估计
问题。关于该问题的滤波器是二值贝叶斯滤波器(the binary Bayesfilter) 。

该算法将该滤波器应用于占用栅格地图构建问题。如同原来的滤波器一样，这里的占用栅格地图构建算法应用了对数占用概率表达方式，即
$$l_{t,i}=\log \frac{p(m_i|z_{1:t},x_{1:t})}{1-p(m_i|z_{1:t},x_{1:t})}\text{\hspace{1em}(8.5)}$$
对数概率表达的优点是可以避免0 和1 附近数值的不稳定性。由此计算后验概率为
$$p(m_i|z_{1:t},x_{1:t})=1-\frac{1}{1+exp\{l_{t,i}\}}\text{\hspace{1em}(8.6)}$$
上述伪代码给出的occupancy_grid_mapping 算法遍历所有的栅格单元$i$, 并更新所有传感器测量锥内的测量值$z_t$ 。对于传感器测量锥内的栅格单元，用第4 行中函数inverse—sensor—model 的结果来更新占用值。否则，占用值保持不变，如第6行所示。常数$l_0$是用对数让步比所表示的先验占用概率，即
$$l_0=\log \frac{p(m_i=1)}{p(m_i=0)}=\log \frac{p(m_i)}{1-p(m_i)}\text{\hspace{1em}(8.7)}$$
函数inverse_ sensor_ model 应用了反演测量模型$p(m_i|z_t,x_t)$ 的对数型式，即
$$inverse\_sensor\_model(m_i,x_i,z_t)=\log \frac{p(m_i|z_t,x_t)}{1-p(m_i|z_t,x_t)}\text{\hspace{1em}(8.8)}$$

一个简单的inverse_range_sensor_model模型给传感器测量锥中的每个栅格分配一个占用值$l_{occ}$ 。在下面伪代码中，该区域的宽度由参数$\alpha$ 控制，波束角由参数$\beta$ 给出。可以看到，该参数有点简单；当前应用的占用栅格概率在测量锥边缘通常会更加脆弱。

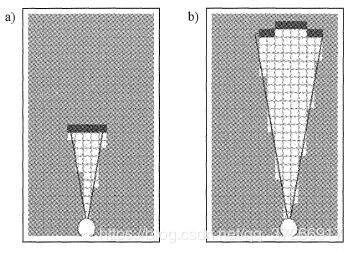
每个栅格中的暗度对应该栅格被占用的可能性；该模型有点过于简单，目前应用的占用栅格概率算法通常会在测量锥的边缘过于脆弱。

函数Inverse_range_sensor_model 通过首先确定波束索引$k$ 和单元$m_i$中心的测量距离$r$来计算反演模型。该计算由程序第2~5行完成。

通常，假设机器入的位姿为$x_t=（x,y,\theta {）}^T$。

在第7 行，当某单元在传感器波束测量范围之外时或该单元位于测量距离$z_t^k$后面超过$\alpha /2$ 时，返回对数形式的占用先验概率。

在第9行，如果单元的距离在探查范围$z_t^k$的$\pm \alpha /2$以内，返回$l_{occ}>l_0。$

如果单元的距离比测量距离短$\alpha /2$ 还多，返回$l_{free}<l_0$。

反演超声波传感器模型的典型应用如下图所示。从原始地图开始机器人成
功地通过吸收由反演模型生成的局部地图扩展了地图。

九、占用栅格地图构建算法

占用栅格映射算法$(\{I_{t-1,i}\}\{x_t\}\{z_t\})$:
$\{I_{t-1,i}\}$：先验概率
$\{x_t\}$：位置
$\{z_t\}$：测量值

占用网格映射算法实现了二进制Bayes滤波器来估计每个单元的占用值。

最初，该算法将姿势和测量值的单元格的先前占用值作为占用栅格图的参数。

现在如果测距仪传感器当前正在感测这些单元以更好地了解这种情况，则算法会测试每个单元的所有网格单元之间的循环关系。

让我们在这里看这个例子

一个移动机器人在感应环境，该区域处于测量锥下，并以白色和黑色突出显示。当遍历所有单元格时，算法会将那些白色和黑色单元格视为属于测量的感知范围内的单元格。

现在，该算法将通过使用二进制基本滤波器算法计算它们的新置信度来更新属于测量锥的单元。

如先前在二进制贝叶斯滤波器算法中所见，通过将先验概率添加到逆传感器模型中来计算单元的新状态。逆传感器模型表示给出测量并反对的后部地图概率的锁定奇数比。并减去对数比值形式的初始状态（即地图的初始状态）。

对于不属于测量锥范围的单元，其占用率保持不变。现在，该算法将返回单元格的更新占用率值，并开始另一个迭代周期。

十、反向传感器模型

反向传感器模型的符号摘要：

$m_i$：映射即时i或正在处理的当前单元格
$x_i,y_i$：当前单元格的质心
$r$：相对于机器人姿态和质心计算出的质心范围
$k$：相对于机器人姿态（$x，y，\theta$），质心$（x_i，y_i）$和传感器角度而言，与要计算的单元格最匹配的声纳测距仪锥体。
$\beta$：由测量光束形成的圆锥形区域的张角。
$\alpha$：障碍物的宽度等于单元格的大小。请注意，$\alpha$不是视频中提到的圆锥形区域的宽度，而是单元格的宽度。

十一、程序实例

在这个实例中，一个配备了八个声纳测距传感器的机器人在一个环境中循环来绘制它的地图。每个时间戳都为这个机器人提供了精确的姿态。

数据文件

1. measurement.txt:安装在机器人上的声纳测距仪传感器在413秒内记录下每个时间戳的测量值。 (timestamp, measurement 1:8)。
2. poses.txt:在413秒的时间内，机器人在每个时间戳上都能准确地摆出各种姿势。(timestamp, x, y, ϴ)

全局函数

1. inverseSensorModel()
2. occupancyGridMapping()

主函数

1. File Scan:扫描测量和姿势文件以检索值。在每个时间戳处，这些值都将传递到占用网格映射功能。
2. Display Map: 处理完所有测量值和姿势后，将显示地图。

#include 
#include 
#include 
using namespace std;

// Sensor characteristic: Min and Max ranges of the beams
double Zmax = 5000, Zmin = 170;
// Defining free cells(lfree), occupied cells(locc), unknown cells(l0) log odds values
double l0 = 0, locc = 0.4, lfree = -0.4;
// Grid dimensions
double gridWidth = 100, gridHeight = 100;
// Map dimensions
double mapWidth = 30000, mapHeight = 15000;
// Robot size with respect to the map 
double robotXOffset = mapWidth / 5, robotYOffset = mapHeight / 3;
// Defining an l vector to store the log odds values of each cell
vector< vector<double> > l(mapWidth/gridWidth, vector<double>(mapHeight/gridHeight));

double inverseSensorModel(double x, double y, double theta, double xi, double yi, double sensorData[])
{
    //******************Code the Inverse Sensor Model Algorithm**********************//
    // Defining Sensor Characteristics
    double Zk, thetaK, sensorTheta;
    double minDelta = -1;
    double alpha = 200, beta = 20;

    //******************Compute r and phi**********************//
    double r = sqrt(pow(xi - x, 2) + pow(yi - y, 2));
    double phi = atan2(yi - y, xi - x) - theta;

    //Scaling Measurement to [-90 -37.5 -22.5 -7.5 7.5 22.5 37.5 90]
    for (int i = 0; i < 8; i++) {
        if (i == 0) {
            sensorTheta = -90 * (M_PI / 180);
        }
        else if (i == 1) {
            sensorTheta = -37.5 * (M_PI / 180);
        }
        else if (i == 6) {
            sensorTheta = 37.5 * (M_PI / 180);
        }
        else if (i == 7) {
            sensorTheta = 90 * (M_PI / 180);
        }
        else {
            sensorTheta = (-37.5 + (i - 1) * 15) * (M_PI / 180);
        }

        if (fabs(phi - sensorTheta) < minDelta || minDelta == -1) {
            Zk = sensorData[i];
            thetaK = sensorTheta;
            minDelta = fabs(phi - sensorTheta);
        }
    }

    //******************Evaluate the three cases**********************//
    if (r > min((double)Zmax, Zk + alpha / 2) || fabs(phi - thetaK) > beta / 2 || Zk > Zmax || Zk < Zmin) {
        return l0;
    }
    else if (Zk < Zmax && fabs(r - Zk) < alpha / 2) {
        return locc;
    }
    else if (r <= Zk) {
        return lfree;
    }
}

void occupancyGridMapping(double Robotx, double Roboty, double Robottheta, double sensorData[])
{
    for (int x = 0; x < mapWidth / gridWidth; x++) {
        for (int y = 0; y < mapHeight / gridHeight; y++) {
            double xi = x * gridWidth + gridWidth / 2 - robotXOffset;
            double yi = -(y * gridHeight + gridHeight / 2) + robotYOffset;
            if (sqrt(pow(xi - Robotx, 2) + pow(yi - Roboty, 2)) <= Zmax) {
                l[x][y] = l[x][y] + inverseSensorModel(Robotx, Roboty, Robottheta, xi, yi, sensorData) - l0;
            }
        }
    }
}

int main()
{
    double timeStamp;
    double measurementData[8];
    double robotX, robotY, robotTheta;

    FILE* posesFile = fopen("poses.txt", "r");
    FILE* measurementFile = fopen("measurement.txt", "r");

    // Scanning the files and retrieving measurement and poses at each timestamp
    while (fscanf(posesFile, "%lf %lf %lf %lf", &timeStamp, &robotX, &robotY, &robotTheta) != EOF) {
        fscanf(measurementFile, "%lf", &timeStamp);
        for (int i = 0; i < 8; i++) {
            fscanf(measurementFile, "%lf", &measurementData[i]);
        }
        occupancyGridMapping(robotX, robotY, (robotTheta / 10) * (M_PI / 180), measurementData);
    }
    
    // Displaying the map
    for (int x = 0; x < mapWidth / gridWidth; x++) {
        for (int y = 0; y < mapHeight / gridHeight; y++) {
            cout << l[x][y] << " ";
        }
    }
    
    return 0;
}

十二、地图构建

从GitHub下载

$ cd /home/workspace/
$ git clone https://github.com/udacity/RoboND-OccupancyGridMappingAlgorithm

接下来，编辑 main.cpp

#define _USE_MATH_DEFINES
#include 
#include 
#include 
using namespace std;

// 传感器特性：光束的最小和最大范围
double Zmax = 5000, Zmin = 170;
// 定义空单元格（free），占用单元格（locc），未知单元格（l0）的对数比值
double l0 = 0, locc = 0.4, lfree = -0.4;
// Grid dimensions
double gridWidth = 100, gridHeight = 100;
// Map dimensions
double mapWidth = 30000, mapHeight = 15000;
// 机器人相对于地图的大小 
double robotXOffset = mapWidth / 5, robotYOffset = mapHeight / 3;
// 定义一个向量来存储每个像元的对数比值
vector< vector<double> > l(mapWidth / gridWidth, vector<double>(mapHeight / gridHeight));

double inverseSensorModel(double x, double y, double theta, double xi, double yi, double sensorData[])
{
    //******************Code the Inverse Sensor Model Algorithm**********************//
    // Defining Sensor Characteristics
    double Zk, thetaK, sensorTheta;
    double minDelta = -1;
    double alpha = 200, beta = 20;

    double r = sqrt(pow(xi - x, 2) + pow(yi - y, 2));
    double phi = atan2(yi - y, xi - x) - theta;

    //将测量缩放到 [-90 -37.5 -22.5 -7.5 7.5 22.5 37.5 90]
    for (int i = 0; i < 8; i++) {
        if (i == 0) {
            sensorTheta = -90 * (M_PI / 180);
        }
        else if (i == 1) {
            sensorTheta = -37.5 * (M_PI / 180);
        }
        else if (i == 6) {
            sensorTheta = 37.5 * (M_PI / 180);
        }
        else if (i == 7) {
            sensorTheta = 90 * (M_PI / 180);
        }
        else {
            sensorTheta = (-37.5 + (i - 1) * 15) * (M_PI / 180);
        }

        if (fabs(phi - sensorTheta) < minDelta || minDelta == -1) {
            Zk = sensorData[i];
            thetaK = sensorTheta;
            minDelta = fabs(phi - sensorTheta);
        }
    }

    //******************Evaluate the three cases**********************//
    // 在测量锥外的都认为是未知单元格
    if (r > min((double)Zmax, Zk + alpha / 2) || fabs(phi - thetaK) > beta / 2 || Zk > Zmax || Zk < Zmin) {
        return l0;
    }
    // 在测量处认定为占用单元格
    else if (Zk < Zmax && fabs(r - Zk) < alpha / 2) {
        return locc;
    }
    // 在测量锥内且小于测量值处认为是空单元格
    else if (r <= Zk) {
        return lfree;
    }
}

void occupancyGridMapping(double Robotx, double Roboty, double Robottheta, double sensorData[])
{
    //1 - TODO: Generate a grid (size 300x150) and then loop through all the cells
    //2 - TODO: Compute the center of mass of each cell xi and yi 
            //double xi = x * gridWidth + gridWidth / 2 - robotXOffset;
            //double yi = -(y * gridHeight + gridHeight / 2) + robotYOffset;
    //3 - TODO: Check if each cell falls under the perceptual field of the measurements
    for (int x = 0; x < mapWidth / gridWidth; x++) {
        for (int y = 0; y < mapHeight / gridHeight; y++) {
            double xi = x * gridWidth + gridWidth / 2 - robotXOffset;
            double yi = -(y * gridHeight + gridHeight / 2) + robotYOffset;
            if (sqrt(pow(xi - Robotx, 2) + pow(yi - Roboty, 2)) <= Zmax) {
                l[x][y] = l[x][y] + inverseSensorModel(Robotx, Roboty, Robottheta, xi, yi, sensorData) - l0;
            }
        }
    }
}


void visualization()
{
    //TODO: Initialize a plot named Map of size 300x150
    //Graph Format
    plt::title("MCG image");
    plt::xlim(0, 300);
    plt::ylim(0, 150);
    //TODO: Loop over the log odds values of the cells and plot each cell state. 
    //Unkown state: green color, occupied state: blue color, and free state: red color 

    for (double x = 0; x < mapWidth / gridWidth; x++) {
        for (double y = 0; y < mapHeight / gridHeight; y++) {
            if (l[x][y] == 0) {
                plt::plot({ x }, { y }, "g.");
            }
            else if (l[x][y] > 0) {
                plt::plot({ x }, { y }, "b.");
            }
            else {
                plt::plot({ x }, { y }, "y.");
            }
        }
    }

    //Save the image and close the plot
    plt::save("./Images/MCG_Map.png");
    plt::clf();
}


int main()
{
    double timeStamp;
    double measurementData[8];
    double robotX, robotY, robotTheta;

    FILE* posesFile = fopen("poses.txt", "r");
    FILE* measurementFile = fopen("measurement.txt", "r");

    // 扫描文件并获取每个时间戳的测量值和姿势
    while (fscanf(posesFile, "%lf %lf %lf %lf", &timeStamp, &robotX, &robotY, &robotTheta) != EOF) {
        fscanf(measurementFile, "%lf", &timeStamp);
        for (int i = 0; i < 8; i++) {
            fscanf(measurementFile, "%lf", &measurementData[i]);
        }
        occupancyGridMapping(robotX, robotY, (robotTheta / 10) * (M_PI / 180), measurementData);
    }

    // 显示地图
    cout << "Wait for the image to generate" << endl;
    visualization();
    cout << "Done!" << endl;

    return 0;
}

然后，编译程序

$ cd RoboND-OccupancyGridMappingAlgorithm/
$ rm -rf Images/* 
$ g++ main.cpp -o app -std=c++11 -I/usr/include/python2.7 -lpython2.7

最后运行程序

$ ./app

生成结果如下

十三、多传感器信息融合

机器人常装备不止一种的传感器。因此，就需要将多种传感器信息融合进一
个地图。如果传感器具有不同的特性，关于如何将多种传感器的数据进行融合的问题会非常有趣。例如，由立体视觉系统构建的占用栅格地图， 影像差异被投影到平面上并用高斯卷积。很明显，该立体视觉系统不同于超声波测距传感器。它们对不同种类的障碍物敏感。

不幸的是，将多种传感器数据用贝叶斯滤波器融合不是一件容易的事。简单
的解决办法是，对不同的传感器模式执行occupancy_grid_mapping算法。

但是，这种方法有一个明显的缺点。如果不同的传感器探测到不同种
类的障碍物，贝叶斯传感器的结果就会不清楚。

试想一下，例如，一个障碍物可以由一种传感器识别，但不能被另一种传感器识别。那么这两种传感器生成的互相矛盾的信息，会导致最终的地图依赖每个传感器系统提供的证据的数量。这是非常讨厌的，因为一个单元是否被认为是被占用得依赖不同传感器投票的频率。

将不同传感器信息进行融合的方法，通常是对每种传感器建立各自的地图，再用合适的方法将这些地图融合。设$m^k=\{m_i^k\}$门，表示地图是由第$k$种传感器生成的。如果传感器测量值不互相依赖，那么就可以直接用德· 摩根定律(DeMorgan’s law) 将其分解：
$$p(m_i)=1-\prod (1-p(m_i^k))$$

另外，这里还可以对所有的地图计算最大值：
$$p(m_i)=\max p(m_i^k)$$
这些地图生成关于该单元的最悲观的估计。如果某种具体的传感器地图认为
某栅格被占用，那么融合地图也会这样认为。

例如有两个地图如下$map1=\left[\begin{array}{cc}0.9& 0.6\\ 0.1& 0.5\end{array}\right]$,$map2=\left[\begin{array}{cc}0.3& 0.4\\ 0.4& 0.3\end{array}\right]$

我们将两个地图整合在一起

#include 
#include 
using namespace std;

const int mapWidth =  2;
const int mapHeight = 2;

void sensorFusion(double m1[][mapWidth], double m2[][mapWidth])
{
    for (int x = 0; x < mapHeight; x++) {
        for (int y = 0; y < mapWidth; y++) {
            double p = 1 - (1 - m1[x][y]) * (1 - m2[x][y]);
            cout << p << " ";
        }
        cout << endl;
    }
}

int main()
{

    double m1[mapHeight][mapWidth] = { { 0.9, 0.6 }, { 0.1, 0.5 } };
    double m2[mapHeight][mapWidth] = { { 0.3, 0.4 }, { 0.4, 0.3 } };
    sensorFusion(m1, m2);

    return 0;
}

输出为

0.93 0.76
0.46 0.65