day07_原题100/104/107/111/168/172
1.Excel表列序号(原题168)
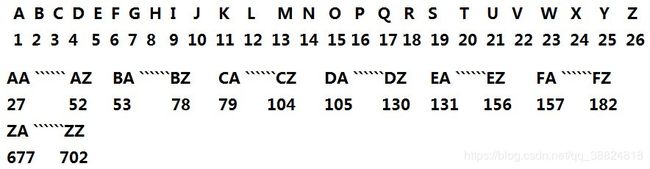
给定一个Excel表格中的列名称,返回其相应的列序号.
例如,
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
示例 1:
输入: "A"
输出: 1
示例 2:
输入: "AB"
输出: 28
示例 3:
输入: "ZY"
输出: 701
(1)思路:
这道题有点类似整数转罗马数字题,思路是先将数字对26整除,若余数不为0则说明是前25个字母中的任意一个;若余数为0,说明是Z,下一次进行循环判断之前需要先减去一个数再取余
(2)代码:
class Solution:
def convertToTitle(self, n: int) -> str:
dict = {1: "A", 2: "B", 3: "C", 4: "D", 5: "E", 6: "F", 7: "G", 8: "H", 9: 'I', 10: "J", 11: "K", 12: "L",
13: "M", 14: "N", 15: "O", 16: "P", 17: "Q", 18: "R", 19: "S", 20: "T", 21: "U", 22: "V", 23: "W",
24: "X", 25: "Y", 26: "Z"}
res = ""
while n > 0:
res += dict[n % 26]
if n % 26: # 余数是0,说明是 Z
n //= 26
else:
n = (n-26) // 26 # 余数为0时,需要先减26再进行下次取余
return res[::-1]
2.阶乘后的零(原题172)
给定一个整数 n,返回 n! 结果尾数中零的数量
示例 1:
输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
(1)思路:
这个貌似就是数学分析的题目,每个2和5提供一个10,而每5个数当中必然有一个2,因此只需要分析5的数量有多少
(2)代码:
# 方法一
class Solution:
def trailingZeroes(self, n: int) -> int:
res = 0
while n > 0:
n //= 5
res += n
return res
# 方法二
class Solution:
def trailingZeroes(self, n: int) -> int:
if n < 5:
return 0
x,y = 5,0
while x <= n:
y += n // x
x *= 5
return y
3.相同的树(原题100)
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ \ / \
2 3 2 3
[1,2,3], [1,2,3]
输出: true
示例 2:
输入: 1 1
/ \
2 2
[1,2], [1,null,2]
输出: false
示例 2:
输入: 1 1
/ \ / \
2 1 1 2
[1,2,1], [1,1,2]
输出: false
(1)思路:
首先判断两棵树的值是否有一方为空,若有,则报错;然后判断两棵树的值是否相等,不相等则报错;最后对两棵树结构上及其节点上的值进行判断,若都相同则返回True
(2)代码:
class Solution:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
if p == None and q == None:
return True
if p == None and q != None:
return False
if p != None and q == None:
return False
if p.val != q.val:
return False
return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
4.二叉树的最大深度(原题104)
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
(1)思路:
主要是使用DFSC策略,不断访问根节点
(2)代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if root == None:
return 0
else:
left_height = self.maxDepth(root.left)
right_height = self.maxDepth(root.right)
return max(left_height,right_height)+1
# 写法二;
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if root == None:
return 0
left = maxDepth(root.left)
right = maxDepth(root.right)
return max(left,right)+1
# 写法三:
class Solution:
def maxDepth(self, root: TreeNode) -> int:
return root == Null ? 0:max(maxDepth(root.left),maxDepth(root.right))+1
5.二叉树最小深度(原题111)
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最小深度 2.
(1)思路:
思路是和上题一样的,具体分析见上图
(2)代码:
- 下面是不通过的代码,对于[1,2]这个测试用例,最小深度是2,而不是1.果然掉坑
class Solution:
def minDepth(self, root: TreeNode) -> int:
if root == None:
return 0
left = minDepth(root.left)
right = minDepth(root.right)
return min(left,right)+1
- 修改
class Solution:
def minDepth(self, root: TreeNode) -> int:
if root == None:
return 0
if root.left == None:
return self.minDepth(root.right)+1
if root.right == None:
return self.minDepth(root.left)+1
return min(self.minDepth(root.left),self.minDepth(root.right))+1
6.二叉树层次遍历II(原题107)
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其自底向上的层次遍历为:
[
[15,7],
[9,20],
[3]
]
(1)思路:
如图所示,层次遍历原理:
-
根结点 1 出队,出队的同时,将左孩子 2 和右孩子 3 分别入队;
-
队头结点 2 出队,出队的同时,将结点 2 的左孩子 4 和右孩子 5 依次入队;
-
队头结点 3 出队,出队的同时,将结点 3 的左孩子 6 和右孩子 7 依次入队;
-
不断地循环,直至队列内为空。
(2)代码:
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
result = []
outlist = [root]
while outlist:
newlist = []
newlevel = []
for element in outlist:
if element:
newlevel.append(element.val)
newlist.append(element.left)
newlist.append(element.right)
outlist = newlist
if newlevel:
result.append(newlevel)
retun result[::-1]