华泰单因子测试之估值类因子（分层回测）
分层回测
'''
class FactorAnalyzer(object):
def __init__(self, factor, prices, groupby=None, weights=1.0,
quantiles=None, bins=None, periods=(1, 5, 10),
binning_by_group=False, max_loss=0.25, zero_aware=False)
'''
api = data.DataApi(fq='pre', industry='jq_l1', weight_method='ln_mktcap')
api.auth('', '')
pe_factor = analyze.FactorAnalyzer(factor_data,prices=api.get_prices,groupby=api.get_groupby,\
weights=api.get_weights,bins=5,periods=(1,10,20))1)其中binning_by_group参数至关重要
- 若binning_by_group=Flase，则按[日期]分组计算因子分位数，计算完因子分位数后，按[因子分位数]groupby(level=['date', 'factor_quantile'])分组计算权重。
- 若binning_by_group=True,则按照[日期，行业]分组计算因子分位数，计算完因子分位数后，按[因子分位数]groupby(level=['date', 'factor_quantile'])分组计算权重。
所以binning_by_group参数即影响了因子分位数factor_quantile也影响了权重weights
2）市值对估值因子有显著的影响（jqfactor_analyaer没法做到按市值对因子值分层）
3)行业选择问题
申万一级行业又28个，假设分5层，对于中证500来说，每行业每层也就3~4只股票，每层中股票数量太少，不够严谨。觉得可以使用聚宽一级行业（11个）对行业进行划分。
4）因子值怎么分层很重要。jqfactor_analyzer中因子值分层有两种方法。
- quantiles : int or sequence[float]
在因子分组中按照因子值大小平均分组的组数。
或分位数序列, 允许不均匀分组
例如 [0, .10, .5, .90, 1.] 或 [.05, .5, .95]
'quantiles' 和 'bins' 有且只能有一个不为 None
- bins : int or sequence[float]
在因子分组中使用的等宽 (按照因子值) 区间的数量
或边界值序列, 允许不均匀的区间宽度
例如 [-4, -2, -0.5, 0, 10]
'quantiles' 和 'bins' 有且只能有一个不为 None
一、因子收益
- 绘制各分位数各周期的平均收益（收益数值不是重点，主要用于观察是否具有单调性）
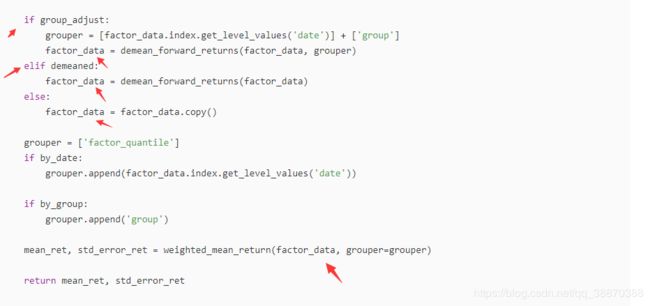
pe_factor.plot_quantile_returns_bar(by_group=False, demeaned=False, group_adjust=False)
仔细解读各个参数的作用：
- group_adjust和demeaned有且仅有一个参数起作用。
- group_adjust和demeaned会影响factor_date。group_adjust：按[日期，行业]分组对因子远期收益去均值。demeaned：按[日期]分组对因子远期收益去均值。
- by_group并不会影响factor_data，只会影响函数weighted_mean_return中的分组。
这说明：调用函数rate_of_return(转换回报率为"每期"回报率：如果收益以稳定的速度增长, 则相当于每期的回报率）计算每天收益率。
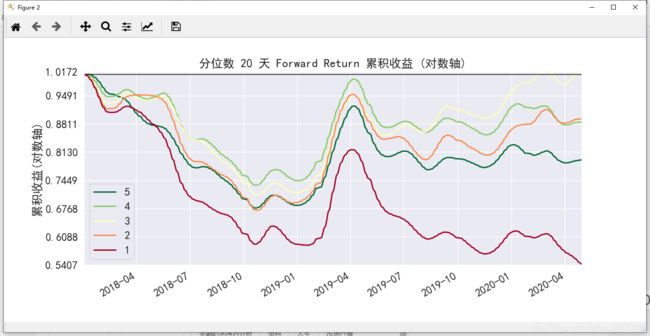
2、 绘制各分位数的累计收益（收益数值不是重点，看层次是否分明）
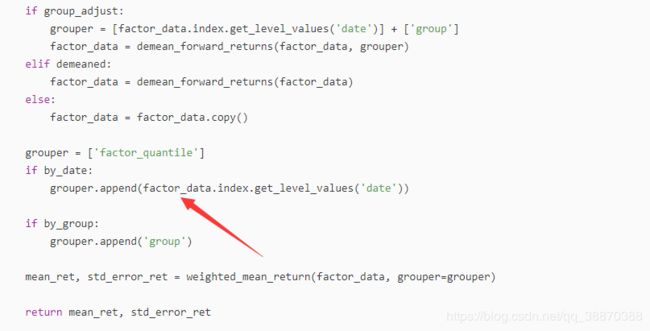
pe_factor.plot_cumulative_returns_by_quantile(period=20, demeaned=False, group_adjust=False)
解读：
- 参数by_date=True,by_group_False已经默认。所以函数weighted_mean_return是按[日期]分组计算收益的。
这里并没有使用rate_of_return函数
3、分层收益
1）分维度获得 因子收益和标准差
mean_return_by_quantile = pe_factor.calc_mean_return_by_quantile(by_date=1, by_group=0, \
demeaned=0, group_adjust=0) def calc_mean_return_by_quantile(self, by_date=False, by_group=False,
demeaned=False, group_adjust=False):
"""计算按分位数分组因子收益和标准差
因子收益为收益按照 weight 列中权重的加权平均值
参数:
by_date:
- True: 按天计算收益
- False: 不按天计算收益
by_group:
- True: 按行业计算收益
- False: 不按行业计算收益
demeaned:
- True: 使用超额收益计算各分位数收益，超额收益=收益-基准收益
(基准收益被认为是每日所有股票收益按照weight列中权重的加权的均值)
- False: 不使用超额收益
group_adjust:
- True: 使用行业中性收益计算各分位数收益，行业中性收益=收益-行业收益
(行业收益被认为是每日各个行业股票收益按照weight列中权重的加权的均值)
- False: 不使用行业中性收益
"""
return pef.mean_return_by_quantile(self._clean_factor_data,
by_date=by_date,
by_group=by_group,
demeaned=demeaned,
group_adjust=group_adjust)注意： 没有使用rate_of_return函数
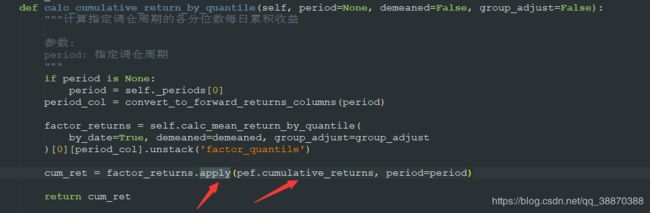
2）计算指定调仓周期的各分位数每日累积收益
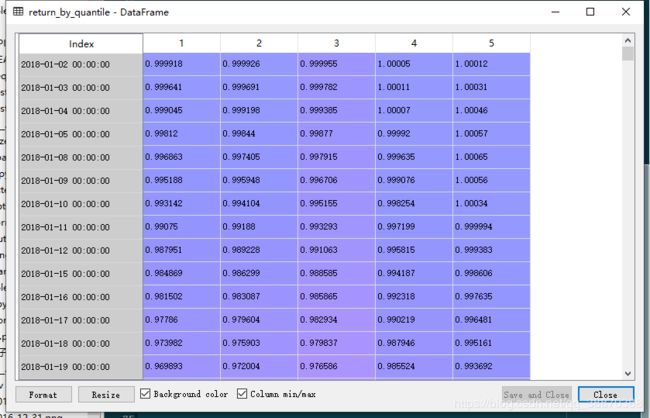
return_by_quantile = pe_factor.calc_cumulative_return_by_quantile(period=20,\
demeaned=False, group_adjust=False)
def cumulative_returns(returns, period):
"""
从'N 期'因子远期收益率构建累积收益
当 'period' N 大于 1 时, 建立平均 N 个交错的投资组合 (在随后的时段 1,2,3，...，N 开始),
每个 N 个周期重新调仓, 最后计算 N 个投资组合累积收益的均值。
参数
----------
returns: pd.Series
N 期因子远期收益序列
period: integer
对应的因子远期收益时间跨度
返回值
-------
pd.Series
累积收益序列
"""
returns = returns.fillna(0)
if period == 1:
return returns.add(1).cumprod() #cumprod:累乘
#
# 构建 N 个交错的投资组合
#
def split_portfolio(ret, period):
return pd.DataFrame(np.diag(ret))
sub_portfolios = returns.groupby(
np.arange(len(returns.index)) // period, axis=0
).apply(split_portfolio, period)
sub_portfolios.index = returns.index
#
# 将 N 期收益转换为 1 期收益, 方便计算累积收益
#
def rate_of_returns(ret, period):
#列中包含数据元素、NaN元素，将列相加，使结果等于数据
return ((np.nansum(ret) + 1)**(1. / period)) - 1注：是按上面的方法计算累计收益的
3）指标计算
