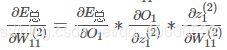tensorflow入门:利用全连接神经网络实现手写数字识别(一)
一、简介
全连接神经网络可简单理解为每一个节点都互相连接。如下图
![]()
程序实现的基本思想是:通过提取图片特征作为输入向量,通过前向传播算法得到输出向量,再通过反向传播算法更新权重W和偏置b,不断训练得到最优解。
二、前向传播算法
前向传播可以简单地理解为从输入到输出的计算过程。
计算前向传播结果需要三部分信息:
1、神经网络的输入
即输入特征向量x1、x2等,在手写数字识别中输入向量大小为28*28=784的矩阵(28*28为每个训练图片的分辨率大小)
2、神经网络的结构关系
在全连接神经网络中,结构关系为每一个神经元(节点)之间的输入输出关系,即它们的“边”。
3、每个神经元的参数
用W来表示节点的参数(即权重),b来表示偏置项。W的上标是神经网络的当前层数,下标是两个连接节点的编号。计算方法为加权求和,y=x1*w1+b。
权重是我们运算的一个关系量自然是要有的,而如果没有偏置,函数的线性分类线会通过零点。而在一些分类问题中,通过零点无异于灾难。关于偏置可以看下博文。
https://blog.csdn.net/Uwr44UOuQcNsUQb60zk2/article/details/81074408
激活函数:
在计算后仍然只是一个简单的线性曲线,此时即便有再多的隐藏层,其整个网络跟单层神经网络也是等价的。只有加入了激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。
几个典型的激活函数介绍见以下:
https://blog.csdn.net/u014595019/article/details/52562159?utm_source=blogxgwz0
通过以上条件可以通过前向传播算法得到输出结果y。
二、反向传播算法
通过计算某一参数对损失误差的的影响来更新该参数,具体表现为通过损失函数计算总误差再对参数如w1求偏导。
到此,我们求出了总体误差对相应隐含层的权重W的偏导数。他的含义是在当前位置上,如果权重W移动一小段距离,会引起总体误差的变化的大小。调整参数公式如下
其中η 为学习速率,可以理解为更新参数幅值的大小,如果取得太大会导致怎么更新都无法得到最优解,太小又会更新太慢,通常取较小值或者使用指数衰减的学习率。
三、相关概念
(一)变量(Variables)
1、创建一个变量
state = tf.Variable(0, name="counter")
创建了一个名为state的变量,初始化值为0
2、初始化变量
定义一个初始化节点,初始化图中所有变量
init_op = tf.initialize_all_variables()
(二)常量(constant)
1、创建一个常量
one = tf.constant(1)
注意:常量节点不需要初始化
(三)运算方法
运算方法只是表达式,在真正的session开始run之前,它并不会真正的执行
1、add
功能:将两个Tensor相加
new_value = tf.add(state, one)
2、assign
功能:赋值
update = tf.assign(state, new_value)
将new_value的值赋给state
3、matmul
功能:矩阵相乘
如:
layer2 = tf.matmul(layer1,weights)+biases
4、feed
功能:使用一个tensor值临时替换一个操作的输出结果,并只在调用它的方法内有效,方法结束,临时feed消失。
常用placeholder()占位符为数据“占坑”,如下:
input1 = tf.placeholder(tf.types.float32)
input2 = tf.placeholder(tf.types.float32)
output = tf.mul(input1, input2)
with tf.Session() as sess:
print sess.run([output], feed_dict={input1:[7.], input2:[2.]})
# 输出:# [array([ 14.], dtype=float32)]
利用feed操作形式input1:[7.] 给input1“喂数据”
基本tensorflow搭建神经网络相关理论知识介绍到这里,这里只做初步介绍,具体名词的含义和原理参照其他博文,不当之处希望朋友们及时指出改正~ 下一篇开始介绍如何用python代码实现。