偏微分方程(Partial Differential Equation III)

---

偏微分方程(Partial Differential Equation I)
偏微分方程(Partial Differential Equation II)
偏微分方程(Partial Differential Equation III)
偏微分方程(Partial Differential Equation IV)

---

参考文献：

《数学物理方程》| 季孝达
《数学物理方法》| 吴崇试
《数学物理方法》| 梁昆淼
MOOC北京大学《数学物理方法》| 吴崇试 、高春媛

积分变换法

在积分变换中我们曾用拉普拉斯变换方法求解常微分方程。经过变换，常微分方程变为代数方程，解出代数方程，再进行反演就得常微分方程的解。积分变换在数学物理方程中亦有广泛的应用。

傅里叶变换法

傅里叶变换法常用于求解无界空间（含一维半无界空间）定解问题。本节通过几个例子给出几个重要的解的公式。

Fourier 积分定理：若 $f(x)$ 在 $(-\infty ,+\infty )$上满足：
(1) 在任一有限区间上满足狄利克雷(Dirichlet)条件¹；
(2) 在无限区间 $(-\infty ,+\infty )$上绝对可积，即 ${\int }_{-\infty }^{+\infty }|f(x)|dx$ 收敛
那么，对任意 $x\in (-\infty ,+\infty )$
$$f(x)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }[{\int }_{-\infty }^{+\infty }f(\tau )e^{-ik\tau }\text{d}\tau ]e^{ikx}\text{d}k\text{\hspace{1em}(1.1)}$$
在间断点处，上式左端为 $\frac{1}{2}[f(x^{-})+f(x^{+})]$

Fourier 变换：如果函数 $f(x)$ 满足Fourier 积分定理，由式 (1.1) 知，令
$$F(k)={\int }_{-\infty }^{+\infty }f(x)e^{-ikx}\text{d}x\text{\hspace{1em}(1.2)}$$
则有
$$f(x)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(k)e^{ikx}\text{d}k\text{\hspace{1em}(1.3)}$$
从上面两式可以看出，$f(x)$ 和 $F(k)$ 通过确定的积分运算可以互相转换。 $F(k)$称为 $f(x)$ Fourier 变换(Fourier transform)，或象函数(image function)，记为$F(k)=\mathcal{F}[f(x)]$ ；$f(x)$称为 $F(k)$ Fourier 逆变换(inverse Fourier transform)，或象原函数(original image function)，记为$f(x)={\mathcal{F}}^{-1}[F(k)]$ ；通常称$f(x)$与$F(k)$构成一个Fourier 变换对(transform pair)，记作 $f(x)\leftrightarrow F(k)$ 。

示例：求函数 $f(x)=e^{-b{x}^2}$ 的傅里叶变换，其中常数 $b>0$
解：由定义和分部积分得
$$\begin{array}{rl}F(k)& ={\int }_{-\infty }^{+\infty }f(x)e^{-ikx}dx={\int }_{-\infty }^{+\infty }{e}^{-ikx-b{x}^2}dx\\ & =-\frac{1}{\mathrm{i}k}{e}^{-ikx-b{x}^2}{|}_{-\infty }^{+\infty }-\frac{1}{\mathrm{i}k}{\int }_{-\infty }^{+\infty }2bx{e}^{-ikx-b{x}^2}dx\\ & =\frac{2b\mathrm{i}}{k}\mathcal{F}[xf(x)]=-\frac{2b}{k}\frac{\mathrm{d}}{\mathrm{d}k}F(k)\end{array}$$
取 $k=0$ 可得
$$F(0)={\int }_{-\infty }^{+\infty }{e}^{-b{x}^2}dx=\sqrt{\frac{\pi }{b}}$$
转化为解常微分方程初值问题
$$\{\begin{array}{l}{F}^{\prime }(k)+\frac{k}{2b}F(k)=0\\ F(0)=\sqrt{\frac{\pi }{b}}\end{array}$$
其解为
$$F(k)=\sqrt{\frac{\pi }{b}}\exp (-\frac{k^2}{4b})$$
即
$$\mathcal{F}[e^{-b{x}^2}]=\sqrt{\frac{\pi }{b}}\exp (-\frac{k^2}{4b})(b>0)\text{\hspace{1em}(1.4)}$$
特别的，取 $b=\frac{1}{4c^{2}t}$ 时，有
$$\mathcal{F}[\exp (-\frac{x^2}{4c^{2}t})]=2c\sqrt{\pi t}{e}^{-c^2{k}^{2}t}\text{\hspace{1em}(1.5)}$$
逆变换为
$${\mathcal{F}}^{-1}[e^{-c^2{k}^{2}t}]=\frac{1}{2c\sqrt{\pi t}}\exp (-\frac{x^2}{4c^{2}t})\text{\hspace{1em}(1.6)}$$
由式 (1.4) 还可以得到
$${\int }_0^{+\infty }{e}^{-b{x}^2}\cos kx\mathrm{d}x=\frac{1}{2}\sqrt{\frac{\pi }{b}}\exp (-\frac{k^2}{4b})\text{\hspace{1em}(1.7)}$$
多重傅里叶变换：设 $\mathbf{x}=(x_1,x_2,\cdots ,x_n)\in {\mathbb{R}}^n,\mathbf{k}=(k_1,k_2,\cdots ,k_n),\mathrm{d}\mathbf{x}=d{x}_{1}d{x}_2\cdots d{x}_n$。若 $f(\mathbf{x})$ 在 ${\mathbb{R}}^n$ 上连续，分片光滑且连续可积，令
$$F(\mathbf{k})={\int }_{{\mathbb{R}}^n}f(\mathbf{x})e^{-\mathrm{i}\mathbf{k}\cdot \mathbf{x}}d\mathbf{x}\text{\hspace{1em}(1.8)}$$
则有
$$f(\mathbf{x})=\frac{1}{(2\pi {)}^n}{\int }_{{\mathbb{R}}^n}F(\mathbf{k})e^{\mathrm{i}\mathbf{k}\cdot \mathbf{x}}d\mathbf{k}\text{\hspace{1em}(1.9)}$$
其中 $F(\mathbf{k})$ 称为 $f(\mathbf{x})$ 的 多重傅里叶变换，记为 $F(\mathbf{k})=\mathcal{F}[f(\mathbf{x})]$；$f(\mathbf{x})$ 称为 $F(\mathbf{k})$ 的 多重傅里叶逆变换，记为 $f(\mathbf{x})={\mathcal{F}}^{-1}[F(\mathbf{k})]$

求无限长弦的初值问题
$$\{\begin{array}{l}{u}_{tt}-a^2{u}_{xx}=0\\ u{|}_{t=0}=\varphi (x),\frac{\partial u}{\partial t}{|}_{t=0}=\psi (x)\end{array}$$
其中 $\varphi (x),\psi (x)$ 分别表示初始位移和初始速度。
解：应用傅里叶变换，即方程及初始条件两边同乘以 $e^{-\mathrm{i}kx}$ ，并对空间变量 $x$ 进行积分（时间变量 $t$ 视作参数）。
记 $U(k,t)=\mathcal{F}[u(x,t)]={\int }_{-\infty }^{+\infty }u(x,t)e^{-\mathrm{i}kx}dx$ ，运用用含参变量的积分及傅里叶变换的微分性质

则定解问题变为关于 $t$ 的常微分方程及初值条件
$$\{\begin{array}{l}{U}^{\prime \prime }+k^2{a}^{2}U=0\\ U(0)=\Phi (k),U^{\prime }(0)=\Psi (k)\end{array}$$
其中 $\Phi (k)=\mathcal{F}[\varphi (x)],\Psi (k)=\mathcal{F}[\psi (x)]$ 分别是 $\varphi (x),\psi (x)$ 关于 $x$ 的傅里叶变换。其解为
$$U(k,t)=\Phi (k)\cos kat+\frac{1}{ka}\Psi (k)\sin kat$$

最后，对 $U(k,t)$ 做傅里叶逆变换，用延迟性质和积分性质，结果是
$$u(x,t)=\frac{1}{2}[\varphi (x+at)+\varphi (x-at)]+\frac{1}{2a}{\int }_{x-at}^{x+at}\psi (\xi )d\xi$$
这个公式正是达朗贝尔(d’Alembert)公式。

求无限长杆的有源热传导问题
$$\{\begin{array}{l}{u}_t-a^2{u}_{xx}=f(x,t)\\ u{|}_{t=0}=\varphi (x)\end{array}$$
解：做傅里叶变换，定解问题变为
$$\{\begin{array}{l}{U}^{\prime }+k^2{a}^{2}U=F(k,t)\\ U(0)=\Phi (k)\end{array}$$
其中 $U(k,t)=\mathcal{F}[u(x,t)],F(k,t)=\mathcal{F}[f(x,t)],\Phi (k)=\mathcal{F}[\varphi (x)]$ 分别是 $u(x,t),f(x,t),\varphi (x)$ 关于 $x$ 的傅里叶变换。这个常微分方程初值问题的解为
$$U(k,t)=\Phi (k)e^{-k^2{a}^{2}t}+{\int }_0^{t}F(k,\tau )e^{-k^2{a}^2(t-\tau )}d\tau$$

最后，对 $U(k,t)$ 做傅里叶逆变换，用卷积定理，结果是
$$u(x,t)={\int }_{-\infty }^{+\infty }\varphi (\xi )\frac{1}{2a\sqrt{\pi t}}\exp [-\frac{(x-\xi {)}^2}{4a^{2}t}]d\xi +{\int }_0^t{\int }_{-\infty }^{+\infty }\frac{f(\xi ,\tau )}{2a\sqrt{\pi (t-\tau )}}\exp [-\frac{(x-\xi {)}^2}{4a^2(t-\tau )}]d\xi d\tau$$

傅里叶正弦变换或余弦变换：如果 $f(x)$ 定义在半无界区间 $[0,+\infty )$ 上，满足狄利克雷(Dirichlet)条件¹且绝对可积，则有傅里叶正弦变换
$$\begin{gathered} F(k)={\int }_0^{+\infty }f(x)\sin kx\text{d}x \\ f(x)=\frac{1}{2\pi }{\int }_0^{+\infty }F(k)\sin kx\text{d}k \end{gathered}$$
或余弦变换
$$\begin{gathered} G(k)={\int }_0^{+\infty }g(x)\cos kx\text{d}x \\ g(x)=\frac{1}{2\pi }{\int }_0^{+\infty }G(k)\cos kx\text{d}k \end{gathered}$$
对于半无界空间，存在自然边界条件
$$\underset{x\to \infty }{\lim }f(x)=0,\underset{x\to \infty }{\lim }{f}^{\prime }(x)=0$$
可以采用正弦变换或余弦变换，对于正弦变换
导数的正弦变换为
$$\begin{array}{rl}& {\int }_0^{+\infty }{f}^{\prime }(x)\sin kx\text{d}x\\ =& f(x)\sin kx{|}_0^{+\infty }-k{\int }_0^{+\infty }f(x)\cos kx\text{d}x\\ =& -k{\int }_0^{+\infty }f(x)\cos kx\text{d}x\end{array}$$
二阶导正弦变换为
$$\begin{array}{rl}& {\int }_0^{+\infty }{f}^{\prime \prime }(x)\sin kx\text{d}x\\ =& -k{\int }_0^{+\infty }{f}^{\prime }(x)\cos kx\text{d}x\\ =& -k[f(x)\cos kx{|}_0^{+\infty }+k{\int }_0^{+\infty }f(x)\sin kx\text{d}x]\\ =& kf(0)-k^{2}F(k)\end{array}$$

由此可见，对于二阶偏微分方程的定解问题，只有在半无界空间的 $x=0$ 端给出第一类边界条件时，才可以采用正弦变换。

同样对于余弦变换，也有
$$\begin{gathered} {\int }_0^{+\infty }{g}^{\prime }(x)\cos kx\text{d}x=-g(0)+k{\int }_0^{+\infty }g(x)\sin kx\text{d}x \\ {\int }_0^{+\infty }{g}^{\prime \prime }(x)\cos kx\text{d}x=-g^{\prime }(0)-k^{2}G(k) \end{gathered}$$
由此可见，对于二阶偏微分方程的定解问题，只有在半无界空间的 $x=0$ 端给出第二类边界条件时，才可以采用余弦变换。

求半无界杆的热传导问题
$$\{\begin{array}{ll}{u}_t-a^2{u}_{xx}=0& (x>0)\\ u{|}_{t=0}=0& \\ u{|}_{x=0}=u_0& \end{array}$$
解：采用傅里叶正弦变换，定解问题变为
$$\{\begin{array}{l}{U}^{\prime }+k^2{a}^{2}U=k{a}^2{u}_0\\ U(0)=0\end{array}$$
其中 $U(k,t)$ 是 $u(x,t)$ 关于 $x$ 的傅里叶正弦变换。这个常微分方程初值问题的解为
$$U(k,t)=\frac{u_0}{k}(1-e^{-k^2{a}^{2}t})$$

最后，对 $U(k,t)$ 做傅里叶逆变换，结果是
$$u(x,t)=\frac{2u_0}{\pi }{\int }_0^{+\infty }\frac{1}{k}(1-e^{-k^2{a}^{2}t})\sin kxdk$$
通常记误差函数 (error function)
$$\mathrm{e}\mathrm{r}\mathrm{f}(x)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-s^2}ds$$
和余误差函数 (error function complement)
$$\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}(x)=1-\mathrm{e}\mathrm{r}\mathrm{f}(x)=\frac{2}{\sqrt{\pi }}{\int }_x^{\infty }{e}^{-s^2}ds$$
故 $u(x,t)$ 可进一步变换为²
$$u(x,t)=\frac{2u_0}{\pi }[\frac{\pi }{2}-\frac{\pi }{2}\mathrm{e}\mathrm{r}\mathrm{f}(\frac{x}{2a\sqrt{t}})]=u_0\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}(\frac{x}{2a\sqrt{t}})$$

求三维无界空间中的波动问题
$$\{\begin{array}{l}{u}_{tt}-a^2\Delta u=0\\ u{|}_{t=0}=\varphi (x,y,z),\frac{\partial u}{\partial t}{|}_{t=0}=\psi (x,y,z)\end{array}$$
解：作三重傅里叶变换，记 $\mathbf{r}=(x,y,z),\mathbf{k}=(k_1,k_2,k_3)$，定解问题变为
$$\{\begin{array}{l}{U}^{\prime \prime }+{\mathbf{k}}^2{a}^{2}U=0\\ U(0)=\Phi (\mathbf{k}),U^{\prime }(0)=\Psi (\mathbf{k})\end{array}$$
其中 $U(\mathbf{k},t),\Phi (\mathbf{k}),\Psi (\mathbf{k})$ 分别是 $u(\mathbf{r},t),\varphi (\mathbf{r}),\psi (\mathbf{r})$ 关于 $\mathbf{r}$ 的三维傅里叶变换。这个常微分方程初值问题的解为
$$U(\mathbf{k},t)=\Phi (\mathbf{k})\cos kat+\Psi (\mathbf{k})\frac{\sin kat}{ka}$$

其中 $k=|\mathbf{k}|=\sqrt{k_1^2+k_2^2+k_3^2}$ ，再进行傅里叶逆变换
$$\begin{array}{rl}u(\mathbf{r},t)& =\frac{1}{(2\pi {)}^3}\underset{-\infty }{\overset{+\infty }{\iiint }}[\Phi (\mathbf{k})\cos kat+\Psi (\mathbf{k})\frac{\sin kat}{ka}]e^{\mathrm{i}\mathbf{k}\cdot \mathbf{r}}d\mathbf{k}\\ & =\frac{1}{4\pi a}\frac{\partial }{\partial t}\underset{S_{at}^{\mathbf{r}}}{\iint }\frac{\varphi (\mathbf{r})}{at}dS+\frac{1}{4\pi a}\frac{\partial }{\partial t}\underset{S_{at}^{\mathbf{r}}}{\iint }\frac{\psi (\mathbf{r})}{at}dS\end{array}$$
上式称为泊松公式。式中 $S_{at}^{\mathbf{r}}$ 表示以 $\mathbf{r}$ 为圆心，以 $at$ 为半径的球面，$dS$ 表示 $S_{at}^{\mathbf{r}}$ 的面积元。

拉普拉斯变换法

拉普拉斯变换法适合求解初值问题，不管方程和边界条件是否为齐次的。

Laplace变换：设函数$f(t)$ 在 $t⩾0$ 时有定义，且积分 ${\int }_0^{+\infty }f(t)e^{-st}dt$ 收敛，则此积分所确定的函数
$$F(s)={\int }_0^{+\infty }f(t)e^{-st}\text{d}t\text{\hspace{1em}(2.1)}$$
称为函数 $f(t)$ 的 Laplace 变换，记为 $F(s)=\mathcal{L}[f(t)]$，函数 $F(s)$ 也可称为 $f(t)$的象函数。
Laplace逆变换：令 $s=\beta +i\omega$ ，则有
$$f(t)=\frac{1}{2\pi i}{\int }_{\beta -i\omega }^{\beta +i\omega }F(s)e^{st}\text{d}s(t>0)$$
称为 Laplace 逆变换，记为 $f(t)={\mathcal{L}}^{-1}[F(s)]$ 。在Laplace 变换中，只要求$f(t)$在 $[0,+\infty )$ 内有定义即可。为了研究方便，以后总假定在$(-\infty ,0)$ 内，$f(t)\equiv 0$
还可用留数就算拉普拉斯逆变换：设在复平面内只有有限个孤立奇点 $s_1,s_2,\cdots ,s_n$ ，实数 $\beta$使这些奇点全在半平面 $\text{Re}(s)<\beta$ 内，且 $\underset{s\to \infty }{\lim }F(s)=0$ ，则有
$$f(t)=\sum _{k=1}^n\text{Res}[F(s)e^{st},s_k](t>0)$$

求半无界杆的热传导问题
$$\{\begin{array}{ll}{u}_t-a^2{u}_{xx}=0& (x>0)\\ u{|}_{t=0}=0& (x>0)\\ u{|}_{x=0}=u_0& \end{array}$$
解：对方程和边界条件关于 $t$ 进行拉普拉斯变换，采用微分性质，变换结果为
$$\{\begin{array}{l}sU-a^2{U}^{\prime \prime }=0\\ U(0)=\frac{1}{s}{u}_0\end{array}$$
其中 $U(s,x)$ 是 $u(x,t)$ 关于 $t$ 的傅里叶正弦变换。这个常微分方程通解为
$$U(s,x)=A\exp (-\frac{\sqrt{sx}}{a})+B\exp (\frac{\sqrt{sx}}{a})$$
考虑到自然边界条件 $\underset{x\to \infty }{\lim }U$应为有限值，带入初值条件可求得
$$U(s,x)=\frac{1}{s}{u}_0\exp (-\frac{\sqrt{sx}}{a})$$
最后，对 $U(s,x)$ 进行拉普拉斯逆变换[^L1]
$$u(x,t)=u_0\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}(\frac{x}{2a\sqrt{t}})$$

求长 $l$ 均匀细杆的热传导问题
$$\{\begin{array}{ll}{u}_t-a^2{u}_{xx}=0& (0<x<l)\\ u{|}_{t=0}=0& (0<x<l)\\ u{|}_{x=0}=u_0,\frac{\partial u}{\partial x}{|}_{x=l}=0& \end{array}$$
解：对方程和边界条件关于 $t$ 进行拉普拉斯变换，采用微分性质，变换结果为
$$\{\begin{array}{l}sU-a^2{U}^{\prime \prime }=0\\ U(0)=\frac{1}{s}{u}_0,U^{\prime }(l)=0\end{array}$$
其中 $U(s,x)$ 是 $u(x,t)$ 关于 $t$ 的傅里叶正弦变换。这个二阶常微分方程的解为
$$U(s,x)=\frac{1}{s}{u}_0\frac{\cosh \frac{(l-x)\sqrt{s}}{a}}{\cosh \frac{l\sqrt{s}}{a}}$$
最后，利用留数定理对 $U(s,x)$ 进行拉普拉斯逆变换
$$u(x,t)=u_0-\frac{\pi u_0}{4}\sum _{n=0}^{\infty }\frac{1}{2n+1}\sin \left(\frac{2n+1}{2l}\pi x\right)\exp \left[-{\left(\frac{2n+1}{2l}\pi \right)}^2{a}^{2}t\right]$$

基本解和格林函数

格林函数，又称点源影响函数，代表一个点源在一定的边界条件和（或）初始条件下所产生的场。均匀分布的函数可看做点源的叠加，该想法来源于静电场叠加原理。实际上，这种做法只不过是利用了偏微分方程的积分叠加原理。

泊松方程的基本解

引例：先举一个静电场的例子，设无界空间中电荷密度为 $\rho (\mathbf{r})$ ，这样在坐标 ${\mathbf{r}}_0=(x_0,y_0,z_0)$ 的体积元 $d{V}_0$ 内的电荷量为 $\rho ({\mathbf{r}}_0)d{V}_0$ ，它在空间点 $\mathbf{r}=(x,y,z)$ 产生的电势为
$$\frac{1}{4\pi {\epsilon }_0}\frac{\rho ({\mathbf{r}}_0)}{|\mathbf{r}-{\mathbf{r}}_0|}$$
根据电势叠加原理，可叠加求得任意密度分布引起的总电势分布
$$\phi (\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}\iiint \frac{\rho ({\mathbf{r}}_0)}{|\mathbf{r}-{\mathbf{r}}_0|}d{V}_0$$
泊松方程的基本解：对于无界空间的泊松方程
$$\Delta u=f(\mathbf{r})\text{\hspace{1em}(1.1)}$$
在物理上可看做电荷密度分布 $-{\epsilon }_{0}f(\mathbf{r})$ 在无界空间的电势方程。为了研究点源产生的场， $\delta$ 函数恰是一个表示点源密度的函数，由 $\delta$ 函数的性质知
$$\iiint f({\mathbf{r}}_0)\delta (\mathbf{r}-{\mathbf{r}}_0)\mathrm{d}{V}_0=f(\mathbf{r})$$
这说明一般源 $f(\mathbf{r})$ 可看成 ${\mathbf{r}}_0$ 点的点源 $f({\mathbf{r}}_0)\delta (\mathbf{r}-{\mathbf{r}}_0)$ 的积分叠加，由第一章积分叠加原理知道，只需求出方程
$$\Delta G(\mathbf{r},{\mathbf{r}}_0)=\delta (\mathbf{r}-{\mathbf{r}}_0)\text{\hspace{1em}(1.2)}$$
的解 $G({\mathbf{r},\mathbf{r}}_0)$ ，便可得无界空间泊松方程的解
$$u(\mathbf{r})=\iiint G({\mathbf{r},\mathbf{r}}_0)f({\mathbf{r}}_0)\mathrm{d}{V}_0\text{\hspace{1em}(1.3)}$$
其中 $G({\mathbf{r},\mathbf{r}}_0)$ 称为格林函数，又称点源影响函数。
由于是在无界空间，不妨先做平移变换，求方程（拉普拉斯算符平移不变性）
$$\Delta U(\mathbf{r})=\delta (\mathbf{r})\text{\hspace{1em}(1.4)}$$
的解 $U(\mathbf{r})$，称为基本解，代表置于原点的点源引起的场。则
$$G(\mathbf{r},{\mathbf{r}}_0)=U(\mathbf{r}-{\mathbf{r}}_0)\text{\hspace{1em}(1.5)}$$
进而有
$$u(\mathbf{r})=\iiint U(\mathbf{r}-{\mathbf{r}}_0)f({\mathbf{r}}_0)\mathrm{d}{V}_0=U(\mathbf{r})\ast f(\mathbf{r})\text{\hspace{1em}(1.6)}$$
基本解的求法：在物理上， 基本解 $U(\mathbf{r})$ 描述了位于原点电荷量为 $-{\epsilon }_0$ 的电荷在无界空间 $\mathbf{r}$ 处的电势。这里基本解没有定解条件限制，因此不是惟一的，通常根据问题的物理意义和数学的需要选定其中一个。
下面介绍数学上的一种求解方法。将方程用球坐标表示，当 $r\ne 0$ 时，由于函数关于 $r$ 对称，所以方程化为
$$\frac{1}{r^2}\frac{d}{dr}(r^2\frac{dU}{dr})=0$$
其解为
$$U=-\frac{c_1}{r}+c_2$$
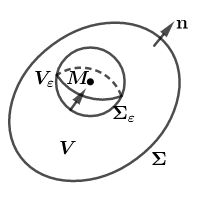
一般令无穷远处 $U=0$，则 $c_2=0$ 。为了求出 $c_1$ ，将方程包含原点的区域（不妨取以 $ϵ$ 为半径的球 $V_{ϵ}$）进行体积分，利用 $\delta$ 函数的性质
$$\underset{V_{ϵ}}{\iiint }\Delta UdV=1$$
利用格林公式，将上述体积分化为面积分
$$\underset{V_{ϵ}}{\iiint }\Delta UdV=\underset{{\Sigma }_{ϵ}}{\iint }\frac{\partial U}{\partial r}dS={\int }_0^{2\pi }{\int }_0^{\pi }{r}^2\sin \theta d\theta d\varphi =4\pi c_1$$
于是 $c_1=\frac{1}{4\pi }$ ，从而三维泊松方程基本解
$$U(\mathbf{r})=-\frac{1}{4\pi r}\text{\hspace{1em}(1.7)}$$
类似的，用平面极坐标可求得二维泊松方程的基本解
$$U(\mathbf{r})=-\frac{1}{2\pi }\ln \frac{1}{r}=\frac{1}{2\pi }\ln r\text{\hspace{1em}(1.8)}$$

泊松方程的格林函数

泊松方程的边值问题：泊松方程第一、第二、第三类边值问题可统一表示为
$$\{\begin{array}{ll}\Delta u=f(\mathbf{r})& (\mathbf{r}\in V)\\ (\alpha \frac{\partial u}{\partial n}+\beta u){|}_{\Sigma }=\varphi (\mathbf{r})& (\mathbf{r}\in \Sigma )\end{array}\text{\hspace{1em}(2.1)}$$
若 $\alpha =0,\beta \ne 0$ 为第一类边值问题；若 $\alpha \ne 0,\beta =0$ 为第二类边值问题；若 $\alpha \ne 0,\beta \ne 0$ 为第三类边值问题。由上节知道格林函数满足方程
$$\Delta G(\mathbf{r},{\mathbf{r}}_0)=\delta (\mathbf{r}-{\mathbf{r}}_0)\text{\hspace{1em}(2.2)}$$
从物理上看，格林函数就是位于 ${\mathbf{r}}_0$点电荷量为 $-{\epsilon }_0$ 的电荷在区域 $V$ 内 $\mathbf{r}$ 点产生的电势。
现在，我们开始使用格林公式，叠加出泊松方程边值问题的解。为此，我们将 (2.1) 中泊松方程和方程 (2.2) 分别乘上 $G(\mathbf{r},{\mathbf{r}}_0)$ 和 $u(\mathbf{r})$ ，相减，然后在区域 $V$ 内积分，得到
$$\underset{V}{\iiint }(G\Delta u-u\Delta G)dV=\underset{V}{\iiint }GfdV-\underset{V}{\iiint }u(\mathbf{r})\delta (\mathbf{r}-{\mathbf{r}}_0)dV$$
根据格林公式，可以将上式左端化为面积分
$$\underset{V}{\iiint }(G\Delta u-u\Delta G)dV=\underset{\Sigma }{\iint }(G\frac{\partial u}{\partial n}-u\frac{\partial G}{\partial n})\mathrm{d}S$$
右端第二项根据 $\delta$ 函数的性质可以得到
$$\underset{V}{\iiint }u(\mathbf{r})\delta (\mathbf{r}-{\mathbf{r}}_0)dV=u({\mathbf{r}}_0)$$
于是，可以得到
$$u({\mathbf{r}}_0)=\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f(\mathbf{r})dV-\underset{\Sigma }{\iint }[G(\mathbf{r},{\mathbf{r}}_0)\frac{\partial u(\mathbf{r})}{\partial n}-u(\mathbf{r})\frac{\partial G(\mathbf{r},{\mathbf{r}}_0)}{\partial n}]\mathrm{d}S\text{\hspace{1em}(2.3)}$$
上式称为泊松方程的基本积分公式。
需要注意的是，$G(\mathbf{r},{\mathbf{r}}_0)$ 在 $\mathbf{r}={\mathbf{r}}_0$ 是不连续的，格林公式并不适用。严格的证明是，先在区域 $V$ 内奇点 ${\mathbf{r}}_0$ 处挖去半径为 $\epsilon$ 的球形区域 $V_{\epsilon }$ ，应用格林公式，再令 $\epsilon \to 0$ 取极限求得。今后类似使用时将不再加以说明。

基本积分公式将泊松方程的解 $u$ 用体积分和边界上的面积分表示了出来。对于面积分，$u$ 的边界条件是已知的，如果我们对 $G(\mathbf{r},{\mathbf{r}}_0)$ 提出适当的边界条件，从而获得格林函数确切的解，就可以将 $u$ 确切的表示出来。

(1) 如果泊松方程满足第一类边界条件
$$u{|}_{\Sigma }=\varphi (\mathbf{r})(\mathbf{r}\in \Sigma )$$
同时要求 $G(\mathbf{r},{\mathbf{r}}_0)$ 满足第一类齐次边界条件，即解决边值问题
$$\{\begin{array}{l}\Delta G(\mathbf{r},{\mathbf{r}}_0)=\delta (\mathbf{r}-{\mathbf{r}}_0)\\ G{|}_{\Sigma }=0\end{array}$$
则积分公式 (2.3) 含 $\frac{\partial u}{\partial n}$ 的一项为零，所以不需要知道$\frac{\partial u}{\partial n}$ 在边界上的值，上述边值问题的解称为泊松方程第一边值问题的格林函数。在物理上，可看做边界接地条件下，区域 $V$ 内 ${\mathbf{r}}_0$ 点（点源）电荷为 $-{\epsilon }_0$ 的点源在 $V$ 内 $\mathbf{r}$ 点的电势。基本积分公式
$$u({\mathbf{r}}_0)=\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f(\mathbf{r})dV+\underset{\Sigma }{\iint }\varphi (\mathbf{r})\frac{\partial G(\mathbf{r},{\mathbf{r}}_0)}{\partial n}\mathrm{d}S$$
(2) 如果泊松方程满足第三类边界条件
$$(\alpha \frac{\partial u}{\partial n}+\beta u){|}_{\Sigma }=\varphi (\mathbf{r})(\mathbf{r}\in \Sigma )$$
令 $G(\mathbf{r},{\mathbf{r}}_0)$ 满足第三类齐次边界条件，即解决边界问题
$$\{\begin{array}{l}\Delta G(\mathbf{r},{\mathbf{r}}_0)=\delta (\mathbf{r}-{\mathbf{r}}_0)\\ (\alpha \frac{\partial G}{\partial n}+\beta G){|}_{\Sigma }=0\end{array}$$
分别用 $G,u$ 或 $\frac{\partial G}{\partial n},\frac{\partial u}{\partial n}$ 交叉相乘上述两方程，并相减，可以得到
$$(G\frac{\partial u}{\partial n}-u\frac{\partial G}{\partial n}){|}_{\Sigma }=\frac{1}{\alpha }G\varphi =-\frac{1}{\beta }\frac{\partial G}{\partial n}\varphi$$
上述边值问题的解称为泊松方程第三边值问题的格林函数，此时
$$\begin{array}{rl}u({\mathbf{r}}_0)& =\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f(\mathbf{r})dV-\frac{1}{\alpha }\underset{\Sigma }{\iint }\varphi (\mathbf{r})G(\mathbf{r},{\mathbf{r}}_0)\mathrm{d}S\\ & =\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f(\mathbf{r})dV+\frac{1}{\beta }\underset{\Sigma }{\iint }\varphi (\mathbf{r})\frac{\partial G(\mathbf{r},{\mathbf{r}}_0)}{\partial n}\mathrm{d}S\end{array}$$
(3) 至于第二类边界条件
$$\frac{\partial u}{\partial n}{|}_{\Sigma }=\varphi (\mathbf{r})(\mathbf{r}\in \Sigma )$$
似乎可以按照上面的方法，即解决边值问题
$$\{\begin{array}{l}\Delta G(\mathbf{r},{\mathbf{r}}_0)=\delta (\mathbf{r}-{\mathbf{r}}_0)\\ \frac{\partial G}{\partial n}{|}_{\Sigma }=0\end{array}$$
在格林公式中，令 $u(\mathbf{r})=1,v(\mathbf{r})=G(\mathbf{r},{\mathbf{r}}_0)$ ，则有
$$\underset{V}{\iiint }\Delta G(\mathbf{r},{\mathbf{r}}_0)\mathrm{d}V=\underset{\Sigma }{\iint }\nabla G(\mathbf{r},{\mathbf{r}}_0)\cdot \mathrm{d}\mathbf{S}=\underset{\Sigma }{\iint }\frac{\partial G(\mathbf{r},{\mathbf{r}}_0)}{\partial n}\mathrm{d}S$$
对边值问题中方程进行积分，根据 $\delta$ 函数的性质又得到
$$\underset{V}{\iiint }\Delta G(\mathbf{r},{\mathbf{r}}_0)\mathrm{d}V=1$$
于是格林函数在边界上的积分必须满足
$$\underset{\Sigma }{\iint }\frac{\partial G(\mathbf{r},{\mathbf{r}}_0)}{\partial n}\mathrm{d}S=1\ne 0$$
这显然和上述边值问题中边界条件是矛盾的，第二类齐次边界问题一定无解。此时，需要引进广义的格林函数
$$\{\begin{array}{l}\Delta G(\mathbf{r},{\mathbf{r}}_0)=\delta (\mathbf{r}-{\mathbf{r}}_0)-\frac{1}{v}\\ \frac{\partial G}{\partial n}{|}_{\Sigma }=0\end{array}$$
其中 $v$ 是区域 $V$ 的体积，并且当且仅当
$$\underset{V}{\iiint }f(\mathbf{r})dV=-\underset{\Sigma }{\iint }\varphi (\mathbf{r})\mathrm{d}S$$
相应边值问题解的积分公式为
$$u({\mathbf{r}}_0)=\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f(\mathbf{r})dV-\underset{\Sigma }{\iint }\varphi (\mathbf{r})G(\mathbf{r},{\mathbf{r}}_0)\mathrm{d}S$$
格林函数的对称性：上述积分公式，似乎没有明确的物理意义。接下来我们先讨论格林函数的一个重要性质
$$G({\mathbf{r}}_1,{\mathbf{r}}_2)=G({\mathbf{r}}_2,{\mathbf{r}}_1)\text{\hspace{1em}(2.4)}$$
引入两个格林函数 $G(\mathbf{r},{\mathbf{r}}_1),G(\mathbf{r},{\mathbf{r}}_2)$，以第一类边界问题为例
$$\{\begin{array}{l}\Delta G(\mathbf{r},{\mathbf{r}}_1)=\delta (\mathbf{r}-{\mathbf{r}}_1)\\ G(\mathbf{r},{\mathbf{r}}_1){|}_{\Sigma }=0\end{array},\{\begin{array}{l}\Delta G(\mathbf{r},{\mathbf{r}}_2)=\delta (\mathbf{r}-{\mathbf{r}}_2)\\ G(\mathbf{r},{\mathbf{r}}_2){|}_{\Sigma }=0\end{array}(\mathbf{r},{\mathbf{r}}_1,{\mathbf{r}}_2\in V)$$
利用 $\delta$ 函数的性质和格林公式，上述方程可以得到
$$\begin{array}{rl}& G({\mathbf{r}}_1,{\mathbf{r}}_2)-G({\mathbf{r}}_2,{\mathbf{r}}_1)\\ =& \underset{V}{\iiint }[G(\mathbf{r},{\mathbf{r}}_2)\delta (\mathbf{r}-{\mathbf{r}}_1)-G(\mathbf{r},{\mathbf{r}}_1)\delta (\mathbf{r}-{\mathbf{r}}_2)]\mathrm{d}V\\ =& \underset{V}{\iiint }[G(\mathbf{r},{\mathbf{r}}_2)\Delta G(\mathbf{r},{\mathbf{r}}_1)-G(\mathbf{r},{\mathbf{r}}_1)\Delta G(\mathbf{r},{\mathbf{r}}_2)]\mathrm{d}V\\ =& \underset{\Sigma }{\iint }[G(\mathbf{r},{\mathbf{r}}_2)\nabla G(\mathbf{r},{\mathbf{r}}_1)-G(\mathbf{r},{\mathbf{r}}_1)\nabla G(\mathbf{r},{\mathbf{r}}_2)]\cdot \mathrm{d}\mathbf{S}\end{array}$$
带入边界条件，可得出面积分等于零，于是
$$G({\mathbf{r}}_1,{\mathbf{r}}_2)=G({\mathbf{r}}_2,{\mathbf{r}}_1)$$
对于第二类、第三类边界条件也可以得到同样的结果。

综上所述：对于泊松方程积分公式中的 $\mathbf{r}$ 和 ${\mathbf{r}}_0$ 互换下位置，并利用格林函数的对称性可得
第一边值问题解的积分表达式为
$$u(\mathbf{r})=\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f({\mathbf{r}}_0)\mathrm{d}{V}_0+\underset{\Sigma }{\iint }\varphi ({\mathbf{r}}_0)\frac{\partial G(\mathbf{r},{\mathbf{r}}_0)}{\partial n}\mathrm{d}{S}_0$$
第二边值问题解的积分表达式为
$$u(\mathbf{r})=\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f({\mathbf{r}}_0)\mathrm{d}{V}_0-\underset{\Sigma }{\iint }\varphi ({\mathbf{r}}_0)G(\mathbf{r},{\mathbf{r}}_0)\mathrm{d}{S}_0$$
第三边值问题解的积分表达式为
$$\begin{array}{rl}u(\mathbf{r})& =\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f({\mathbf{r}}_0)\mathrm{d}{V}_0-\frac{1}{\alpha }\underset{\Sigma }{\iint }\varphi ({\mathbf{r}}_0)G(\mathbf{r},{\mathbf{r}}_0)\mathrm{d}{S}_0\\ & =\underset{V}{\iiint }G(\mathbf{r},{\mathbf{r}}_0)f({\mathbf{r}}_0)d{V}_0+\frac{1}{\beta }\underset{\Sigma }{\iint }\varphi ({\mathbf{r}}_0)\frac{\partial G(\mathbf{r},{\mathbf{r}}_0)}{\partial n}\mathrm{d}{S}_0\end{array}$$
此时，积分公式有明确的物理意义，右边第一个积分表示在区域 $V$ 内分布的点源在 $\mathbf{r}$ 处产生的场的总和，而第二项则代表边界面上感生场对 $\mathbf{r}$ 处场的影响的总和。

用镜像法求格林函数

泊松方程第一、第三类边值问题对应的格林函数满足
$$\{\begin{array}{ll}\Delta G=\delta (\mathbf{r}-{\mathbf{r}}_0)& (\mathbf{r}\in V)\\ (\alpha \frac{\partial G}{\partial n}+\beta G){|}_{\Sigma }=0& (\mathbf{r}\in \Sigma )\end{array}\text{\hspace{1em}(3.1)}$$
下面介绍格林函数的两种解法

• 第一种是按相应齐次问题及边界条件的本征函数展开，用分离变量法求得，但这样得到的解往往是无穷级数。
• 格林函数的物理意义启发我们，对于某些特殊区域，格林函数可以通过镜像法求得，可以取得有限形式的解。

镜像法：例如泊松方程第一边值问题的格林函数
$$\{\begin{array}{ll}\Delta G=\delta (\mathbf{r}-{\mathbf{r}}_0)& (\mathbf{r}\in V)\\ G{|}_{\Sigma }=0& (\mathbf{r}\in \Sigma )\end{array}$$
在物理上可理解为，一接地导体 $V$ 内 ${\mathbf{r}}_0$ 点电荷量为 $-{\epsilon }_0$ 的点电荷在 $V$ 内 $\mathbf{r}$ 点的电势。
由叠加原理，通常将格林函数 $G$ 分成两部分
$$G(\mathbf{r},{\mathbf{r}}_0)=G_0(\mathbf{r},{\mathbf{r}}_0)+G_1(\mathbf{r},{\mathbf{r}}_0)$$
其中 $U$ 满足
$$\Delta G_0=\delta (\mathbf{r}-{\mathbf{r}}_0)$$
是 ${\mathbf{r}}_0$ 点的点电荷产生的场，$G_1$ 满足
$$\{\begin{array}{l}\Delta G_1=0\\ G_1{|}_{\Sigma }=-G_0{|}_{\Sigma }\end{array}$$
是导体内 ${\mathbf{r}}_0$ 点的点电荷在边界上的感应电荷产生的场。
利用第一节中的基本解可知，在三维情形下
$$G_0(\mathbf{r},{\mathbf{r}}_0)=-\frac{1}{4\pi }\frac{1}{|\mathbf{r}-{\mathbf{r}}_0|}\text{\hspace{1em}(3.2)}$$
类似的，二维情形下
$$G_0(\mathbf{r},{\mathbf{r}}_0)=-\frac{1}{2\pi }\ln \frac{1}{|\mathbf{r}-{\mathbf{r}}_0|}=\frac{1}{2\pi }\ln |\mathbf{r}-{\mathbf{r}}_0|\text{\hspace{1em}(3.3)}$$
由于区域 $V$ 外的电源在 $V$ 内产生的场满足拉普拉斯方程，镜像法的中心思想是把边界上的感生电荷用一个等价的点电荷（像电荷）代替，困难在于 $V$ 内点电荷的电场在边界上必须和像电荷的电场相抵消，只有在某些特殊区域（例如，球形，半无界空间，等等）才能实现。

求球内泊松方程第一边值问题格林函数：
$$\{\begin{array}{ll}\Delta G=\delta (\mathbf{r}-{\mathbf{r}}_0)& (0<r,r_0<a)\\ G{|}_{r=a}=0& \end{array}$$
(1) 像电荷如果存在的话，一定在球外。这是由于感应电荷的电势在球内是处处连续的，在球内的任何电荷都不能产生同样的效果。
(2) 考虑到对称性，这个像电荷一定存在于真实电荷所在半径的延长线上。
记球内电荷位于点 $Q_0({\mathbf{r}}_0)$ ，像电荷位于点 $Q_1({\mathbf{r}}_1)$ 电量为 $q$ ，如图

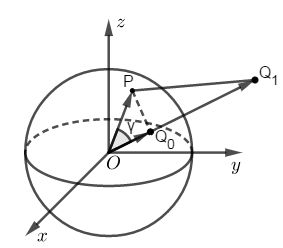
在球内任取一点 $P(\mathbf{r})$ ，由叠加原理知道，总电势是球内电荷产生的电势和像电荷产生的电势叠加
$$G=-\frac{1}{4\pi }\frac{1}{|\mathbf{r}-{\mathbf{r}}_0|}+\frac{q}{4\pi {\epsilon }_0}\frac{1}{|\mathbf{r}-{\mathbf{r}}_1|}$$
引入球坐标系（原点在球心），由于 ${\mathbf{r}}_0,{\mathbf{r}}_1$ 共线，设 ${\mathbf{r}}_1=\lambda {\mathbf{r}}_0$ 则
$$\begin{gathered} |\mathbf{r}-{\mathbf{r}}_0|=P{Q}_0=\sqrt{r^2-2r{r}_0\cos \gamma +r_0^2} \\ |\mathbf{r}-{\mathbf{r}}_1|=P{Q}_1=\sqrt{r^2-2\lambda r{r}_0\cos \gamma +{\lambda }^2{r}_0^2} \end{gathered}$$
其中 $\gamma$ 是矢径 $\mathbf{r}$ 和 ${\mathbf{r}}_0$ $({\mathbf{r}}_1)$ 之间的夹角
$$\cos \gamma =\cos \theta \cos {\theta }_0+$$