算法设计与分析:蛮力法
算法分析与设计实验报告
第 四 次实验
姓名 裴朵朵 学号 5001170016 班级 计科一班
时间 2019.10.31 地点
实验名称 暴力法的使用
实验目的 1、理解暴力法的工作原理、过程技巧,掌握常用的暴力法案例(幂级数、全排列等)
2、应用暴力法求解日常生活中问题
实验原理 1.求数组a中大小相差最小的两个元素的差
2.给定一个整数数组A=(a0,a1,a2…an-1),若i
3.对于给定的正整数n(n>1),采用蛮力法求1!+2!+…n!,并改进该算法提高效率
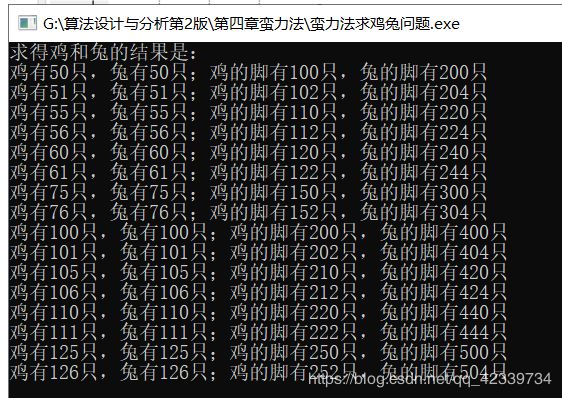
4.有一群鸡和一群兔,它们的只数相同,它们的脚数都是三位数,且这两个三位数的各位数字只能是0,1,2,3,4,5.设计一个算法用蛮力法求鸡和兔各有有多少只,他它们的脚数各是多少。
5.有一个三位数,个位数字比百位数字大,百位数字又比十位数字大,并且各位数 字之和等于各位数字相乘之积,设计一个算法用穷举法求此三位数
6.某年级的同学集体去公园划船,如果每只船坐10人,那么多出两个座位;如果每只船多坐两人,那么可少租1只船,设计一个算法用蛮力法求该年级的最多人数
7. 若一个合数的质因数分解式逐位相加之和等于其本身逐位相加之和,则称这个数为Smith数。给定一个正整数N,求大于N的最小Smith数
8.求解涂棋盘问题。小易有一块n*n的棋盘,棋盘的每一个格子都为黑色或者白色,小易现在要用他最喜欢的红色去图画棋盘。小易会找出棋盘的某一列中拥有相同颜色的最大区域去涂画,帮助小易算算他会图画多少个棋格
9.对于给定的正整数n(n>=1),求1~n的所有全排列
10.对于给定的正整数n(n>=1),求1n构成的集合的幂集,即由1n的集合中所有子集构成的集合,包括全集和空集。
实验步骤 1.先将数组a中的元素按递增顺序排列,然后求相邻两个元素的差,最小的差值即为所求
2.此题采用蛮力法性能较差,思路是:依次比较每个元素与其后面元素的大小,若该元素的值大于其后面的元素,则逆序数加1,直到比较结束
3.n!可用for循环求得,同样的,n-1的阶乘也可用for循环求出,所以本题可以用循环嵌套求出
4.设鸡脚数是y=abc,兔脚数是z=def,确定每个数字的取值范围,鸡只数是y/2,兔只数是z/4,当两个值相等时即为所求
5.设此三位数是x=abc,a
6.每条船坐10人,有x个学生,y只船,则10y-2=x;m每条船多坐2人,即12人,要求求出最大的人数,则此时少租1只船,船上没有空余座位,此时12(y-1)=x;
7.采用蛮力法求出用户输入的n的各个位数的和sum,求n的所有质因数的和count,若sum==count,则输出,否则,n++,直到求出最小Smith数
8.统计每一列相邻相同颜色的棋格个数count,记录count的最大值
9.对于给定的n,从集合{1}开始,将其添加到ps中,i=2,将ps1设置为空,对于ps的每一个元素s(含1i-1个元素),在其0i-1的位置上插入2,构成新的集合,放到ps中。用vector表示一个集合元素,用vector
10.将二进制位与幂集对应起来,n的幂集个数为2的n次方
关键代码 1-1
#include
#include
using namespace std;
int solve(int a[],int n)
{
sort(a,a+n);
int min=a[1]-a[0];//将数组中的元素递增排序
for(int i=2;i
int tmp=a[i]-a[i-1];
if(tmp
min=tmp;
}
}
return min;
}
int main()
{
int a[]={2,4,3,6,1,7,12};
int n=sizeof(a)/sizeof(a[0]);
printf(“本数组中最小差值是:%d”,solve(a,n));
return 0;
}
1-2
#include
int solve(int a[],int n)
{
int i,j;
int count=0;//计算逆序数
for(i=0;i
for(j=i+1;j
if(a[i]>a[j])
{
count++;
}
}
}
return count;
}
int main()
{
int a[]={4,1,6,2,8,5};
int n=sizeof(a)/sizeof(a[0]);
printf(“此数组中的逆序数是:%d”,solve(a,n));
}
1-3
#include
int solve(int n)
{
int i,j;
int s=1;
int count=0;
for(i=n;i>=1;i–)
{
s=1;
for(j=i;j>=2;j–)
{
s=js;
}
count+=s;
}
return count;
}
int main()
{
int n;
printf(“请输入正整数n(n>1):”);
scanf("%d",&n);
printf(“结果是:%d”,solve(n));
return 0;
}
1-4.
#include
void solve()
{
int a,b,c,d,e,f;
int y,z;
for(a=1;a<=5;a++)
{
for(b=0;b<=5;b++)
{
for(c=0;c<=5;c++)
{
for(d=1;d<=5;d++)
{
for(e=0;e<=5;e++)
{
for(f=0;f<=5;f++)
{
y=a
z=d100+e*10+f;//兔的脚数
if(y%20&&z%40)
{
if(y/2==z/4)
printf(“鸡有%d只,兔有%d只;鸡的脚有%d只,兔的脚有%d只\n”,y/2,z/4,y,z);
else
{
continue;
}
}
}
}
}
}
}
}
}
int main()
{
printf(“求得鸡和兔的结果是:\n”);
solve();
return 0;
}
1-5
#include
void solve()
{
int a,b,c;
int x;
for(a=1;a<=8;a++)
{
for(b=0;b<=7;b++)
{
for(c=2;c<=9;c++)
{
if(a
{
if(a+b+c!=abc)
{
continue;
}
else
{
x=a100+b10+c;
printf(“此三位数是:%d\n”,x);
}
}
}
}
}
}
int main()
{
solve();
return 0;
}
1-6
#include
void solve()
{
int x,y;//x表示最大人数;y表示船
int z;//z表示空余的座位
for(int y=1;y<=100;y++)//让y从0到100枚举,y可以更大,但结果不变
{
for(z=0;z<=11;z++)
{
if(10y-2==12(y-1)-z)
{
x=10*y-2;
}
}
}
printf(“该年级最多人数是:%d\n”,x);
}
int main()
{
solve();
return 0;
}
1-7.
#include
int Count(int n)//求n的各位数字和
{
int sum=0;
while(n>0)
{
sum+=n%10;
n=n/10;
}
return sum;
}
bool solve(int n)//判断n是不是Smitch数
{
int m=2;
int sum1=Count(n);//计算n的各位数字之和
int sum2=0;
while(n>=m)
{
if(n%m0)//m是n的一个质因数
{
n=n/m;
sum2+=Count(m);//求n的各质因数之和
}
else
m++;//m不是n的质因数,m增加1
}
if(sum1sum2)
return true;
else
return false;
}
int main()
{
int n;
printf(“请输入正整数:”);
while(true)
{
scanf("%d",&n);
n=n+1;
if(n==0) break;
while(!solve(n))//n不是Smitch数时
n++;
printf(“大于您输入的数字的最小Smith数是:%d\n”,n);
}
return 0;
}
1-8
#include
#define MAXN 51
int n;
char board[MAXN][MAXN];
int solve()
{
int count=0;
for(int i=0;i
int countj=1;
for(int j=1;j
if(board[j][i]=board[j-1][i])//判断相邻行的同一列,两个棋格颜色是否相同
countj++;
else
countj=1;
}
if(countj>count)
count=countj;
}
return count;
}
int main()
{
printf(“请输入棋格的行和列数(行数=列数):”);
scanf("%d",&n);
for(int i=0;i
printf("%d\n",solve());
return 0;
}
1-9.
#include
#include
using namespace std;
vector
void Insert(vectors,int i,vector
//在每个集合元素(也是集合)中间插入i得到ps1
{
vector s1;
vector::iterator it;
for(int j=0;j
s1=s;
it=s1.begin()+j;//求出待插入的位置
s1.insert(it,i);//在it位置前插入i
ps1.push_back(s1);//其中一个集合的一个位置已经添加好,添加到ps1中
}
}
void Perm(int n)//求1~n的全排列
{
vector
vector
vector s,s1;//
s.push_back(1);
ps.push_back(s);//添加{1}到ps中
for(int i=2;i<=n;i++)//循环添加1~n
{
ps1.clear();//ps1存放每个小集合中插入i后所有可能的结果
for(it=ps.begin();it!=ps.end();++it)
Insert(*it,i,ps1);//在每个集合元素中间插入i得到ps1
ps=ps1;//i全部插入完成后,将ps1赋值给ps,i+1,得到新的ps1
}
}
void dispps()//反向输出全排列ps
{
vector
vector::iterator sit;//排列集合元素迭代器
for(it=ps.rbegin();it!=ps.rend();++it)
{
for(sit=(*it).begin();sit!=(*it).end();++sit)
printf("%d",*sit);
printf(" “);
}
printf(”\n");
}
int main()
{
int n;
printf(“请输入n:”);
scanf("%d",&n);
printf(“1~%d的全排列结果如下:\n”,n);
Perm(n);
dispps();
return 0;
}
1-10.
#include
using namespace std;
/*
Alogorithm Design
蛮力法
1.直接枚举法求解幂集问题
*/
// 将b表示的二进制加1
// b数组下表从小到大对应从低到高位
int inc(int b[],int n){
for(int i=0;i
else{
b[i] = 1;
break;
}
}
}
void PSet(int a[],int b[],int n){
int pw = (int)pow(2,n);
printf(“1到%d的幂集为:\n”,n);
for(int i=0;i
for(int i=0;i
printf(" %d ",a[i]);
}
cout << “}”;
inc(b,n);
}
cout << endl;
}
int main()
{
int n=3;
int a[10],b[10];
for(int i=0;i
b[i] = 0;
}
PSet(a,b,n);
return 0;
}
测试结果 
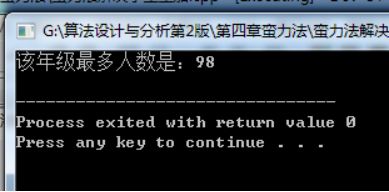

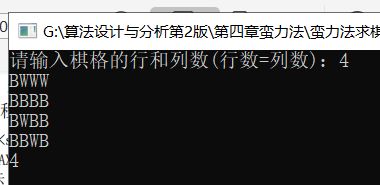

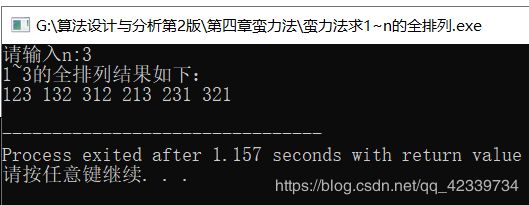
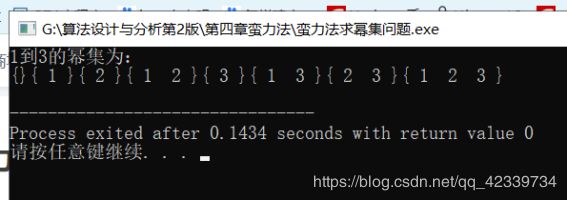
实验心得 通过对蛮力法的练习,理解了蛮力法的工作原理、过程技巧,掌握了常用的暴力法案例(幂级数、全排列等),对蛮力法更深层的问题,掌握的不够熟练,需要反复课下练习。
附录:完整程序代码,依次按照题目序号 1-1 1-2
1-1
#include
#include
using namespace std;
int solve(int a[],int n)
{
sort(a,a+n);
int min=a[1]-a[0];//将数组中的元素递增排序
for(int i=2;i
int tmp=a[i]-a[i-1];
if(tmp
min=tmp;
}
}
return min;
}
int main()
{
int a[]={2,4,3,6,1,7,12};
int n=sizeof(a)/sizeof(a[0]);
printf(“本数组中最小差值是:%d”,solve(a,n));
return 0;
}
1-2
#include
int solve(int a[],int n)
{
int i,j;
int count=0;//计算逆序数
for(i=0;i
for(j=i+1;j
if(a[i]>a[j])
{
count++;
}
}
}
return count;
}
int main()
{
int a[]={3,1,4,5,2};
int n=sizeof(a)/sizeof(a[0]);
printf(“此数组中的逆序数是:%d”,solve(a,n));
}
1-3
#include
int solve(int n)
{
int i,j;
int s=1;
int count=0;
for(i=n;i>=1;i–)
{
s=1;
for(j=i;j>=2;j–)
{
s=js;
}
count+=s;
}
return count;
}
int main()
{
int n;
printf(“请输入正整数n(n>1):”);
scanf("%d",&n);
printf(“结果是:%d”,solve(n));
return 0;
}
1-4
#include
void solve()
{
int a,b,c,d,e,f;
int y,z;
for(a=1;a<=5;a++)
{
for(b=0;b<=5;b++)
{
for(c=0;c<=5;c++)
{
for(d=1;d<=5;d++)
{
for(e=0;e<=5;e++)
{
for(f=0;f<=5;f++)
{
y=a
z=d100+e*10+f;//兔的脚数
if(y%20&&z%40)
{
if(y/2==z/4)
printf(“鸡有%d只,兔有%d只;鸡的脚有%d只,兔的脚有%d只\n”,y/2,z/4,y,z);
else
{
continue;
}
}
}
}
}
}
}
}
}
int main()
{
printf(“求得鸡和兔的结果是:\n”);
solve();
return 0;
}
1-5.
#include
void solve()
{
int a,b,c;
int x;
for(a=1;a<=8;a++)
{
for(b=0;b<=7;b++)
{
for(c=2;c<=9;c++)
{
if(a
{
if(a+b+c!=abc)
{
continue;
}
else
{
x=a100+b10+c;
printf(“此三位数是:%d\n”,x);
}
}
}
}
}
}
int main()
{
solve();
return 0;
}
1-6.
#include
void solve()
{
int x,y;//x表示最大人数;y表示船
int z;//z表示空余的座位
for(int y=1;y<=100;y++)//让y从0到100枚举,y可以更大,但结果不变
{
for(z=0;z<=11;z++)
{
if(10y-2==12(y-1)-z)
{
x=10*y-2;
}
}
}
printf(“该年级最多人数是:%d\n”,x);
}
int main()
{
solve();
return 0;
}
1-7.
#include
int Count(int n)//求n的各位数字和
{
int sum=0;
while(n>0)
{
sum+=n%10;
n=n/10;
}
return sum;
}
bool solve(int n)//判断n是不是Smitch数
{
int m=2;
int sum1=Count(n);//计算n的各位数字之和
int sum2=0;
while(n>=m)
{
if(n%m0)//m是n的一个质因数
{
n=n/m;
sum2+=Count(m);//求n的各质因数之和
}
else
m++;//m不是n的质因数,m增加1
}
if(sum1sum2)
return true;
else
return false;
}
int main()
{
int n;
printf(“请输入正整数:”);
while(true)
{
scanf("%d",&n);
n=n+1;
if(n==0) break;
while(!solve(n))//n不是Smitch数时
n++;
printf(“大于您输入的数字的最小Smith数是:%d\n”,n);
}
return 0;
}
1-8.
#include
#define MAXN 51
int n;
char board[MAXN][MAXN];
int solve()
{
int count=0;
for(int i=0;i
int countj=1;
for(int j=1;j
if(board[j][i]=board[j-1][i])//判断相邻行的同一列,两个棋格颜色是否相同
countj++;
else
countj=1;
}
if(countj>count)
count=countj;
}
return count;
}
int main()
{
printf(“请输入棋格的行和列数(行数=列数):”);
scanf("%d",&n);
for(int i=0;i
printf("%d\n",solve());
return 0;
}
1-9.
#include
#include
using namespace std;
vector
void Insert(vectors,int i,vector
//在每个集合元素(也是集合)中间插入i得到ps1
{
vector s1;
vector::iterator it;
for(int j=0;j
s1=s;
it=s1.begin()+j;//求出待插入的位置
s1.insert(it,i);//在it位置前插入i
ps1.push_back(s1);//其中一个集合的一个位置已经添加好,添加到ps1中
}
}
void Perm(int n)//求1~n的全排列
{
vector
vector
vector s,s1;//
s.push_back(1);
ps.push_back(s);//添加{1}到ps中
for(int i=2;i<=n;i++)//循环添加1~n
{
ps1.clear();//ps1存放每个小集合中插入i后所有可能的结果
for(it=ps.begin();it!=ps.end();++it)
Insert(*it,i,ps1);//在每个集合元素中间插入i得到ps1
ps=ps1;//i全部插入完成后,将ps1赋值给ps,i+1,得到新的ps1
}
}
void dispps()//反向输出全排列ps
{
vector
vector::iterator sit;//排列集合元素迭代器
for(it=ps.rbegin();it!=ps.rend();++it)
{
for(sit=(*it).begin();sit!=(*it).end();++sit)
printf("%d",*sit);
printf(" “);
}
printf(”\n");
}
int main()
{
int n;
printf(“请输入n:”);
scanf("%d",&n);
printf(“1~%d的全排列结果如下:\n”,n);
Perm(n);
dispps();
return 0;
}
1-10.
#include
using namespace std;
/*
Alogorithm Design
蛮力法
1.直接枚举法求解幂集问题
*/
// 将b表示的二进制加1
// b数组下表从小到大对应从低到高位
int inc(int b[],int n){
for(int i=0;i
else{
b[i] = 1;
break;
}
}
}
void PSet(int a[],int b[],int n){
int pw = (int)pow(2,n);
printf(“1到%d的幂集为:\n”,n);
for(int i=0;i
for(int i=0;i
printf(" %d ",a[i]);
}
cout << “}”;
inc(b,n);
}
cout << endl;
}
int main()
{
int n=3;
int a[10],b[10];
for(int i=0;i
b[i] = 0;
}
PSet(a,b,n);
return 0;
}
项目 比例 成绩
学习态度 10% 积极 一般 较差
算法设计及结果 50% 功能正确 功能基本正确 错误
内容完整性 20% 完整 基本完整 不完整
报告规范性 20% 规范 基本规范 不符合要求
成绩