自定义代码实现UserCF——基于用户的协同过滤算法

一、什么是基于用户协同过滤算法

• 我觉得概念讲高大上了，并没有什么用，反而还难以理解。我就用通俗的语言来描述一下这个算法的逻辑吧。这个算法的核心就是这样的：当前如果有一个用户 A 他正在等待被推荐，这时我们就会找出平时的行为和 A 相似的用户 B ,然后我们再讲用户 B 在意或者感兴趣的且 A 还没浏览过的商品推荐给 A ;这就是基于用户的协同过滤算法。

二、如何计算相似度

• 在前面我们了解到了UserCF的算法逻辑了之后，可能你会发现概念中有一个很重要的点就是，计算与A相似的用户，我们用什么一个标准来衡量两个用户的相似程度了；其实已经引出概念了，我们就是需要用相似度来表示两个用户之间的相似程度，但是相似度该如何计算呢？
• 先别急，我们先来想想如果要描述一个人该怎么描述，当然是用一些这个人的特征来描述，对吧。我们先来看个用户的特征表

用户	游戏	学习
A	7	7
B	6	8
C	1	10
D	9	1

• 上面这个中的数字代表各个用户对学习和游戏的看法（也可以看做是评分）满分是10分，我们可以很容易的就把上面的数据加载到图中来：
  
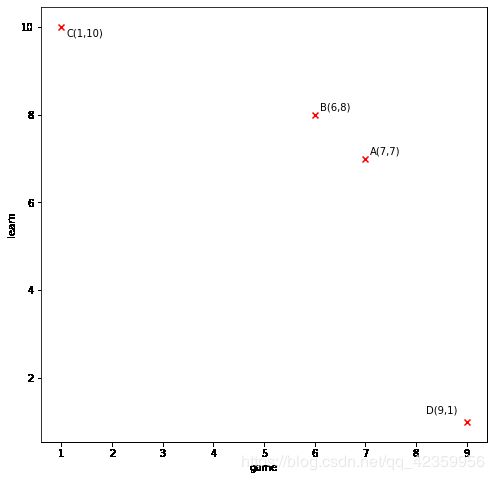
  把图画出来了和你可以很容易的看出 AB 两点挨得最近，也就是 B 与 A 相较于其他的点与 A 的相似度最高，那么如何计算相似度呢？上面都已经说了是挨得比较近，挨得比较近指得是是很么，肯定就是距离了呗，那距离公式就多了，我们平时最常用的就是欧式距离$\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$，这里我们评判用户的特征就只用两个方面，所以就是一个二维，但在实际场景当中，往往用于衡量一个用户有很多的特征俩描述，这时我们如果还想使用欧氏距离，就要把它推导至N维，也就是这样：
  $$Distance(X,Y)=\sqrt{\sum _{i=0}^n{(x_1-y2)}^2}$$
  至于如何公式的推导，想进一步了解的小伙伴可以看博主往期专门讲距离公式的博文，上面有具体的推导过程， 以及其他的一些常用的距离公式算法推导，跳转地址
• 有了上面的概念，我们就知道，我们可以使用两个用户之间的 ‘特征距离‘ 来衡量用户的的相似度了，不过你先要明确一个概念就是，用户的特征距离值越大（也可以说两个用户离得越远）那么两个用户的相似度也就越小，意思就是距离是和相似度呈反比的。

三、算法思路

• 1、首先我们就需要将用户的一些特征数据转换成数值来衡量，因为毕竟计算机还是比较擅长于数值的处理。
  例如现在有一份观影数据表，表的含义就是各个用户的观影情况，以及对此电影的打分。

  用户名	观影名称	评分
  A	老炮儿	3.5
  A	唐人街探案	1.0
  B	老炮儿	2.5
  B	唐人街探案	3.5
  B	星球大战	3.0
  B	寻龙诀	3.5
  B	神探夏洛克	2.5
  B	小门神	3.0
  C	老炮儿	3.0
  C	唐人街探案	3.5
  C	星球大战	1.5
  C	寻龙诀	5.0
  C	神探夏洛克	3.0
  C	小门神	3.5
  D	老炮儿	2.5
  D	唐人街探案	3.5
  D	寻龙诀	3.5
  D	神探夏洛克	4.0
  E	老炮儿	3.5
  E	唐人街探案	2.0
  E	星球大战	4.5
  E	神探夏洛克	3.5
  E	小门神	2.0
  F	老炮儿	3.0
  F	唐人街探案	4.0
  F	星球大战	2.0
  F	寻龙诀	3.0
  F	神探夏洛克	3.0
  F	小门神	2.0
  G	老炮儿	4.5
  G	唐人街探案	1.5
  G	星球大战	3.0
  G	寻龙诀	5.0
  G	神探夏洛克	3.5

  上面的表有一个很关键的指标就是评分，可以通过这个值的大小来看出用户对该电影的喜爱度（也可以说是感兴趣程度），我们都知道描述一个用户的特征是多维度的，而且作为分析需要，我们描述各个用户都应该从相同的维度来描述。根据上面的思路，再根据表的结构，我们可以将上面的表转换成下面的格式:

  *	神探夏洛克	小门神	唐人街探案	寻龙诀	老炮儿	星球大战
  A	0	0	1.0	0	3.5	0
  B	2.5	3.0	3.5	3.5	2.5	3.0
  C	3.0	3.5	3.5	5.0	3.0	1.5
  D	4.0	0	3.5	3.5	2.5	0
  E	3.5	2.0	2.0	0	3.5	4.5
  F	3.0	2.0	4.0	3.0	3.0	2.0
  G	3.5	0	1.5	5.0	4.5	3.0

  转换成上面这个表的思路其实就是现将所有（不重复的电影名列出来）然后如果该用户没看过该电影，我们就将该用户对该电影的评分置为 0，通过这样的转换我们就将用户的特征由不规则的文本类型，转换成了标准的数值特征，例如：用户 A 的特征向量就为$V_A=<0,0,1.0,0,3.5,0>$

• 2、现在有了特征矩阵，我们就可以来计算用户之间的距离了，为了后续计算的方便，我们不妨将所有用户之间的距离都计算一遍，也就是计算一个距离矩阵：

  *	A	B	C	D	E	F	G
  A	$\infty$	6.61	7.42	5.96	6.12	5.94	6.89
  B	6.61	$\infty$	2.29	4.5	4.44	1.73	4.5
  C	7.42	2.29	$\infty$	4.24	6.24	2.6	4.58
  D	5.96	4.5	4.24	$\infty$	6.32	3.12	4.42
  E	6.12	4.44	6.24	6.32	$\infty$	4.44	5.7
  F	5.94	1.73	2.6	3.12	4.44	$\infty$	4.21
  G	6.89	4.5	4.58	4.42	5.7	4.21	$\infty$

  我们随便找两个用户来作为示例，例如要计算AB两个用户之间的距离，那么我们读前一个表可以知道$V_A=<0,0,1.0,0,3.5,0>,V_B=<2.5,3.0,3.5,3.5,2.5,3.0>$,那么AB之间的距离可以表示为
  $$D_{AB}=\sqrt{(0-2.5{)}^2+(0-3.0{)}^2+(1-3.5{)}^2+(0-3.5{)}^2+(3.5-2.5{)}^2+(0-3.0{)}^2}=6.61$$
  因为用户和自己求距离必然会是0，但是为了后面我们要选取相似的用户时不选到自己，那么我们把用户和自己求距离这里置为无限大即可。

• 下只能在我们引入UserCF算法公式：
  $$p(u,i)=\sum _{v\in S(u,k)\cap N(i)}{w}_{uv}{r}_{vi}$$
  先来解释一下公式中的参数含义：
  (1) $S(u,k)$ 就是计算和用户 u 最相似的 k 个用户
  (2) $N(i)$表示对电影 i 有过评分记录的用户集合
  (3) $w_{uv}表示用户u和用户v之间的相似度$
  (4) $r_{vi}$表示用户 v 对电影 i 喜好度，也就是用户 v 对 电影i的评分
  然后通过这个公式计算出来值就是推荐指数（为了方便，我们这里就用距离代表用户之间的相似度，所以最后求出来的推荐度应该是越小，该物品就越值得推荐）

四、代码实现

1、准备数据

import numpy as np

movies_data_dict = {
    'A': {'老炮儿':3.5,'唐人街探案': 1.0},
    'B': {'老炮儿':2.5,'唐人街探案': 3.5,'星球大战': 3.0, '寻龙诀': 3.5, '神探夏洛克': 2.5, '小门神': 3.0},
    'C': {'老炮儿':3.0,'唐人街探案': 3.5,'星球大战': 1.5, '寻龙诀': 5.0, '神探夏洛克': 3.0, '小门神': 3.5},
    'D': {'老炮儿':2.5,'唐人街探案': 3.5,'寻龙诀': 3.5, '神探夏洛克': 4.0},
    'E': {'老炮儿':3.5,'唐人街探案': 2.0,'星球大战': 4.5, '神探夏洛克': 3.5,'小门神': 2.0},
    'F': {'老炮儿':3.0,'唐人街探案': 4.0,'星球大战': 2.0, '寻龙诀': 3.0,'神探夏洛克': 3.0, '小门神': 2.0},
    'G': {'老炮儿':4.5,'唐人街探案': 1.5,'星球大战': 3.0, '寻龙诀': 5.0,'神探夏洛克': 3.5}
    }

2、编写将数据标准化的函数

# 将整个数据集转换成矩阵形式，如果用户没有对该电影进行评分则该位置置为 0
def MoveiesScaler(data):
    movie_index = {}
    i = 0
    for _,ratings in data.items():
        for movie,score in ratings.items():
            if movie_index.get(movie) is None:
                movie_index[movie] = i
                i += 1
    result_data = {}
    for user,ratings in data.items():
        user_ratings = np.zeros(len(movie_index))
        for movie,score in ratings.items():
            user_ratings[movie_index[movie]] = score
        result_data[user] = user_ratings
    return movie_index,result_data

3、编写特征距离计算函数

# 计算两个用户的欧式距离
def EuclideanDistance(feature1,feature2):
    return np.sqrt(np.sum(np.power(feature1-feature2,2)))

# 计算所有用户俩俩之间的距离，也就是距离矩阵，用户对自己求距离时将距离置为无穷大方便后续处理
def DistanceMatrix(user_dict):
    result_matrix = np.zeros((len(user_dict),len(user_dict)))
    user_index = dict(zip(user_dict.keys(),range(len(user_dict))))
    features = list(user_dict.values())
    for r in range(len(features)):
        for c in range(r,len(features)):
            if c == r:
                result_matrix[r][c] = np.Inf
            else:
                ed = EuclideanDistance(features[r],features[c])
                result_matrix[r][c] = ed
                result_matrix[c][r] = ed
    return user_index,result_matrix

4、$S(u,k)$ 和用户u最相似的k个用户

def similarity_max_k(similarity_matrix,user_index,u,k):
    similarity_list = similarity_matrix[user_index[u]]
    user_sim_map = dict(zip(similarity_list.tolist(),user_index.keys()))
    least_k_keys = sorted(user_sim_map)[:k]
    least_k = set({user_sim_map[k] for k in least_k_keys})
    return least_k

5、$N(i)$对电影 i 有过评分的用户

def user_with_item(data_sets,i):
    user_set = set()
    for user,ratings in data_sets.items():
        if(ratings[i] != 0):
            user_set.add(user)
    return user_set

6、$r_{vi}$ 用户 v 对 电影i的评分

def interest_degree(data_sets,v,i):
    return data_sets[v][i]

7、将前面的函数组装起来就是UserCF的公式实现

def recommended_score(datasets,u,k,i):
    user_index,similarity_matrix = DistanceMatrix(data_sets)
    similarity_k_set = similarity_max_k(similarity_matrix,user_index,u,k)
    user_item_set = user_with_item(data_sets,i)
    iter_set = similarity_k_set & user_item_set
    
    result = 0
    
    for v in iter_set:
        v_i = user_index[v]
        u_i = user_index[u]
        w = similarity_matrix[v_i][u_i]
        result += (w*interest_degree(data_sets,v,i))
    return result

8、查看各个商品对用户的推荐度

for i in range(6):
    print(recommended_score(movies_data_dict,"A",2,i))

out:

32.70698224032311
44.60234092774856
11.874342087037917
38.6651698842296
41.64426370618284
11.874342087037917

我们可以寻找出推荐度最小的（因为推荐度公式那儿我们已经换成了距离来计算，所以要越小越好）那几个商品，且用户A还没有看过的，那么我们就可以把这些商品推荐给他。
补充：我们可以使用不同的距离公式来计算两个用户之间的特征距离，比较好的就是 Jaccard（杰卡德距离），余弦距离您可以尝试使用不同的距离计算公式来尝试，然后调整您推荐算法的准确率。