蓝桥杯-带分数（C语言）

9. 标题：带分数
可以表示为带分数的形式：100 = 3 + 69258 / 714

还可以表示为：100 = 82 + 3546 / 197

注意特征：带分数中，数字1~9分别出现且只出现一次（不包含0）。

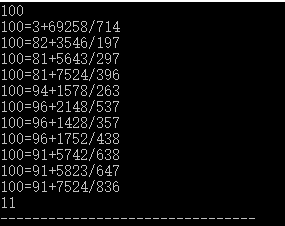
类似这样的带分数，100 有 11 种表示法。

题目要求：
从标准输入读入一个正整数N (N<1000*1000)
程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
注意：不要求输出每个表示，只统计有多少表示法！

例如：
用户输入：
程序输出：

再例如：
用户输入：
程序输出：

解题思路（全排列）

如果对全排列算法不同可以看看本人的另两篇博客。

[非递归全排列]https://blog.csdn.net/qq_42552533/article/details/88609886
[递归全排列]https://blog.csdn.net/qq_42552533/article/details/88606550

将“123456789”全排列，然后用a,b,c划分，我们这里主要讲要怎么划分：

我们规定a在最前面，b在中间，c在尾部

这样我们可以知道a的头部就是list的第一位list[0]，a的尾部就是b的头部（不能确定）

b的尾部则是c的头部（也不能确定），但是我们知道c的尾部一定是list[8]。

然后又有number = a + b / c 等式成立。变形一下：b = (number - a) * c。

好了，注意，根据乘法原理我们可以推出b的尾部数字（设为BLast）。

BLast=((number-a)*list[8])%10; //确定b最后一个数字。

最后为了程序优化，我们剪掉一些不可能的情况。

下面我们对a,b,c的区间进行分析：
number = a + b / c
a为带分数的左边，（1<= a <= 1000,000）这个范围没错吧？1000,000为题目规定范围。我们用for循环人为设定a区间的尾部。

b为带分数的上部，这里隐含条件（b % c == 0）必须为整数。所以b>=c这点是必须的，由于我们划分的是区间，

所以区间长度就能近似的表示数值的大小了，区间越长，说明数值位数越多，肯定值越大，所以b的区间长度就必须不小于c的区间长度。

也就是说a后面剩下的list长度b要占一半以上。因为b的最后一位我们已经算出来了，所以我们需要匹配最后一位的位置，就能划分出a,b,c区间。

说了这么一大堆，我自己都搞晕了。放个例子出来溜溜，还是以上面那个排列来说明。

示例：3+69258 / 714 （number = 100）

abc = 369258714

我们是这么来划分的：
第一步：人为划分a（如：（0,1）），即a = 3

第二步：计算出bLast=((number-a)*list[8])%10 = ((100 - 3) * 4)%10 = 8

第三步：a = （0,1）那么bc则是（2,8），那么b的最后一位我们从(8-2)/2 = 3，也就是从list[3] = 2开始找起（直接跳过前面不可能情况） 369-258714

第四步：判断BLast == list[i]，当找到了b的尾部的时候，我们就开始检查组合的合理性：它将满足条件number == a+b/c且b%c==0（如果合理）

第五步：如果合理则将情况种数+1同时跳出for循环，进入递归找下一组排列。

如果不合理，则将a划分区间长度+1，a = （0,2），即a = 36，然后再确定b的尾部BLast…

下面是一个简单的图分析：

程序代码如下：

#include
#include

int count = 0 , number = 0 , x = 0;

/*交换*/
void swap(int *a,int *b )
{
	int temp = *a;
	*a = *b;
	*b = temp;
}

/*将数字区间转换成数字*/
int GetNum(int arry[],int f,int r)
{
	int num=0;
	for(int i=f;i<=r;i++)
	{
		num = arry[i] + num * 10;
	}
	return num;
}

//进行全排列并对每种排列结果进行处理 
void Allarrange(int arry[],int s,int length)
{
	if( s == length )
	{
		int a,b,c,BLast;
		for(int i = 0 ; i < x ; i++ )
		{
			a = GetNum(arry,0,i);
			BLast = ((number-a)*arry[8])%10; //找到b尾部的值 
			
			for(int j=i+(8-i)/2 ; j < 8 ; j++)
			{
				if(BLast == arry[j])         //找到b尾部
				{
					b = GetNum(arry,i+1,j);  //将arry数组中的[i+1-j]转化为数字，赋值给b
					c = GetNum(arry,j+1,8);  //将arry数组中的[j+1-8]转化为数字，赋值给c
				
					if( b % c == 0 && a + b / c == number )//判断合理性 
					{
						printf("%d=%d+%d/%d\n",number,a,b,c);
						++count;
					}
					break;
				}
			}
		}
	}
	else
	{
		for(int i=s;i<=length;i++)
		{
			swap(&arry[s],&arry[i]);
			Allarrange(arry,s+1,length);
			swap(&arry[s],&arry[i]);
		}
	}
}

int main()
{
	int arry[]={1,2,3,4,5,6,7,8,9};
	int len=sizeof(arry)/sizeof(arry[0]);
	scanf("%d",&number);
	int temp =number;
	while(temp!=0)
	{
		x++;             //统计输入number的位数 
		temp /= 10; 
	}
	Allarrange(arry,0,len-1);
	printf("%d",count);
	return 0;
}

运行截图：