numpy中dot()、matmul()以及multiply()的区别

前文

简单的说，这三个方法各有各的特点，他们主要是进行Numpy的矩阵乘法的，但是，要知道，矩阵乘法里面也是有区分的，主要分为元素及乘法和矩阵乘积

那现在我们首先来写一下区分

np.dot

函数	语法	作用	备注
dot	dot(t1，t2)	若t1、t2均为一维数组，则是普通的内积	结果为一个数
dot	dot(t1,t2)	若t1、t2为矩阵，则是矩阵乘法	前一个矩阵的列数要与后一个矩阵的行数相等
dot	dot(t1,scalar)	元素级乘法	遵循广播原则，scalar作用于所有的元素上

np.matmul

函数	语法	作用	备注
matmul	matmul(t1,t2)	t1、t2均为矩阵或数组	此方法只能进行矩阵或数组乘法，不能进行元素级乘法

np.multiply

函数	语法	作用	备注
multiply	multiply(t1,scalar)	元素级乘法	同样遵循广播原则，scalar作用于所有的元素上
multiply	multiply(t1,t2)	对应元素相乘	详情请点击此处(参考广播原则成立的三种方法)

分析

np.dot

dot()是比较复杂的一个，因为参数的不同可以实现等同于np.matmul() 或者 np.multiply()的作用

• 当 t1 和 t2 都是一维数组的时候，结果就是普通的內积，可以使用np.matmul 或者 a @ b 得到相同的结果
  $$a\ast b=\sum _{i=1}^n{a}_i{b}_i=a_1{b}_1+a_2{b}_2+a_3{b}_3+......a_n{b}_n$$
• 当 t1 和 t2 都是二维的时候，运算等同于矩阵乘法，同样可以使用np.matmul 或者 a @ b 得到相同的答案

代码演示

准备数据

#一维 1行6列的数组
In [13]: t1
Out[13]: array([1, 2, 3, 4, 5, 6])

#二维 6行6列的数组
In [14]: t2
Out[14]:
array([[ 1,  2,  3,  4,  5,  6],
       [ 7,  8,  9, 10, 11, 12],
       [13, 14, 15, 16, 17, 18],
       [19, 20, 21, 22, 23, 24],
       [25, 26, 27, 28, 29, 30],
       [31, 32, 33, 34, 35, 36]])

实际操作

#矩阵乘法
In [15]: np.dot(t1,t2)
Out[15]: array([441, 462, 483, 504, 525, 546])

#元素级乘法
In [16]: np.dot(t1,2)
Out[16]: array([ 2,  4,  6,  8, 10, 12])

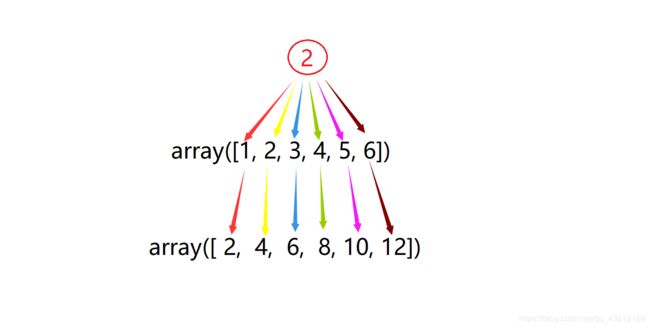
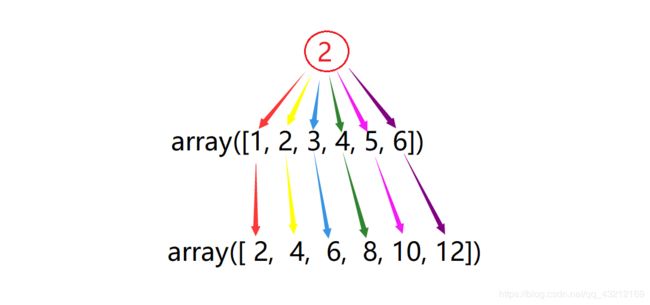
画图解释

数组与数组之间的乘积

数组与标量的元素级乘法

np.matmul

主要实现数组与数组之间的乘积或矩阵乘法，当计算数组或矩阵与标量的乘积时会报错

代码演示

准备数据

#一维 1行6列的数组
In [13]: t1
Out[13]: array([1, 2, 3, 4, 5, 6])

#二维 6行6列的数组
In [14]: t2
Out[14]:
array([[ 1,  2,  3,  4,  5,  6],
       [ 7,  8,  9, 10, 11, 12],
       [13, 14, 15, 16, 17, 18],
       [19, 20, 21, 22, 23, 24],
       [25, 26, 27, 28, 29, 30],
       [31, 32, 33, 34, 35, 36]])

实际操作

#数组 t1 与 t2 的乘积
In [19]: np.matmul(t1,t2)
Out[19]: array([441, 462, 483, 504, 525, 546])

#计算 数组 与 元素 之间的乘法，会报错
In [20]: np.matmul(t1,2)
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-20-8a0e145277d0> in <module>()
----> 1 np.matmul(t1,2)

ValueError: matmul: Input operand 1 does not have enough dimensions (has 0, gufunc core with signature (n?,k),(k,m?)->(n?,m?) requires 1)

np.multiply

主要实现数组与元素之间的乘积或数组与数组之间对应元素相乘

代码演示

准备数据

#一维 1行6列的数组
In [13]: t1
Out[13]: array([1, 2, 3, 4, 5, 6])

#二维 6行6列的数组
In [14]: t2
Out[14]:
array([[ 1,  2,  3,  4,  5,  6],
       [ 7,  8,  9, 10, 11, 12],
       [13, 14, 15, 16, 17, 18],
       [19, 20, 21, 22, 23, 24],
       [25, 26, 27, 28, 29, 30],
       [31, 32, 33, 34, 35, 36]])

实际操作

#使用 multiply 方法计算数组与数组之间对应元素相乘结果
In [23]: np.multiply(t1,t2)
Out[23]:
array([[  1,   4,   9,  16,  25,  36],
       [  7,  16,  27,  40,  55,  72],
       [ 13,  28,  45,  64,  85, 108],
       [ 19,  40,  63,  88, 115, 144],
       [ 25,  52,  81, 112, 145, 180],
       [ 31,  64,  99, 136, 175, 216]])

#使用 multiply 方法计算数组与标量的相乘结果
In [24]: np.multiply(t1,2)
Out[24]: array([ 2,  4,  6,  8, 10, 12])

画图解释

数组与数组之间对应元素相乘

数组与标量的相乘

总结

• np.dot()方法既能做数组与数组之间乘积运算，也可以做数组与标量之间的乘积运算，但是，要记住，np.dot()的数组和数组的乘法，是交叉乘法

• np.matmul 只能做数组与数组之间的交叉乘法，当使用此方法做数组与标量的乘法时，会报错

• np.multiply 能做数组与数组的乘法，但是这个乘法是数组 t1 与 数组 t2 对应元素相乘 ,除此之外，此方法还可以做数组与标量之间的乘法，标量(scalar)作用于数组所有的元素上(广播机制原则)