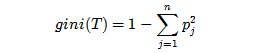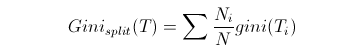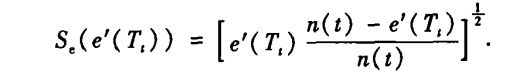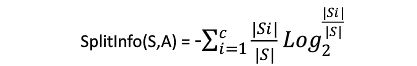C4.5决策树算法介绍
http://blog.sina.com.cn/s/blog_68ffc7a40100urn3.html
1. 算法背景介绍
分类树（决策树）是一种十分常用的分类方法。他是一种监管学习，所谓监管学习说白了很简单，就是给定一堆样本，每个样本都有一组属性和一个类别，这些类别是事先确定的，那么通过学习得到一个分类器，这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。分类本质上就是一个map的过程。C4.5分类树就是决策树算法中最流行的一种。下面给出一个数据集作为算法例子的基础，比如有这么一个数据集，如下：
这个Golf数据集就是我们这篇博客讨论的基础。我们分类的目的就是根据某一天的天气状态，如天气，温度，湿度，是否刮风，来判断这一天是否适合打高尔夫球。
2. 算法描述
确切的说，C4.5不是单个的算法，而是一套算法，C4.5有许多的功能，每个功能都对应着一个算法，这些功能组合起来就形成了一套算法就是C4.5。C4.5分类树构造算法框架如下图：
Figure 1
该算法的框架表述还是比较清晰的，从根节点开始不断得分治，递归，生长，直至得到最后的结果。根节点代表整个训练样本集,通过在每个节点对某个属性的测试验证,算法递归得将数据集分成更小的数据集.某一节点对应的子树对应着原数据集中满足某一属性测试的部分数据集.这个递归过程一直进行下去,直到某一节点对应的子树对应的数据集都属于同一个类为止.Golf数据集对应得到的决策树如下:
Figure 1给出了C4.5分类树构造算法的框架，一些细节并没有阐述。下面就来具体分析一下里面可能面对的问题：
分类树中的测试是怎样的？
分类树中的测试是针对某一个样本属性进行的测试。我们知道，样本的属性有两种，一种是离散变量，一种是连续变量。对于离散变量，这很简单，离散变量对应着多个值，每个值就对应着测试的一个分支，测试就是验证样本对应的属性值对应哪个分支。这样数据集就会被分成几个小组。对于连续变量，所有连续变量的测试分支都是2条，其测试分支分别对应着
，
对应着分支阈值，后面我们来讨论这个分支阈值如何选择。
如何选择测试？
分类树中每个节点对应着测试，但是这些测试是如何来选择呢？C4.5根据信息论标准来选择测试，比如增益（在信息论中，熵对应着某一分布的信息量，其值同时也对应着要完全无损表示该分布所需要的最小的比特数，本质上熵对应着不确定性，可能的变化的丰富程度。所谓增益，就是指在应用了某一测试之后，其对应的可能性丰富程度下降，不确定性减小，这个减小的幅度就是增益，其实质上对应着分类带来的好处）或者增益比（这个指标实际上就等于增益/熵，之所以采用这个指标是为了克服采用增益作为衡量标准的缺点，采用增益作为衡量标准会导致分类树倾向于优先选择那些具有比较多的分支的测试，这种倾向需要被抑制）。算法在进行Tree-Growth时，总是“贪婪得”选择那些信息论标准最高的那些测试。
如何选择连续变量的阈值？
在《分类树中的测试是怎样的？》中提到连续变量的分支的阈值点为
，这阈值如何确定呢？很简单，把需要处理的样本（对应根节点）或样本子集（对应子树）按照连续变量的大小从小到大进行排序，假设该属性对应的不同的属性值一共有N个，那么总共有N-1个可能的候选分割阈值点，每个候选的分割阈值点的值为上述排序后的属性值链表中两两前后连续元素的中点，那么我们的任务就是从这个N-1个候选分割阈值点中选出一个，使得前面提到的信息论标准最大。举个例子，对于Golf数据集，我们来处理温度属性，来选择合适的阈值。首先按照温度大小对对应样本进行排序如下
那么可以看到有13个可能的候选阈值点，比如middle[64,65], middle[65,68]….,middle[83,85]。那么最优的阈值该选多少呢？应该是middle[71,72]，如上图中红线所示。为什么呢？如下计算：
通过上述计算方式，0.939是最大的，因此测试的增益是最小的。（测试的增益和测试后的熵是成反比的，这个从后面的公式可以很清楚的看到）。根据上面的描述，我们需要对每个候选分割阈值进行增益或熵的计算才能得到最优的阈值，我们需要算N-1次增益或熵（对应温度这个变量而言就是13次计算）。能否有所改进呢？少算几次，加快速度。答案是可以该进，如下图
该图中的绿线代表可能的最优分割阈值点，根据信息论知识，像middle[72,75]（红线所示）这个分割点，72,75属于同一个类，这样的分割点是不可能有信息增益的。（把同一个类分成了不同的类，这样的阈值点显然不会有信息增益，因为这样的分类没能帮上忙，减少可能性）
Tree-Growth如何终止?
前面提到Tree-Growth实际上是一个递归过程,那么这个递归什么时候到达终止条件退出递归呢?有两种方式,第一种方式是如果某一节点的分支所覆盖的样本都属于同一类的时候,那么递归就可以终止,该分支就会产生一个叶子节点.还有一种方式就是，如果某一分支覆盖的样本的个数如果小于一个阈值，那么也可产生叶子节点，从而终止Tree-Growth。
如何确定叶子节点的类？
前面提到Tree-Growth终止的方式有2种，对于第一种方式，叶子节点覆盖的样本都属于同一类，那么这种情况下叶子节点的类自然不必多言。对于第二种方式，叶子节点覆盖的样本未必属于同一类，直接一点的方法就是，该叶子节点所覆盖的样本哪个类占大多数，那么该叶子节点的类别就是那个占大多数的类。
前面《如何选择测试？》提到测试的选择是依据信息论标准，信息论标准有两种，一种是增益，一种是增益比。首先来看看增益Gain的计算。假设随机变量x，它可能属于c个类中的任何一个，通过样本的统计，它分别属于各个类的概率分别为
，那么要想把某一样本进行归类所需要的熵就为
公式1
对于Golf数据集，{PlayGolf？}的熵根据上述公式，就是
上述公式的值为0.940。它的信息论含义就是我要想把PlayGolf？这个信息传递给别人话，平均来讲我至少需要0.940个bit来传递这个信息。C4.5的目标就是经过分类来减小这个熵。那么我们来依次考虑各个属性测试，通过某一属性测试我们将样本分成了几个子集，这使得样本逐渐变得有序，那么熵肯定变小了。这个熵的减小量就是我们选择属性测试的依据。还是以Golf数据集为例，Outlook的增益Gain(Outlook),其公式如下：
它的实质是把数据集D根据某一属性测试分成v个子集，这使得数据集D变得有序，使得数据集D的熵变小了。分组后的熵其实就是各个子集的熵的权重和。通过计算我们得到Gain(Outlook)=0.940-0.694=0.246，Gain(Windy)=0.940-0.892=0.048….
可以得到第一个测试属性是Outlook。需要注意的是，属性测试是从数据集中包含的所有属性组成的候选属性中选择出来的。对于所在节点到根节点的路径上所包含的属性（我们称之为继承属性），其实根据公式很容易得到他们的熵增益是0，因此这些继承属性完全不必考虑，可以从候选属性中剔除这些属性。
到这里似乎一切都很完美，增益这个指标非常得make sense，但是其实增益这个指标有一个缺点。我们来考虑Golf数据集中的Day这个属性（我们假设它是一个真属性，实际上很可能大家不会把他当做属性），Day有14个不同的值，那么Day的属性测试节点就会有14个分支，很显然每个分支其实都覆盖了一个“纯”数据集（所谓“纯”，指的就是所覆盖的数据集都属于同一个类），那么其熵增益显然就是最大的，那么Day就默认得作为第一个属性。之所以出现这样的情况，是因为增益这个指标天然得偏向于选择那些分支比较多的属性，也就是那些具有的值比较多的那些属性。这种偏向性使我们希望克服的，我们希望公正地评价所有的属性。因此又一个指标被提出来了Gain Ratio-增益比。某一属性A的增益比计算公式如下：
Gain(A)就是前面计算的增益，而SplitInfo(A)计算如下：
公式2
与公式1进行比较，你会发现，SplitInfo(A)实际上就是属性A的熵，只不过这个熵有所不同，他不是样本最终分类{PlayGolf？}的熵，而是对应属性分组{A?}的熵，它反映的是属性A本身的信息量。通过计算我们很容易得到GainRatio(Outlook)=0.246/1.577=0.156。增益比实际上就是对增益进行了归一化，这样就避免了指标偏向分支多的属性的倾向。
通过上述方法得到了决策树，这一切看起来都很完美，但是这还不够。决策树能够帮助我们对新出现的样本进行分类，但还有一些问题它不能很好得解决。比如我们想知道对于最终的分类，哪个属性的贡献更大？能否用一种比较简洁的规则来区分样本属于哪个类？等等。为了解决这些问题，基于产生的决策树，各位大牛们又提出了一些新的方法。
3. C4.5的功能
3.1 决策树的剪枝
决策树为什么要剪枝？原因就是避免决策树“过拟合”样本。前面的算法生成的决策树非常的详细而庞大，每个属性都被详细地加以考虑，决策树的树叶节点所覆盖的训练样本都是“纯”的。因此用这个决策树来对训练样本进行分类的话，你会发现对于训练样本而言，这个树表现堪称完美，它可以100%完美正确得对训练样本集中的样本进行分类（因为决策树本身就是100%完美拟合训练样本的产物）。但是，这会带来一个问题，如果训练样本中包含了一些错误，按照前面的算法，这些错误也会100%一点不留得被决策树学习了，这就是“过拟合”。C4.5的缔造者昆兰教授很早就发现了这个问题，他作过一个试验，在某一个数据集中，过拟合的决策树的错误率比一个经过简化了的决策树的错误率要高。那么现在的问题就来了，如何在原生的过拟合决策树的基础上，通过剪枝生成一个简化了的决策树？
第一种方法，也是最简单的方法，称之为基于误判的剪枝。这个思路很直接，完全的决策树不是过度拟合么，我再搞一个测试数据集来纠正它。对于完全决策树中的每一个非叶子节点的子树，我们尝试着把它替换成一个叶子节点，该叶子节点的类别我们用子树所覆盖训练样本中存在最多的那个类来代替，这样就产生了一个简化决策树，然后比较这两个决策树在测试数据集中的表现，如果简化决策树在测试数据集中的错误比较少，并且该子树里面没有包含另外一个具有类似特性的子树（所谓类似的特性，指的就是把子树替换成叶子节点后，其测试数据集误判率降低的特性），那么该子树就可以替换成叶子节点。该算法以bottom-up的方式遍历所有的子树，直至没有任何子树可以替换使得测试数据集的表现得以改进时，算法就可以终止。
第一种方法很直接，但是需要一个额外的测试数据集，能不能不要这个额外的数据集呢？为了解决这个问题，于是就提出了悲观剪枝。该方法剪枝的依据是训练样本集中的样本误判率。我们知道一颗分类树的每个节点都覆盖了一个样本集，根据算法这些被覆盖的样本集往往都有一定的误判率，因为如果节点覆盖的样本集的个数小于一定的阈值，那么这个节点就会变成叶子节点，所以叶子节点会有一定的误判率。而每个节点都会包含至少一个的叶子节点，所以每个节点也都会有一定的误判率。悲观剪枝就是递归得估算每个内部节点所覆盖样本节点的误判率。剪枝后该内部节点会变成一个叶子节点，该叶子节点的类别为原内部节点的最优叶子节点所决定。然后比较剪枝前后该节点的错误率来决定是否进行剪枝。该方法和前面提到的第一种方法思路是一致的，不同之处在于如何估计剪枝前分类树内部节点的错误率。
悲观剪枝的思路非常巧妙。把一颗子树（具有多个叶子节点）的分类用一个叶子节点来替代的话，误判率肯定是上升的（这是很显然的，同样的样本子集，如果用子树分类可以分成多个类，而用单颗叶子节点来分的话只能分成一个类，多个类肯定要准确一些）。于是我们需要把子树的误判计算加上一个经验性的惩罚因子。对于一颗叶子节点，它覆盖了N个样本，其中有E个错误，那么该叶子节点的错误率为（E+0.5）/N。这个0.5就是惩罚因子，那么一颗子树，它有L个叶子节点，那么该子树的误判率估计为
。这样的话，我们可以看到一颗子树虽然具有多个子节点，但由于加上了惩罚因子，所以子树的误判率计算未必占到便宜。剪枝后内部节点变成了叶子节点，其误判个数J也需要加上一个惩罚因子，变成J+0.5。那么子树是否可以被剪枝就取决于剪枝后的错误J+0.5在
的标准误差内。
对于样本的误差率e，我们可以根据经验把它估计成各种各样的分布模型，比如是二项式分布，比如是正态分布。我们以二项式分布为例，啰嗦几句来分析一下。什么是二项分布，在n次独立重复试验中，设事件A发生的次数为X，如果每次试验中中事件A发生的概率是p，那么在n次独立重复试验中，事件A恰好发生k次的概率是
其概率期望值为np，方差为np(1-p)。比如投骰子就是典型的二项分布，投骰子10次，掷得4点的次数就服从n=10，p=1/6的二项分布。
如果二项分布中n=1时，也就是只统计一次，事件A只可能有两种取值1或0，那么事件A的值所代表的分布就是伯努利分布。B(1,p)~f(1;1,p)就是伯努利分布，伯努利分布式是二项分布的一种特殊形式。比如投硬币，正面值为1，负面值为0，那么硬币为正面的概率为p=0.5，该硬币值就服从概率为0.5的伯努利分布。
当n趋于无限大时，二项式分布就正态分布，如下图。
那么一棵树错误分类一个样本值为1，正确分类一个样本值为0，该树错误分类的概率（误判率）为e（e为分布的固有属性,可以通过
统计出来），那么树的误判次数就是伯努利分布，我们可以估计出该树的误判次数均值和方差：
把子树替换成叶子节点后，该叶子的误判次数也是一个伯努利分布，其概率误判率e为(E+0.5)/N，因此叶子节点的误判次数均值为
那么，如果子树可以被叶子节点替代，它必须满足下面的条件：
这个条件就是剪枝的标准。根据置信区间，我们设定一定的显著性因子，我们可以估算出误判次数的上下界。
误判次数也可以被估计成一个正态分布，有兴趣大家可以推导一下。
3.2 连续值属性的改进
相对于那些离散值属性，分类树算法倾向于选择那些连续值属性，因为连续值属性会有更多的分支，熵增益也最大。算法需要克服这种倾向。还记得前面讲得如何克服分类树算法倾向于离散值较多的离散属性么？对了，我们利用增益率来克服这种倾向。增益率也可以用来克服连续值属性倾向。增益率作为选择属性的依据克服连续值属性倾向，这是没有问题的。但是如果利用增益率来选择连续值属性的分界点，会导致一些副作用。分界点将样本分成两个部分，这两个部分的样本个数之比也会影响增益率。根据增益率公式，我们可以发现，当分界点能够把样本分成数量相等的两个子集时（我们称此时的分界点为等分分界点），增益率的抑制会被最大化，因此等分分界点被过分抑制了。子集样本个数能够影响分界点，显然不合理。因此在决定分界点是还是采用增益这个指标，而选择属性的时候才使用增益率这个指标。这个改进能够很好得抑制连续值属性的倾向。当然还有其它方法也可以抑制这种倾向，比如MDL，有兴趣的读者可以自己阅读相关文章。
3.3 处理缺失属性
如果有些训练样本或者待分类样本缺失了一些属性值，那么该如何处理？要解决这个问题，需要考虑3个问题：i)当开始决定选择哪个属性用来进行分支时，如果有些训练样本缺失了某些属性值时该怎么办？ii)一个属性已被选择，那么在决定分支的时候如果有些样本缺失了该属性该如何处理？iii)当决策树已经生成，但待分类的样本缺失了某些属性，这些属性该如何处理？针对这三个问题，昆兰提出了一系列解决的思路和方法。
对于问题i),计算属性a的增益或者增益率时，如果有些样本没有属性a，那么可以有这么几种处理方式：(I)忽略这些缺失属性a的样本。(C)给缺失属性a的样本赋予属性a一个均值或者最常用的的值。(R)计算增益或者增益率时根据缺失属性样本个数所占的比率对增益/增益率进行相应的“打折”。(S)根据其他未知的属性想办法把这些样本缺失的属性补全。
对于问题ii)，当属性a已经被选择，该对样本进行分支的时候，如果有些样本缺失了属性a,那么：(I)忽略这些样本。(C)把这些样本的属性a赋予一个均值或者最常出现的值，然后再对他们进行处理。(R)把这些属性缺失样本，按照具有属性a的样本被划分成的子集样本个数的相对比率，分配到各个子集中去。至于哪些缺失的样本被划分到子集1，哪些被划分到子集2，这个没有一定的准则，可以随机而动。(A)把属性缺失样本分配给所有的子集，也就是说每个子集都有这些属性缺失样本。(U)单独为属性缺失的样本划分一个分支子集。(S)对于缺失属性a的样本，尝试着根据其他属性给他分配一个属性a的值，然后继续处理将其划分到相应的子集。
对于问题iii)，对于一个缺失属性a的待分类样本，有这么几种选择：(U)如果有单独的确实分支，依据此分支。(c)把待分类的样本的属性a值分配一个最常出现的a的属性值，然后进行分支预测。(S)根据其他属性为该待分类样本填充一个属性a值，然后进行分支处理。(F)在决策树中属性a节点的分支上，遍历属性a节点的所有分支，探索可能所有的分类结果，然后把这些分类结果结合起来一起考虑，按照概率决定一个分类。(H)待分类样本在到达属性a节点时就终止分类，然后根据此时a节点所覆盖的叶子节点类别状况为其分配一个发生概率最高的类。
3.4 推理规则
C4.5决策树能够根据决策树生成一系列规则集,我们可以把一颗决策树看成一系列规则的组合。一个规则对应着从根节点到叶子节点的路径，该规则的条件是路径上的条件，结果是叶子节点的类别。C4.5首先根据决策树的每个叶子节点生成一个规则集，对于规则集中的每条规则，算法利用“爬山”搜索来尝试是否有条件可以移除，由于移除一个条件和剪枝一个内部节点本质上是一样的，因此前面提到的悲观剪枝算法也被用在这里进行规则简化。MDL准则在这里也可以用来衡量对规则进行编码的信息量和对潜在的规则进行排序。简化后的规则数目要远远小于决策树的叶子节点数。根据简化后的规则集是无法重构原来的决策树的。规则集相比决策树而言更具有可操作性，因此在很多情况下我们需要从决策树中推理出规则集。C4.5有个缺点就是如果数据集增大了一点，那么学习时间会有一个迅速地增长。
4 可用的C4.5软件包
C4.5决策树算法如此
C4.5的原始实现可以从昆兰教授的个人网页http://www.rulequest.com/Personal/中得到，但这是c语言版本，而且这个版本不是免费的，你必须遵循他的商业许可证要求。开源的MLC++和Weka都有对C4.5的实现，你可以参考。另外也有一些商业版本的实现可供使用，比如ODBCMINE。
C4.5是一种早期的机器学习算法，在工业界也被广泛使用。
参考文献
[1]http://zh.wikipedia.org/zh-cn/二项式分布
[2]http://wenku.baidu.com/view/382a9c2558fb770bf78a5560.html
[3]The top ten algorithms in data mining
1.3、C4.5算法
C4.5，是机器学习算法中的另一个分类决策树算法，它是决策树(决策树也就是做决策的节点间的组织方式像一棵树，其实是一个倒树)核心算法，也是上文1.2节所介绍的ID3的改进算法，所以基本上了解了一半决策树构造方法就能构造它。
决策树构造方法其实就是每次选择一个好的特征以及分裂点作为当前节点的分类条件。
既然说C4.5算法是ID3的改进算法，那么C4.5相比于ID3改进的地方有哪些呢？：
- 用信息增益率来选择属性。ID3选择属性用的是子树的信息增益，这里可以用很多方法来定义信息，ID3使用的是熵(entropy，熵是一种不纯度度量准则),也就是熵的变化值，而C4.5用的是信息增益率。对，区别就在于一个是信息增益，一个是信息增益率。
- 在树构造过程中进行剪枝，在构造决策树的时候，那些挂着几个元素的节点，不考虑最好，不然容易导致overfitting。
- 对非离散数据也能处理。
- 能够对不完整数据进行处理
针对上述第一点，解释下：一般来说率就是用来取平衡用的，就像方差起的作用差不多，比如有两个跑步的人，一个起点是10m/s的人、其10s后为20m/s；另一个人起速是1m/s、其1s后为2m/s。如果紧紧算差值那么两个差距就很大了，如果使用速度增加率(加速度，即都是为1m/s^2)来衡量，2个人就是一样的加速度。因此，C4.5克服了ID3用信息增益选择属性时偏向选择取值多的属性的不足。
C4.5算法之信息增益率
OK，既然上文中提到C4.5用的是信息增益率，那增益率的具体是如何定义的呢？：
是的，在这里，C4.5算法不再是通过信息增益来选择决策属性。一个可以选择的度量标准是增益比率gain ratio（Quinlan 1986）。增益比率度量是用前面的增益度量Gain(S，A)和分裂信息度量SplitInformation(S，A)来共同定义的，如下所示：
其中，分裂信息度量被定义为( 分裂信息用来衡量属性分裂数据的广度和均匀)：
其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。注意分裂信息实际上就是S关于属性A的各值的熵。这与我们前面对熵的使用不同，在那里我们只考虑S关于学习到的树要预测的目标属性的值的熵。
请注意，分裂信息项阻碍选择值为均匀分布的属性。例如，考虑一个含有n个样例的集合被属性A彻底分割（译注：分成n组，即一个样例一组）。这时分裂信息的值为log2n。相反，一个布尔属性B分割同样的n个实例，如果恰好平分两半，那么分裂信息是1。如果属性A和B产生同样的信息增益，那么根据增益比率度量，明显B会得分更高。
使用增益比率代替增益来选择属性产生的一个实际问题是，当某个Si接近S（|Si|»|S|）时分母可能为0或非常小。如果某个属性对于S的所有样例有几乎同样的值，这时要么导致增益比率未定义，要么是增益比率非常大。为了避免选择这种属性，我们可以采用这样一些启发式规则，比如先计算每个属性的增益，然后仅对那些增益高过平均值的属性应用增益比率测试（Quinlan 1986）。
除了信息增益，Lopez de Mantaras（1991）介绍了另一种直接针对上述问题而设计的度量，它是基于距离的（distance-based）。这个度量标准基于所定义的一个数据划分间的距离尺度。具体更多请参看：Tom M.Mitchhell所著的机器学习之3.7.3节。
1.3.2、C4.5算法构造决策树的过程
- Function C4.5(R:包含连续属性的无类别属性集合,C:类别属性,S:训练集)
- Begin
- If S为空,返回一个值为Failure的单个节点;
- If S是由相同类别属性值的记录组成,
- 返回一个带有该值的单个节点;
- If R为空,则返回一个单节点,其值为在S的记录中找出的频率最高的类别属性值;
- [注意未出现错误则意味着是不适合分类的记录]；
- For 所有的属性R(Ri) Do
- If 属性Ri为连续属性，则
- Begin
- 将Ri的最小值赋给A1：
- 将Rm的最大值赋给Am；
- For j From 2 To m-1 Do Aj=A1+j*(A1Am)/m;
- 将Ri点的基于{< =Aj,>Aj}的最大信息增益属性(Ri,S)赋给A；
- End；
- 将R中属性之间具有最大信息增益的属性(D,S)赋给D;
- 将属性D的值赋给{dj/j=1,2...m}；
- 将分别由对应于D的值为dj的记录组成的S的子集赋给{sj/j=1,2...m};
- 返回一棵树，其根标记为D;树枝标记为d1,d2...dm;
- 再分别构造以下树:
- C4.5(R-{D},C,S1),C4.5(R-{D},C,S2)...C4.5(R-{D},C,Sm);
- End C4.5
1.3.3、C4.5算法实现中的几个关键步骤
在上文中，我们已经知道了决策树学习C4.5算法中4个重要概念的表达，如下：
- double C4_5::entropy(int *attrClassCount, int classNum, int allNum){
- double iEntropy = 0.0;
- for(int i = 0; i < classNum; i++){
- double temp = ((double)attrClassCount[i]) / allNum;
- if(temp != 0.0)
- iEntropy -= temp * (log(temp) / log(2.0));
- }
- return iEntropy;
- }
- double C4_5::gainRatio(int classNum, vector<int *> attriCount, double pEntropy){
- int* attriNum = new int[attriCount.size()];
- int allNum = 0;
- for(int i = 0; i < (int)attriCount.size(); i++){
- attriNum[i] = 0;
- for(int j = 0; j < classNum; j++){
- attriNum[i] += attriCount[i][j];
- allNum += attriCount[i][j];
- }
- }
- double gain = 0.0;
- double splitInfo = 0.0;
- for(int i = 0; i < (int)attriCount.size(); i++){
- gain -= ((double)attriNum[i]) / allNum * entropy(attriCount[i], classNum, attriNum[i]);
- splitInfo -= ((double)attriNum[i]) / allNum * (log(((double)attriNum[i])/allNum) / log(2.0));
- }
- gain += pEntropy;
- delete[] attriNum;
- return (gain / splitInfo);
- }
- int C4_5::chooseAttribute(vector<int> attrIndex, vector<int *>* sampleCount){
- int bestIndex = 0;
- double maxGainRatio = 0.0;
- int classNum = (int)(decisions[attrIndex[(int)attrIndex.size()-1]]).size();//number of class
- //computer the class entropy
- int* temp = new int[classNum];
- int allNum = 0;
- for(int i = 0; i < classNum; i++){
- temp[i] = sampleCount[(int)attrIndex.size()-1][i][i];
- allNum += temp[i];
- }
- double pEntropy = entropy(temp, classNum, allNum);
- delete[] temp;
- //computer gain ratio for every attribute
- for(int i = 0; i < (int)attrIndex.size()-1; i++){
- double gainR = gainRatio(classNum, sampleCount[i], pEntropy);
- if(gainR > maxGainRatio){
- bestIndex = i;
- maxGainRatio = gainR;
- }
- }
- return bestIndex;
- }
- form Wind：决策树适用于特征取值离散的情况，连续的特征一般也要处理成离散的(而很多文章没有表达出决策树的关键特征or概念)。实际应用中，决策树overfitting比较的严重，一般要做boosting。分类器的性能上不去，很主要的原因在于特征的鉴别性不足，而不是分类器的好坏，好的特征才有好的分类效果，分类器只是弱相关。
- 那如何提高 特征的鉴别性呢？一是设计特征时尽量引入domain knowledge，二是对提取出来的特征做选择、变换和再学习，这一点是机器学习算法不管的部分。
***********************
Decision Tree：CART、剪枝
决策树的重要性和入门可以参考前面两篇文章，尤其是入门的ID3算法：
http://isilic.iteye.com/blog/1841339、http://isilic.iteye.com/blog/1844097
Classification And Regression Tree(CART)也是决策树的一种，并且是非常重要的决策树。除去上文提到的C4.5外，CART算法也在Top Ten Machine Learning Algorithm中，可见决策树的重要性和CART算法的重要性。
CART的特性主要有下面三个，其实这些特性都不完全算是CART的特性，只是在CART算法中使用，并且作为算法的重要基础：
1：二分(Binary Split)：在每次判断过程中，都是对观察变量进行二分。
2：单变量分割(Split Based on One Variable)：每次最优划分都是针对单个变量。
3：剪枝策略：CART算法的关键点，也是整个Tree-Based算法的关键步骤。
CART能处理Classification Tree和Regression Tree，在建树过程中有不一样的地方，我们分别来看下。
我们先看Classification Tree的建树过程：
ID3, C4.5算法是利用熵理论和信息增益(率)来决定属性分割策略；CART则是利用Gini Index(GINI 指数)来定义衡量划分的好坏。和熵类似，数据内包含的类别越杂乱，GINI指数就越大，有没有感觉跟熵的概念类似。下面我们来学习下Gini Index的内容：
其中Pj是类j在T中的相对频率，当类j在T中是倾斜时，gini(T)才会最小。
比较熵理论和gini指数，让T中各类别出现的概率一致时，熵最大，Gini指数也是最大，但是两者的逼近速度是不一样的，从下图中可以看出来：
其中MisClassification Rate也是一种衡量，感兴趣的同学可以自行学习下。
衡量出某个属性的Gini指数后，可以得到Gini Split数据如下：
这个有没有和信息增益相似，这个可以称为是Gini信息增益，在CART中，选择其中最小的Gini信息增益作为结点划分决策树。
对于CART，i=2，可以得到在Binary Split情况下的Gini信息增益：
在weka中有信息增益weka.attributeSelection.InfoGainAttributeEval和信息增益率 weka.attributeSelection.GainRatioAttributeEval 的实现，可以看下实现原理。
Regression Tree的建树过程。
对于回归树，没有分类数据，只有根据观察数据得出的值，注意观察值取值是连续，在这种情况下Classification Tree的最优划分规则就无能为力。
在这种情况下，回归树可以使用 最小剩余方差(Squared Residuals Minimization)来决定Regression Tree的最优划分，该划分准则是期望划分之后的子树误差方差最小：
决策树停止生长的条件，这个可以看做是预剪枝过程：
树不能无限增长，我们可以设定条件，当树达到某个停止条件时，停止树增长，常用的停止条件（Stopping Criteria）有如下几个：
- 1：子树上的样本数据都归属于同一个类别
- 2：达到最大数深度(Maximum Tree Depth)
- 3：子树节点的样本数量要少于某个门限值，或者小于一定的比例
- 4：子树节点再按照最优划分标准切分，其子树的样本数量小于某个门限值，或者小于一定的比例值
- 5：最优划分(Split)标增益小于某个门限值，如误差值等
这些方法都可以让树提前停止增长，防止树无限制生成，避免一定程度上的过拟合。
剪枝理论，决策树的剪枝在上一节中没有仔细讲，趁这个机会学习了剪枝的基础理论，这里会详细学习。
决策树为什么(WHY)要剪枝？原因是避免决策树过拟合(Overfitting)样本。前面的算法生成的决策树非常详细并且庞大，每个属性都被详细地加以考虑，决策树的树叶节点所覆盖的训练样本都是“纯”的。因此用这个决策树来对训练样本进行分类的话，你会发现对于训练样本而言，这个树表现完好，误差率极低且能够正确得对训练样本集中的样本进行分类。训练样本中的错误数据也会被决策树学习，成为决策树的部分，但是对于测试数据的表现就没有想象的那么好，或者极差，这就是所谓的过拟合(Overfitting)问题。Quinlan教授试验，在数据集中，过拟合的决策树的错误率比经过简化的决策树的错误率要高。
现在问题就在于，如何(HOW)在原生的过拟合决策树的基础上，生成简化版的决策树？可以通过剪枝的方法来简化过拟合的决策树。剪枝可以分为两种：预剪枝(Pre-Pruning)和后剪枝(Post-Pruning),下面我们来详细学习下这两种方法：
PrePrune：预剪枝，及早的停止树增长，方法可以参考见上面树停止增长的方法。
PostPrune：后剪枝，在已生成过拟合决策树上进行剪枝，可以得到简化版的剪枝决策树。
其实剪枝的准则是如何确定决策树的规模，可以参考的剪枝思路有以下几个：
1：使用训练集合(Training Set）和验证集合(Validation Set)，来评估剪枝方法在修剪结点上的效用
2：使用所有的训练集合进行训练，但是用统计测试来估计修剪特定结点是否会改善训练集合外的数据的评估性能，如使用Chi-Square（Quinlan，1986）测试来进一步扩展结点是否能改善整个分类数据的性能，还是仅仅改善了当前训练集合数据上的性能。
3：使用明确的标准来衡量训练样例和决策树的复杂度，当编码长度最小时，停止树增长，如MDL(Minimum Description Length)准则。
我们先看下使用思路一来解决问题的集中后剪枝方法：
Reduced-Error Pruning(REP,错误率降低剪枝）
该剪枝方法考虑将书上的每个节点作为修剪的候选对象，决定是否修剪这个结点有如下步骤组成：
1：删除以此结点为根的子树
2：使其成为叶子结点
3：赋予该结点关联的训练数据的最常见分类
4：当修剪后的树对于验证集合的性能不会比原来的树差时，才真正删除该结点
因为训练集合的过拟合，使得验证集合数据能够对其进行修正，反复进行上面的操作，从底向上的处理结点，删除那些能够最大限度的提高验证集合的精度的结点，直到进一步修剪有害为止(有害是指修剪会减低验证集合的精度)
REP是最简单的后剪枝方法之一，不过在数据量比较少的情况下，REP方法趋于过拟合而较少使用。这是因为训练数据集合中的特性在剪枝过程中被忽略，所以在验证数据集合比训练数据集合小的多时，要注意这个问题。
尽管REP有这个缺点，不过REP仍然作为一种基准来评价其它剪枝算法的性能。它对于两阶段决策树学习方法的优点和缺点提供了了一个很好的学习思路。由于验证集合没有参与决策树的创建，所以用REP剪枝后的决策树对于测试样例的偏差要好很多，能够解决一定程度的过拟合问题。
Pessimistic Error Pruning(PEP，悲观剪枝）
先计算规则在它应用的训练样例上的精度，然后假定此估计精度为二项式分布，并计算它的标准差。对于给定的置信区间，采用下界估计作为规则性能的度量。这样做的结果，是对于大的数据集合，该剪枝策略能够非常接近观察精度，随着数据集合的减小，离观察精度越来越远。该剪枝方法尽管不是统计有效的，但是在实践中有效。
PEP为了提高对测试集合的预测可靠性，PEP对误差估计增加了连续性校正(Continuity Correction)。PEP方法认为，如果：
成立，则Tt应该被剪枝，上式中：
其中，e(t)为结点t出的误差；i为覆盖Tt的叶子结点；Nt为子树Tt的叶子树；n(t)为在结点t处的训练集合数量。PEP采用自顶向下的方式，如果某个非叶子结点符合上面的不等式，就裁剪掉该叶子结点。该算法被认为是当前决策树后剪枝算法中经度比较高的算法之一，但是饿存在有缺陷。首先，PEP算法是唯一使用Top-Down剪枝策略，这种策略会导致与先剪枝出现同样的问题，将该结点的某子节点不需要被剪枝时被剪掉；另外PEP方法会有剪枝失败的情况出现。
虽然PEP方法存在一些局限性，但是在实际应用中表现出了较高的精度,。两外PEP方法不需要分离训练集合和验证集合，对于数据量比较少的情况比较有利。再者其剪枝策略比其它方法相比效率更高，速度更快。因为在剪枝过程中，树中的每颗子树最多需要访问一次，在最坏的情况下，它的计算时间复杂度也只和非剪枝树的非叶子节点数目成线性关系。
可能有同学会对上面的那个不等式有疑问，可以参考这篇文章http://blog.sina.com.cn/s/blog_68ffc7a40100urn3.html 中关于PEP剪枝部分内容。PEP方法实际上是将结点误差数目看做二项式分布，根据期望和方差得到的结果。
Cost-Complexity Pruning(CCP、代价复杂度)
CCP方法包含两个步骤：
1：从原始决策树T0开始生成一个子树序列{T0、T1、T2、...、Tn},其中Ti+1是从Ti总产生，Tn为根节点
2：从子树序列中，根据树的真实误差估计选择最佳决策树。
在步骤一中，生成子树序列{T0、T1、T2、...、Tn}的基本思想是从T0开始，裁剪Ti中关于训练数据集合误差增加最小的分支来得到Ti+1。实际上当一棵树T在结点t出剪枝时，它的误差增加直观上认为是:
其中R(t)为在结点t的子树被裁剪后结点t的误差，R(Tt)为在结点t的子树没被裁剪时子树T的误差。不过剪枝后T的叶子树减少了|L(Ti)|-1，其中|L(Ti)|为子树Ti的叶子树，也就是说T的复杂性降低。因此考虑到树的复杂性因素，树分支被裁剪后误差增加率可以由下式决定：
Ti+1就是选择Ti中具有最小\alpha值所对应的剪枝树
如何从第一步骤产生的子树序列{T0、T1、T2、...、Tn}中选择出最佳决策树是CCP方法的第二步骤的关键。通常可以采用V-交叉验证(V-fold Cross-Validation)和基于独立剪枝数据集两种方法，这两种方法可以参考(Classification And Regression Trees,Breiman et.al)。当使用基于独立数据集剪枝时，和REP方法相比，CCP选择出来的最有决策树，不是从原始决策树T的所有可能子树中得到，所以有可能会找到到最有决策树。
其它如Minimum Error Pruning(MEP)，Critical Value Pruning(CVP)，Optimal Pruning(OPP)，Cost-Sensitive Decision Tree Pruning(CSDTP)等方法，这些剪枝方法各有利弊，关注不同的优化点，感兴趣的同学可以学习下。
剪枝过程特别重要，所以在最优决策树生成过程中占有重要地位。有研究表明，剪枝过程的重要性要比树生成过程更为重要，对于不同的划分标准生成的最大树(Maximum Tree)，在剪枝之后都能够保留最重要的属性划分，差别不大。反而是剪枝方法对于最优树的生成更为关键。重点理解这些剪枝方法的理论，对于最终最优树的生成是有好处的，其中上篇文章http://isilic.iteye.com/blog/1844097中C4.5使用了PEP剪枝方法，本文的CART使用了CCP的剪枝方法，实际上，不应该对于算法使用的剪枝方法过于追根究底，而是应该对于剪枝过程理解透彻，对于在何种场景下对于不同的数据类型使用何种的剪枝方法能够获得最优树的选择，才是真正理解了剪枝的理论和重要性。
下面再回到CART算法，看下算法的优点：
1：没有分布假设、没有数据同质性(Homogeneity)要求
2：观测值属性可以是分类、离散、连续的混合。
4：对异常值(Outlier)值不敏感，异常值一般会被处理掉
5：在面对缺失值、变量多等问题时，CART显得给长稳健(ROBUST)
缺点：
1：非基于概率模型，很难对决策树的结果的准确程度做度量
CART算法的内容就到这里，再扩充下Decision Tree算法的内容。上面的这些决策树算法都是单变量(Univariate)算法，实际上还有多变量(MultiVariate)算法，只是使用比较少。在Machine Learning In Action第九章中有关于Tree-Based Regression，是讲解CART中Regression树的内容。尤其是在文章中间提到了多变量回归树算法，每次的判定点有两个变量组成，对于本文的内容是个非常好的扩充，可以学习下。另外要提一下的是该章节中讲解的CART生成比较简单，尤其是生成最大树的方法；不过树生成和数剪枝(包括预剪枝和后剪枝)都有体现，算是分不错的代码文档；感兴趣的可以直接在这份代码上修改。
后面附加了份关于决策树的概论内容综述，地址参见：http://www.ise.bgu.ac.il/faculty/liorr/hbchap9.pdf 。内容比较全，包括划分标准、剪枝方法，不过不够深入，只有公式和简单的介绍，如果有基础的话话，倒是份不错的文档。如果不能观看的话，文后有附件。
另外在百度文库上有个PPT不错：http://wenku.baidu.com/view/415c3cc19ec3d5bbfd0a7464.html，供参考。
其实本文的重点是剪枝的内容，除去这点，CART算法使用的GINI指数内容也是本文的重点。
本文内容结束。
- hbchap9.pdf (424.6 KB)
- 下载次数: 2
- 查看图片附件
***
Decision Tree：Analysis
大家有没有玩过猜猜看(Twenty Questions)的游戏？我在心里想一件物体，你可以用一些问题来确定我心里想的这个物体；如是不是植物？是否会飞？能游泳不？当你问完这些问题后，你就能得到这个物体的特征，然后猜出我心里想象的那个物体，看是否正确。
这个游戏很简单，但是蕴含的思想却是质朴的。每个问题都会将范围减少，直到特征显现，内蕴的思想就是Decision Tree算法。判定树(Decision Tree)算法是机器学习中很重要的一种算法，有文章声称该算法在ML学习中最为常用的算法，你不需要明白高深的知识就能明白算法的运行原理。
Decision Tree包括以下几个部分：
- Root：根节点，Decision Tree使用了树的概念，必然有Root属性。
- Decision Node：判定节点，该节点的数据会继续根据数据属性继续进行判定。
- Branch：从Decision Node迭代生成的子树是子树根节点的一个属性判断
- End Node：也称为Leaf Node，该节点实际上是做出决定的节点，对于样本属性的判断到Leaf Node结束。
Decision Tree分类：
Classification Tree：测试数据经过Classification Tree处理后，看结果归属于那个类别(Class)。
Regression Tree：如果测试数据的输出是数值类型，可以考虑使用Regression Tree。
CART(Classification And Regression Tree)s算法是对上面两种算法的术语涵盖。用来回归的树(Regression Tree)和用来分类的树(classification Tree)具有一定的相似性，不过其不同之处在于决定分裂(Split)的过程。
使用某些技术(Ensemble Methods)，可以构建多个Decision Tree：
Bagging Decision Tree：创建多个Decision Tree，通过替换训练集合，得到多个Decision Tree，最终得到一致的结果。
Random Forest Classification Decision Tree：使用多个Decision Tree，提升分类的准确率。
Boosted Trees：可以使用于回归(Regression)和分类(Classification)的问题。
Rotation Forest：Decision Tree生成是从训练集合特征属性中随机选取，使用PCA分析方法来构建Decision Tree。
Gini Impurity
该Gini度量是指随机选择集合中的元素，根据集合中label的分布将该元素赋予分类，该元素分类错误的几率。Gini度量在CART算法中使用，其定义如下：
其中i为label标签，fi为label为i标签的比例(Fraction)
Information Gain
这个是比较常见的信息度量，在Information Theory中经常使用，基于熵(entropy)的概念。在ID3、C4.5、C5.0中使用。其定义如下：
i为label标签，fi为label标签的比例，和上面的定义一致。Information Gain的定义如下：
Entropy和Information Gain的定义还会在后面章节里用到，确保自己正确理解了Information Gain的定义。 本文最后会有个教程，帮助大家学习下Information Gain的概念。
Decision Tree的优点和缺点：
1：易于理解和解释，简单解释就能明白Decision Tree的模型和运行原理，对于结果也比较容易解释。
2：数据预处理少，其它算法需要处理Data Normalization、Dummy Variable、Blank Value都需要进行预处理。
3：能够处理数值数据和分类数据，能够使用Decision Tree和Regression Tree就是例证。
4：使用白盒(White Box)模型，使用白盒模型能够在给定测试数据下解释测试结果分类，NN(Neural Network)分类就难以解释，至少没有Decision Tree模型明晰。
5：易于使用统计数据验证模型，能够解释模型的可用性和可信赖度
6：健壮，数据假设比较少，该模型仅仅依赖于观察到的数据，归于数据生成模型假设比较少。
7：在大数据量情况下也能很快给出结果，根据Decision Tree抽取出来的规则能够很快的运用于测试数据，运行快速。
缺点：
1：最优Decision Tree是NP难题，所以使用的Decision-Tree算法都是基于启发式(Heuristic)算法，如Greedy Algorithm等，在每个节点判断都是根据局部最优解来进行操作。启发式算法不能保证返回全局最优的Decision Tree。
2：容易产生过于复杂的树，不能很好地获得数据的通用模型，这个实际上是被称为是Overfitting，剪枝技术能够很好的避免这个问题。
3：Decision Tree的表示能力有限，只能表示有限的数据操作，如XOR、Parity、Multiplexer等操作就不易表示；导致Decision Tree变得特别大，解决方法可以使用改变问题域的表示(Propositionalisation)，或者使用更加复杂的表示方法，如Statistical Relational Learning、Inductive Logic Programming等。
4：对于包含分类变量(Categorical Variable)的数据，使用Information Gain分裂会造成较大的偏差
Extension：
Decision Tree使用And或者是Conjunction来在Decision Node进行判断，逐步得到结果；Decision Graph则是使用Or或者Disjunction来连接路径(判断条件)。在Decision Graph中，使用MML(Minimum Message length)来对Path进行处理，更细节的内容请自行查找。
关于Decision Tree的实现比较多，其中Weka中有一部分Decision Tree的经典算法实现，大家可以将weka的源码下载下来，仔细阅读下。
参考文献：
http://www.comp.lancs.ac.uk/~kc/Lecturing/csc355/DecisionTrees_given.pdf
***
Decision Tree：ID3、C4.5
ID3(Iterative Dichotomiser 3)算法是判定树算法(Decision Tree Learning)的典型代表算法，由Ross Quinlan在1975年提出。ID3是作为C4.5的先驱，在Machine Learning和Natural Language Processing中使用广泛。该分类算法的核心是Entropy理论，属于数学的范畴。Entropy Theory是信息论中的名词，在上篇文章中http://isilic.iteye.com/blog/1841339有介绍，不过关于信息熵还有一些更深一些的东西。
信息熵
信息熵是指：一组数据所包含的信息量，使用概率来度量。数据包含的信息越有序，所包含的信息越低；数据包含的信息越杂，包含的信息越高。例如在极端情况下，如果数据中的信息都是0，或者都是1，那么熵值为0，因为你从这些数据中得不到任何信息，或者说这组数据给出的信息是确定的。如果数据时均匀分布，那么他的熵最大，因为你根据数据不能知晓那种情况发生的可能性比较大。
计算熵的公式为：
熵值和概率的关系如下，这个是二值情况下的概率与熵值关系，其中n=2：
实际上，信息熵表示的是信息的不确定性。当概率相同时，不确定性越大，因为所有的信息概率相同，你不能确定哪个信息出现的可能性更大；当某类别发生的概率为0或者1时，给出的结果是确定的(出现或者不出现、发生或者不发生)。这样的解释会不会更清楚点。
Information Gain(IG)，信息增益和信息熵描述的信息是一致的；描述的是对于数据集合S，将其按照其属性A切分后，获得的信息增益值。注意IG描述的是信息的增益值，当不确定性越大时，信息增益值应该是越小，反之亦然，是负相关的关系。信息增益的公式如下：
在ID3中，使用信息增益(IG)或者熵(Entropy)值来确定使用哪个属性进行判定属性，可以说是ID3算法的关键和精髓所在。ID3算法的伪码如下：
ID3算法的原理还是比较简单的，其理论基础是Entropy理论和Information Gain理论，只要深入理解了这个内容，ID3算法就不是问题。其实Machine Learning的基础是统计、概率、几何知识的考量，数学基础好的话，会在学习过程中感觉轻松些。
在Machine Learning in Action中有个章节是介绍ID3算法的，并且有完整的实现。我将代码拿过来，感兴趣的可以结合理论学习一下。
- from math import log
- import operator
- def createDataSet():
- dataSet = [[1, 1, 'yes'],
- [1, 1, 'yes'],
- [1, 0, 'no'],
- [0, 1, 'no'],
- [0, 1, 'no']]
- labels = ['no surfacing','flippers']
- #change to discrete values
- return dataSet, labels
- def calcShannonEnt(dataSet):
- numEntries = len(dataSet)
- labelCounts = {}
- for featVec in dataSet: #the the number of unique elements and their occurance
- currentLabel = featVec[-1]
- if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
- labelCounts[currentLabel] += 1
- shannonEnt = 0.0
- for key in labelCounts:
- prob = float(labelCounts[key])/numEntries
- shannonEnt -= prob * log(prob,2) #log base 2
- return shannonEnt
- def splitDataSet(dataSet, axis, value):
- retDataSet = []
- for featVec in dataSet:
- if featVec[axis] == value:
- reducedFeatVec = featVec[:axis] #chop out axis used for splitting
- reducedFeatVec.extend(featVec[axis+1:])
- retDataSet.append(reducedFeatVec)
- return retDataSet
- def chooseBestFeatureToSplit(dataSet):
- numFeatures = len(dataSet[0]) - 1 #the last column is used for the labels
- baseEntropy = calcShannonEnt(dataSet)
- bestInfoGain = 0.0; bestFeature = -1
- for i in range(numFeatures): #iterate over all the features
- featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
- uniqueVals = set(featList) #get a set of unique values
- newEntropy = 0.0
- for value in uniqueVals:
- subDataSet = splitDataSet(dataSet, i, value)
- prob = len(subDataSet)/float(len(dataSet))
- newEntropy += prob * calcShannonEnt(subDataSet)
- infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy
- if (infoGain > bestInfoGain): #compare this to the best gain so far
- bestInfoGain = infoGain #if better than current best, set to best
- bestFeature = i
- return bestFeature #returns an integer
- def majorityCnt(classList):
- classCount={}
- for vote in classList:
- if vote not in classCount.keys(): classCount[vote] = 0
- classCount[vote] += 1
- sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
- return sortedClassCount[0][0]
- def createTree(dataSet,labels):
- classList = [example[-1] for example in dataSet]
- if classList.count(classList[0]) == len(classList):
- return classList[0]#stop splitting when all of the classes are equal
- if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
- return majorityCnt(classList)
- bestFeat = chooseBestFeatureToSplit(dataSet)
- bestFeatLabel = labels[bestFeat]
- myTree = {bestFeatLabel:{}}
- del(labels[bestFeat])
- featValues = [example[bestFeat] for example in dataSet]
- uniqueVals = set(featValues)
- for value in uniqueVals:
- subLabels = labels[:] #copy all of labels, so trees don't mess up existing labels
- myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
- return myTree
- def classify(inputTree,featLabels,testVec):
- firstStr = inputTree.keys()[0]
- secondDict = inputTree[firstStr]
- featIndex = featLabels.index(firstStr)
- key = testVec[featIndex]
- valueOfFeat = secondDict[key]
- if isinstance(valueOfFeat, dict):
- classLabel = classify(valueOfFeat, featLabels, testVec)
- else: classLabel = valueOfFeat
- return classLabel
- def storeTree(inputTree,filename):
- import pickle
- fw = open(filename,'w')
- pickle.dump(inputTree,fw)
- fw.close()
- def grabTree(filename):
- import pickle
- fr = open(filename)
- return pickle.load(fr)
代码还算清晰，chooseBestFeatureToSplit和calcShannonEnt这两个方法是ID3算法的核心，请仔细阅读代码，确定自己真正理解了熵理论和信息增益理论。
ID3算法存在的缺点：
1：ID3算法在选择根节点和内部节点中的分支属性时，采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多是属性在有些情况下这类属性可能不会提供太多有价值的信息。
2：ID3算法只能对描述属性为离散型属性的数据集构造决策树
ID3算法的局限是它的属性只能取离散值,为了使决策树能应用于连续属性值情况，Quinlan给出了ID3的一个扩展算法：即C4.5算法。C4.5算法是ID3的改进，其中离散属性值的选择依据同ID3；它对于实值变量的处理采用多重分支。C4.5算法能实现基于规则的剪枝。因为算法生成的每个叶子都和一条规则相关联，这个规则可以从树的根节点直到叶子节点的路径上以逻辑合取式的形式读出。
C4.5算法之所以是最常用的决策树算法，是因为它继承了ID3算法的所有优点并对ID3算的进行了改进和补充。C4.5算法采用信息增益率作为选择分支属性的标准，并克服了ID3算法中信息增益选择属性时偏向选择取值多的属性的不足，并能够完成对连续属性离散化是处理；还能够对不完整数据进行处理。C4.5算法属于基于信息论Information Theory的方法，以信息论为基础，以信息熵和信息增益度为衡量标准，从而实现对数据的归纳和分类。
C4.5算法主要做出了以下方面的改进
1：可以处理连续数值型属性
对于离散值，C4.5和ID3的处理方法相同，对于某个属性的值连续时，假设这这个节点上的数据集合样本为total，C4.5算法进行如下处理：
- 将样本数据该属性A上的具体数值按照升序排列，得到属性序列值：{A1,A2,A3,...,Atotal}
- 在上一步生成的序列值中生成total-1个分割点。第i个分割点的取值为Ai和Ai+1的均值，每个分割点都将属性序列划分为两个子集。
- 计算每个分割点的信息增益(Information Gain),得到total-1个信息增益。
- 对分裂点的信息增益进行修正：减去log2(N-1)/|D|，其中N为可能的分裂点个数，D为数据集合大小。
- 选择修正后的信息增益值最大的分类点作为该属性的最佳分类点
- 计算最佳分裂点的信息增益率(Gain Ratio)作为该属性的Gain Ratio
- 选择Gain Ratio最大的属性作为分类属性。
其中第4、5步骤Quinlan在93年的的算法中没有体现，在96年发表文章对该算法进行改进，改进的论文可以参考这里：http://www.cs.cmu.edu/afs/cs/project/jair/pub/volume4/quinlan96a.pdf。
2：用信息增益率(Information Gain Ratio)来选择属性
克服了用信息增益来选择属性时偏向选择值多的属性的不足。信息增益率定义为：
其中Gain(S,A)和ID3算法中的信息增益计算相同，而SplitInfo(S,A)代表了按照属性A分裂样本集合S的广度和均匀性。
其中Si表示根据属性A分割S而成的样本子集。
3：后剪枝策略
Decision Tree很容易产生Overfitting，剪枝能够避免树高度无限制增长，避免过度拟合数据。剪枝算法比较复杂，我自己还没有学习清楚，希望大家能提供学习这个剪枝策略方法的建议。
4：缺失值处理
对于某些采样数据，可能会缺少属性值。在这种情况下，处理缺少属性值的通常做法是赋予该属性的常见值，或者属性均值。另外一种比较好的方法是为该属性的每个可能值赋予一个概率，即将该属性以概率形式赋值。例如给定Boolean属性B，已知采样数据有12个B=0和88个B=1实例，那么在赋值过程中，B属性的缺失值被赋值为B(0)=0.12、B(1)=0.88；所以属性B的缺失值以12%概率被分到False的分支，以88%概率被分到True的分支。这种处理的目的是计算信息增益，使得这种属性值缺失的样本也能处理。
我们看下C4.5算法的伪码：
- Function C4.5(R:包含连续属性的无类别属性集合,C:类别属性,S:训练集)
- Begin
- If S为空,返回一个值为Failure的单个节点;
- If S是由相同类别属性值的记录组成,
- 返回一个带有该值的单个节点;
- If R为空,则返回一个单节点,其值为在S的记录中找出的频率最高的类别属性值;
- [注意未出现错误则意味着是不适合分类的记录]；
- For 所有的属性R(Ri) Do
- If 属性Ri为连续属性，则
- Begin
- sort(Ri属性值)
- 将Ri的最小值赋给A1：
- 将Ri的最大值赋给Am；
- For j From 1 To m-1 Do Aj=(A1+Aj+1)/2;
- 将Ri点的基于Aj(1<=j<=m-1划分的最大信息增益属性(Ri,S)赋给A；
- End；
- 将R中属性之间具有最大信息增益的属性(D,S)赋给D;
- 将属性D的值赋给{dj/j=1,2...m}；
- 将分别由对应于D的值为dj的记录组成的S的子集赋给{sj/j=1,2...m};
- 返回一棵树，其根标记为D;树枝标记为d1,d2...dm;
- 再分别构造以下树:
- C4.5(R-{D},C,S1),C4.5(R-{D},C,S2)...C4.5(R-{D},C,Sm);
- End C4.5
该算法流程是我从网上移过来的，对于其中和本文描述不一致的地方做了修改。原文参考这里：http://blog.sina.com.cn/s/blog_73621a3201017g7k.html
C4.5的主要点在于对于ID3的改进，可以说上面提到的四点对于Decision Tree算法来说是非常关键的，理解了这几个改进点就算是掌握了C4.5算法的根本。
C4.5的缺点：
1：算法低效，在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效
2：内存受限，适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。
在weka开源软件中有个weka.classifiers.trees.J48实现了C4.5算法，可以结合该代码学习理论知识。
最后提示下C5.0算法，C5.0算法是在C4.5算法基础上的改进，wiki上表示该算法应该归属于商业应用，所以没有C4.5讨论广泛。相比较于C4.5，C5.0算法的改进点在于：
1：速度，C5.0有好几个数量级别上的速度提升
2：内存使用，比C4.5使用更加有效
3：生成Decision Tree更小(Occam's Razor)，能避免过度拟合
4：支持Boosting
5：支持权重，对于不同的样本赋予不同的权重值
6：Winnowing：支持自动去除没有帮助的属性
这个是作者的声明。尤其是前两点，刚好是克服了C4.5算法的劣势，是C4.5算法的巨大提升，算法源码在http://rulequest.com/download.html这里有下载，大家可以学习下作者声称的优势都是怎么实现的。在这里http://www.rulequest.com/see5-comparison.html有C5.0和C4.5的比较，大家也可以看下，从文章来看，C5.0确实是在很多方面都超过了C4.5。
本文关于Decision Tree的学习到此，本文介绍了最为简单和基础的ID3算法；随后学习了C4.5相比于ID3的优势及实现思路；最后比较了C5.0的改进；对于Decision Tree算法有了基本的认识，为后面学习Decision Tree算法提供了良好的基础。