Learning to learn by gradient descent by gradient descent - PyTorch实践
原创博文,转载请注明来源
https://senyang-ml.github.io/2018/12/17/learning_to_learn/
引言
“浪费75金币买控制守卫有什么用,还不是让人给拆了?我要攒钱!早晚憋出来我的灭世者的死亡之帽!”
Learning to learn,即学会学习,是每个人都具备的能力,具体指的是一种在学习的过程中去反思自己的学习行为来进一步提升学习能力的能力。这在日常生活中其实很常见,比如在通过一本书来学习某个陌生专业的领域知识时(如《机器学习》),面对大量的专业术语与陌生的公式符号,初学者很容易看不下去,而比较好的方法就是先浏览目录,掌握一些简单的概念(回归与分类啊,监督与无监督啊),并在按顺序的阅读过程学会“前瞻”与“回顾”,进行快速学习。又比如在早期接受教育的学习阶段,盲目的“题海战术”或死记硬背的“知识灌输”如果不加上恰当的反思和总结,往往会耗时耗力,最后达到的效果却一般,这是因为在接触新东西,掌握新技能时,是需要“技巧性”的。
从学习知识到学习策略的层面上,总会有“最强王者”在告诉我们,“钻石的操作、黄铜的意识”也许并不能取胜,要“战略上最佳,战术上谨慎”才能更快更好地进步。
这跟本文要讲的内容有什么关系呢?进入正题。
其实读者可以先回顾自己从初高中到大学甚至研究生的整个历程,是不是发现自己已经具备了“learning to learn”的能力?
Learning to learn
by gradient descent
by gradient descent
“通过梯度下降来学习如何通过梯度下降学习”
是否可以让优化器学会 “为了更好地得到,要先去舍弃” 这样的“策略”?
本博客结合具体实践来解读《Learning to learn by gradient descent by gradient descent》,这是一篇Meta-learning(元学习)领域的论文,发表在2016年的NIPS。类似“回文”结构的起名,让这篇论文变得有趣,是不是可以再套一层,“Learning to learn to learn by gradient descent by gradient descent by gradient descent”?再套一层?
首先别被论文题目给误导,它不是求梯度的梯度,这里不涉及到二阶导的任何操作,而是跟如何学会更好的优化有关,正确的断句方法为learning to (learn by gradient descent ) by gradient descent 。
第一次读完后,不禁惊叹作者巧妙的构思–使用LSTM(long short-term memory)优化器来替代传统优化器如(SGD,RMSProp,Adam等),然后使用梯度下降来优化优化器本身。
虽然明白了作者的出发点,但总感觉一些细节自己没有真正理解。然后就去看原作的代码实现,读起来也是很费劲。查阅了一些博客,但网上对这篇论文解读很少,停留于论文翻译理解上。再次揣摩论文后,打算做一些实验来理解。 在用PyTorch写代码的过程,才恍然大悟,作者的思路是如此简单巧妙,论文名字起的也很恰当,没在故弄玄虚,但是在实现的过程却费劲了周折!
如果想看最终版代码和结果,可以直接跳到文档的最后!!!
下面写的一些文字与代码主要站在我自身的角度,记录自己在学习研究这篇论文和代码过程中的所有历程,如何想的,遇到了什么错误,问题在哪里,我把自己理解领悟“learning to learn”这篇论文的过程剖析了一下,也意味着我自己也在“learning to learn”!为了展现自己的心路历程,我基本保留了所有的痕迹,这意味着有些代码不够整洁,不过文档的最后是最终简洁完整版。
提醒:看完整个文档需要大量的耐心 : )
我默认读者已经掌握了一些必要知识,也希望通过回顾这些经典研究给自己和一些读者带来切实的帮助和启发。
用Pytorch实现这篇论文想法其实很方便,但是论文作者来自DeepMind,他们用Tensorflow写的项目,读他们的代码你就会领教到最前沿的一线AI工程师们是如何进行工程实践的。
下面进入正题,我会按照最简单的思路,循序渐进地展开, <0…0>。
优化问题
经典的机器学习问题,包括当下的深度学习相关问题,大多可以被表达成一个目标函数的优化问题:
θ ∗ = arg min θ ∈ Θ f ( θ ) \theta ^{*}= \arg\min_{\theta\in \Theta }f\left ( \theta \right ) θ∗=argθ∈Θminf(θ)
一些优化方法可以求解上述问题,最常见的即梯度更新策略:
θ t + 1 = θ t − α t ∗ ∇ f ( θ t ) \theta_{t+1}=\theta_{t}-\alpha_{t}*\nabla f\left ( \theta_{t}\right ) θt+1=θt−αt∗∇f(θt)
早期的梯度下降会忽略梯度的二阶信息,而经典的优化技术通过加入曲率信息改变步长来纠正,比如Hessian矩阵的二阶偏导数。
Deep learning社区的壮大,演生出很多求解高维非凸的优化求解器,如
momentum[Nesterov, 1983, Tseng, 1998], Rprop [Riedmiller and Braun, 1993], Adagrad [Duchi et al., 2011], RMSprop [Tieleman and Hinton, 2012], and ADAM [Kingma and Ba, 2015].
目前用于大规模图像识别的模型往往使用卷积网络CNN通过定义一个代价函数来拟合数据与标签,其本质还是一个优化问题。
这里我们考虑一个简单的优化问题,比如求一个四次非凸函数的最小值点。对于更复杂的模型,下面的方法同样适用。
定义要优化的目标函数
import torch
import torch.nn as nn
DIM = 10
w = torch.empty(DIM)
torch.nn.init.uniform_(w,a=0.5,b=1.5)
def f(x): #定义要优化的函数,求x的最优解
x= w*(x-1)
return ((x+1)*(x+0.5)*x*(x-1)).sum()
定义常用的优化器如SGD, RMSProp, Adam。
SGD仅仅只是给梯度乘以一个学习率。
RMSProp的方法是:
E [ g 2 ] t = 0.9 E [ g 2 ] t − 1 + 0.1 g t 2 E[g^2]_t = 0.9 E[g^2]_{t-1} + 0.1 g^2_t E[g2]t=0.9E[g2]t−1+0.1gt2
θ t + 1 = θ t − η E [ g 2 ] t + ϵ g t \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t} θt+1=θt−E[g2]t+ϵηgt
当前时刻下,用当前梯度和历史梯度的平方加权和(越老的历史梯度,其权重越低)来重新调节学习率(如果历史梯度越低,“曲面更平坦”,那么学习率越大,梯度下降更“激进”一些,如果历史梯度越高,“曲面更陡峭”那么学习率越小,梯度下降更“谨慎”一些),来更快更好地朝着全局最优解收敛。
Adam是RMSProp的变体:
m t = β 1 m t − 1 + ( 1 − β 1 ) g t v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 mt=β1mt−1+(1−β1)gtvt=β2vt−1+(1−β2)gt2
m ^ t = m t 1 − β 1 t v ^ t = v t 1 − β 2 t \hat{m}_t = \dfrac{m_t}{1 - \beta^t_1} \\ \hat{v}_t = \dfrac{v_t}{1 - \beta^t_2} m^t=1−β1tmtv^t=1−β2tvt
θ t + 1 = θ t − η v ^ t + ϵ m ^ t \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t θt+1=θt−v^t+ϵηm^t
即通过估计当前梯度的一阶矩估计和二阶矩估计来代替,梯度和梯度的平方,然后更新策略和RMSProp一样。
def SGD(gradients, state, learning_rate=0.001):
return -gradients*learning_rate, state
def RMS(gradients, state, learning_rate=0.1, decay_rate=0.9):
if state is None:
state = torch.zeros(DIM)
state = decay_rate*state + (1-decay_rate)*torch.pow(gradients, 2)
update = -learning_rate*gradients / (torch.sqrt(state+1e-5))
return update, state
def Adam():
return torch.optim.Adam()
这里的Adam优化器直接用了Pytorch里定义的。然后我们通过优化器来求解极小值x,通过梯度下降的过程,我们期望的函数值是逐步下降的。
这是我们一般人为设计的学习策略,即逐步梯度下降法,以“每次都比上一次进步一些” 为原则进行学习!
接下来 构造优化算法
TRAINING_STEPS = 15
theta = torch.empty(DIM)
torch.nn.init.uniform_(theta,a=-1,b=1.0)
theta_init = torch.tensor(theta,dtype=torch.float32,requires_grad=True)
def learn(optimizee,unroll_train_steps,retain_graph_flag=False,reset_theta = False):
"""retain_graph_flag=False PyTorch 默认每次loss_backward后 释放动态图
# reset_theta = False 默认每次学习前 不随机初始化参数"""
if reset_theta == True:
theta_new = torch.empty(DIM)
torch.nn.init.uniform_(theta_new,a=-1,b=1.0)
theta_init_new = torch.tensor(theta,dtype=torch.float32,requires_grad=True)
x = theta_init_new
else:
x = theta_init
global_loss_graph = 0 #这个是为LSTM优化器求所有loss相加产生计算图准备的
state = None
x.requires_grad = True
if optimizee.__name__ !='Adam':
losses = []
for i in range(unroll_train_steps):
x.requires_grad = True
loss = f(x)
#global_loss_graph += (0.8*torch.log10(torch.Tensor([i]))+1)*loss
global_loss_graph += loss
#print(loss)
loss.backward(retain_graph=retain_graph_flag) # 默认为False,当优化LSTM设置为True
update, state = optimizee(x.grad, state)
losses.append(loss)
#这个操作 直接把x中包含的图给释放了,
x = x + update
x = x.detach_()
#这个操作 直接把x中包含的图给释放了,
#那传递给下次训练的x从子节点变成了叶节点,那么梯度就不能沿着这个路回传了,
#之前写这一步是因为这个子节点在下一次迭代不可以求导,那么应该用x.retain_grad()这个操作,
#然后不需要每次新的的开始给x.requires_grad = True
#x.retain_grad()
#print(x.retain_grad())
#print(x)
return losses ,global_loss_graph
else:
losses = []
x.requires_grad = True
optimizee= torch.optim.Adam( [x],lr=0.1 )
for i in range(unroll_train_steps):
optimizee.zero_grad()
loss = f(x)
global_loss_graph += loss
loss.backward(retain_graph=retain_graph_flag)
optimizee.step()
losses.append(loss.detach_())
#print(x)
return losses,global_loss_graph
对比不同优化器的优化效果
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
T = np.arange(TRAINING_STEPS)
for _ in range(1):
sgd_losses, sgd_sum_loss = learn(SGD,TRAINING_STEPS,reset_theta=True)
rms_losses, rms_sum_loss = learn(RMS,TRAINING_STEPS,reset_theta=True)
adam_losses, adam_sum_loss = learn(Adam,TRAINING_STEPS,reset_theta=True)
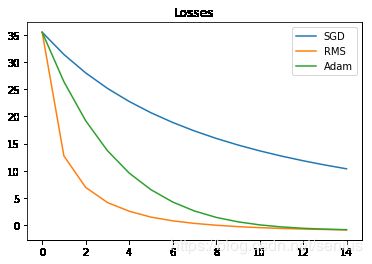
p1, = plt.plot(T, sgd_losses, label='SGD')
p2, = plt.plot(T, rms_losses, label='RMS')
p3, = plt.plot(T, adam_losses, label='Adam')
plt.legend(handles=[p1, p2, p3])
plt.title('Losses')
plt.show()
print("sum_loss:sgd={},rms={},adam={}".format(sgd_sum_loss,rms_sum_loss,adam_sum_loss ))
sum_loss:sgd=289.9213562011719,rms=60.56287384033203,adam=117.2123031616211
通过上述实验可以发现,这些优化器都可以发挥作用,似乎RMS表现更加优越一些,不过这并不代表RMS就比其他的好,可能这个优化问题还是较为简单,调整要优化的函数,可能就会看到不同的结果。
Meta-optimizer :从手工设计优化器迈步到自动设计优化器
上述这些优化器的更新策略是根据人的经验主观设计,要来解决一般的优化问题的。
No Free Lunch Theorems for Optimization [Wolpert and Macready, 1997] 表明组合优化设置下,没有一个算法可以绝对好过一个随机策略。这暗示,一般来讲,对于一个子问题,特殊化其优化方法是提升性能的唯一方法。
而针对一个特定的优化问题,也许一个特定的优化器能够更好的优化它,我们是否可以不根据人工设计,而是让优化器本身根据模型与数据,自适应地调节,这就涉及到了meta-learning
用一个可学习的梯度更新规则,替代手工设计的梯度更新规则
θ t + 1 = θ t + g t ( f ( θ t ) , ϕ ) \theta_{t+1}=\theta_{t}+g\textit{}_{t}\left (f\left ( \theta_{t}\right ),\phi \right) θt+1=θt+gt(f(θt),ϕ)
这里的 g ( ⋅ ) g(\cdot) g(⋅)代表其梯度更新规则函数,通过参数 ϕ \phi ϕ来确定,其输出为目标函数f当前迭代的更新梯度值, g g g函数通过RNN模型来表示,保持状态并动态迭代
假如一个优化器可以根据历史优化的经验来自身调解自己的优化策略,那么就一定程度上做到了自适应,这个不是说像Adam,momentum,RMSprop那样自适应地根据梯度调节学习率,(其梯度更新规则还是不变的),而是说自适应地改变其梯度更新规则,而Learning to learn 这篇论文就使用LSTM(RNN)优化器做到了这一点,毕竟RNN存在一个可以保存历史信息的隐状态,LSTM可以从一个历史的全局去适应这个特定的优化过程,做到论文提到的所谓的“CoordinateWise”,我的理解是:LSTM的参数对每个时刻节点都保持“聪明”,是一种“全局性的聪明”,适应每分每秒。
构建LSTM优化器
Layers = 2
Hidden_nums = 20
Input_DIM = DIM
Output_DIM = DIM
# "coordinate-wise" RNN
lstm=torch.nn.LSTM(Input_DIM,Hidden_nums ,Layers)
Linear = torch.nn.Linear(Hidden_nums,Output_DIM)
batchsize = 1
print(lstm)
def LSTM_Optimizee(gradients, state):
#LSTM的输入为梯度,pytorch要求torch.nn.lstm的输入为(1,batchsize,input_dim)
#原gradient.size()=torch.size[5] ->[1,1,5]
gradients = gradients.unsqueeze(0).unsqueeze(0)
if state is None:
state = (torch.zeros(Layers,batchsize,Hidden_nums),
torch.zeros(Layers,batchsize,Hidden_nums))
update, state = lstm(gradients, state) # 用optimizee_lstm代替 lstm
update = Linear(update)
# Squeeze to make it a single batch again.[1,1,5]->[5]
return update.squeeze().squeeze(), state
LSTM(10, 20, num_layers=2)
从上面LSTM优化器的设计来看,我们几乎没有加入任何先验的人为经验在里面,只是用了长短期记忆神经网络的架构
优化器本身的参数即LSTM的参数,这个优化器的参数代表了我们的更新策略,后面我们会学习这个参数,即学习用什么样的更新策略
对了如果你不太了解LSTM的话,我就放这个网站 http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 博客的几个图,它很好解释了什么是RNN和LSTM:
好了,看一下我们使用刚刚初始化的LSTM优化器后的优化结果
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
x = np.arange(TRAINING_STEPS)
for _ in range(1):
sgd_losses, sgd_sum_loss = learn(SGD,TRAINING_STEPS,reset_theta=True)
rms_losses, rms_sum_loss = learn(RMS,TRAINING_STEPS,reset_theta=True)
adam_losses, adam_sum_loss = learn(Adam,TRAINING_STEPS,reset_theta=True)
lstm_losses,lstm_sum_loss = learn(LSTM_Optimizee,TRAINING_STEPS,reset_theta=True,retain_graph_flag = True)
p1, = plt.plot(T, sgd_losses, label='SGD')
p2, = plt.plot(T, rms_losses, label='RMS')
p3, = plt.plot(T, adam_losses, label='Adam')
p4, = plt.plot(x, lstm_losses, label='LSTM')
p1.set_dashes([2, 2, 2, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p2.set_dashes([4, 2, 8, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p3.set_dashes([3, 2, 10, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
#plt.yscale('log')
plt.legend(handles=[p1, p2, p3, p4])
plt.title('Losses')
plt.show()
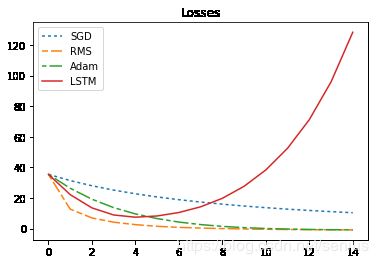
print("sum_loss:sgd={},rms={},adam={},lstm={}".format(sgd_sum_loss,rms_sum_loss,adam_sum_loss,lstm_sum_loss ))
sum_loss:sgd=289.9213562011719,rms=60.56287384033203,adam=117.2123031616211,lstm=554.2158203125
咦,为什么LSTM优化器那么差,根本没有优化效果?
先别着急质疑!因为我们还没有学习LSTM优化器!
用到的LSTM模型完全是随机初始化的!并且LSTM的参数在TRAIN_STEPS=[0,T]中的每个节点都是保持不变的!
下面我们就来优化LSTM优化器的参数!
不论是原始优化问题,还是隶属元学习的LSTM优化目标,我们都一个共同的学习目标:
θ ∗ = arg min θ ∈ Θ f ( θ ) \theta ^{*}= \arg\min_{\theta\in \Theta }f\left ( \theta \right ) θ∗=argθ∈Θminf(θ)
或者说我们希望迭代后的loss值变得很小,传统方法,是基于每个迭代周期,一步一步,让loss值变小,可以说,传统优化器进行梯度下降时所站的视角是在某个周期下的,那么,我们其实可以换一个视角,更全局的视角,即,我们希望所有周期迭代的loss值都很小,这和传统优化是不违背的,并且是全局的,这里做个比喻,优化就像是下棋,优化器就是
“下棋手 ”
如果一个棋手,在每走一步之前,都能看未来很多步被这一步的影响,那么它就能在当前步做出最佳策略,而LSTM的优化过程,就是把一个历史全局的“步”放在一起进行优化,所以LSTM的优化就具备了“瞻前顾后”的能力!
关于这一点,论文给出了一个期望loss的定义:
L ( ϕ ) = E f [ f ( θ ∗ ( f , ϕ ) ) ] L\left(\phi \right) =E_f \left[ f \left ( \theta ^{*}\left ( f,\phi \right )\right ) \right] L(ϕ)=Ef[f(θ∗(f,ϕ))]
但这个实现起来并不现实,我们只需要将其思想具体化。
-
Meta-optimizer优化:目标函数“所有周期的loss都要很小!”,而且这个目标函数是独立同分布采样的(比如,这里意味着任意初始化一个优化问题模型的参数,我们都希望这个优化器能够找到一个优化问题的稳定的解)
-
传统优化器:"对于当前的目标函数,只要这一步的loss比上一步的loss值要小就行”
特点 : 2.考虑优化器优化过程的历史全局性信息 3.独立同分布地采样优化问题目标函数的参数
接下来我们就站在更全局的角度,来优化LSTM优化器的参数
LSTM是循环神经网络,它可以连续记录并传递所有周期时刻的信息,其每个周期循环里的子图共同构建一个巨大的图,然后使用Back-Propagation Through Time (BPTT)来求导更新
lstm_losses,global_graph_loss= learn(LSTM_Optimizee,TRAINING_STEPS,retain_graph_flag =True) # [loss1,loss2,...lossT] 所有周期的loss
# 因为这里要保留所有周期的计算图所以retain_graph_flag =True
all_computing_graph_loss = torch.tensor(lstm_losses).sum()
#构建一个所有周期子图构成的总计算图,使用BPTT来梯度更新LSTM参数
print(all_computing_graph_loss,global_graph_loss )
print(global_graph_loss)
tensor(554.2158) tensor(554.2158, grad_fn=)
tensor(554.2158, grad_fn=)
可以看到,变量global_graph_loss保留了所有周期产生的计算图grad_fn=
下面针对LSTM的参数进行全局优化,优化目标:“所有周期之和的loss都很小”。
值得说明一下:在LSTM优化时的参数,是在所有Unroll_TRAIN_STEPS=[0,T]中保持不变的,在进行完所有Unroll_TRAIN_STEPS以后,再整体优化LSTM的参数。
这也就是论文里面提到的coordinate-wise,即“对每个时刻点都保持‘全局聪明’”,即学习到LSTM的参数是全局最优的了。因为我们是站在所有TRAIN_STEPS=[0,T]的视角下进行的优化!
优化LSTM优化器选择的是Adam优化器进行梯度下降
通过梯度下降法来优化 优化器
Global_Train_Steps = 2
def global_training(optimizee):
global_loss_list = []
adam_global_optimizer = torch.optim.Adam(optimizee.parameters(),lr = 0.0001)
_,global_loss_1 = learn(LSTM_Optimizee,TRAINING_STEPS,retain_graph_flag =True ,reset_theta = True)
#print(global_loss_1)
for i in range(Global_Train_Steps):
_,global_loss = learn(LSTM_Optimizee,TRAINING_STEPS,retain_graph_flag =True ,reset_theta = False)
#adam_global_optimizer.zero_grad()
print('xxx',[(z.grad,z.requires_grad) for z in optimizee.parameters() ])
#print(i,global_loss)
global_loss.backward() #每次都是优化这个固定的图,不可以释放动态图的缓存
#print('xxx',[(z.grad,z.requires_grad) for z in optimizee.parameters() ])
adam_global_optimizer.step()
print('xxx',[(z.grad,z.requires_grad) for z in optimizee.parameters() ])
global_loss_list.append(global_loss.detach_())
#print(global_loss)
return global_loss_list
# 要把图放进函数体内,直接赋值的话图会丢失
# 优化optimizee
global_loss_list = global_training(lstm)
xxx [(None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True)]
xxx [(None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True)]
xxx [(None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True)]
xxx [(None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True), (None, True)]
为什么loss值没有改变?为什么LSTM参数的梯度不存在的?
通过分析推理,我发现了LSTM参数的梯度为None,那么反向传播就完全没有更新LSTM的参数!
为什么参数的梯度为None呢,优化器并没有更新指定的LSTM的模型参数,一定是什么地方出了问题,我想了好久,还是做一些简单的实验来找一找问题吧。
ps: 其实写代码做实验的过程,也体现了人类本身学会学习的高级能力,那就是:通过实验来实现想法时,实验结果往往和预期差别很大,那一定有什么地方出了问题,盲目地大量试错法可能找不到真正问题所在,如何找到问题所在并解决,就是一种学会如何学习的能力,也是一种强化学习的能力。这里我采用的人类智能是:以小见大法。
In a word , if we want the machine achieving to AGI, it must imiate human’s ability of reasoning and finding where the problem is and figuring out how to solve the problem. Meta Learning contains this idea.
import torch
z= torch.empty(2)
torch.nn.init.uniform_(z , -2, 2)
z.requires_grad = True
z.retain_grad()
def f(z):
return (z*z).sum()
optimizer = torch.optim.Adam([z],lr=0.01)
grad =[]
losses= []
zgrad =[]
for i in range(2):
optimizer.zero_grad()
q = f(z)
loss = q**2
#z.retain_grad()
loss.backward(retain_graph = True)
optimizer.step()
#print(x,x.grad,loss,)
loss.retain_grad()
print(q.grad,q.requires_grad)
grad.append((z.grad))
losses.append(loss)
zgrad.append(q.grad)
print(grad)
print(losses)
print(zgrad)
None True
None True
[tensor([-44.4396, -36.7740]), tensor([-44.4396, -36.7740])]
[tensor(35.9191, grad_fn=), tensor(35.0999, grad_fn=)]
[None, None]
问题出在哪里?
经过多方面的实验修改,我发现LSTM的参数在每个周期内BPTT的周期内,并没有产生梯度!!怎么回事呢?我做了上面的小实验。
可以看到z.grad = None,但是z.requres_grad = True,z变量作为x变量的子节点,其在计算图中的梯度没有被保留或者没办法获取,那么我就应该通过修改一些PyTorch的代码,使得计算图中的叶子节点的梯度得以存在。然后我找到了retain_grad()这个函数,实验证明,它必须在backward()之前使用才能保存中间叶子节点的梯度!这样的方法也就适合于LSTM优化器模型参数的更新了吧?
那么如何保留LSTM的参数在每个周期中产生的梯度是接下来要修改的!
这是因为我计算loss = f(x),然后loss.backward() 这里的loss计算并没有和LSTM产生关系,我先来想一想loss和LSTM的关系在哪里?
论文里有一张图,可以作为参考:
LSTM参数的梯度来自于每次输出的“update”的梯度 update的梯度包含在生成的下一次迭代的参数x的梯度中
哦!因为参数 x t = x t − 1 + u p d a t e t − 1 x_t = x_{t-1}+update_{t-1} xt=xt−1+updatet−1 在BPTT的每个周期里 ∂ l o s s t ∂ θ L S T M = ∂ l o s s t ∂ u p d a t e t − 1 ∗ ∂ u p d a t e t − 1 ∂ θ L S T M \frac{\partial loss_t}{\partial \theta_{LSTM}}=\frac{\partial loss_t}{\partial update_{t-1}}*\frac{\partial update_{t-1}}{\partial \theta_{LSTM}} ∂θLSTM∂losst=∂updatet−1∂losst∗∂θLSTM∂updatet−1,那么我们想通过 l o s s 0 , l o s s 1 , . . , l o s s t loss_0,loss_1,..,loss_t loss0,loss1,..,losst之和来更新 θ L S T M \theta_{LSTM} θLSTM的话,就必须让梯度经过 x t x_t xt 中 的 u p d a t e t − 1 update_{t-1} updatet−1流回去,那么每次得到的 x t x_t xt就必须包含了上一次更新产生的图(可以想像,这个计算图是越来越大的),想一想我写的代码,似乎没有保留上一次的计算图在 x t x_t xt节点中,因为我用了x = x.detach_() 把x从图中拿了下来!这似乎是问题最关键所在!!!(而tensorflow静态图的构建,直接建立了一个完整所有周期的图,似乎Pytorch的动态图不合适?no,no)
(注:以上来自代码中的 x t x_t xt对应上图的 θ t \theta_t θt, u p d a t e t update_{t} updatet对应上图的 g t g_t gt)
我为什么会加入x = x.detach_() 是因为不加的话,x变成了子节点,下一次求导pytorch不允许,其实只需要加一行x.retain_grad()代码就行了,并且总的计算图的globa_graph_loss在逐步降低!问题解决!
目前在运行global_training(lstm)函数的话,就会发现LSTM的参数已经根据计算图中的梯度回流产生了梯度,每一步可以更新参数了,
但是这个BPTT算法用cpu算起来,有点慢了~
def learn(optimizee,unroll_train_steps,retain_graph_flag=False,reset_theta = False):
"""retain_graph_flag=False 默认每次loss_backward后 释放动态图
# reset_theta = False 默认每次学习前 不随机初始化参数"""
if reset_theta == True:
theta_new = torch.empty(DIM)
torch.nn.init.uniform_(theta_new,a=-1,b=1.0)
theta_init_new = torch.tensor(theta,dtype=torch.float32,requires_grad=True)
x = theta_init_new
else:
x = theta_init
global_loss_graph = 0 #这个是为LSTM优化器求所有loss相加产生计算图准备的
state = None
x.requires_grad = True
if optimizee.__name__ !='Adam':
losses = []
for i in range(unroll_train_steps):
loss = f(x)
#global_loss_graph += torch.exp(torch.Tensor([-i/20]))*loss
#global_loss_graph += (0.8*torch.log10(torch.Tensor([i+1]))+1)*loss
global_loss_graph += loss
loss.backward(retain_graph=retain_graph_flag) # 默认为False,当优化LSTM设置为True
update, state = optimizee(x.grad, state)
losses.append(loss)
x = x + update
# x = x.detach_()
#这个操作 直接把x中包含的图给释放了,
#那传递给下次训练的x从子节点变成了叶节点,那么梯度就不能沿着这个路回传了,
#之前写这一步是因为这个子节点在下一次迭代不可以求导,那么应该用x.retain_grad()这个操作,
#然后不需要每次新的的开始给x.requires_grad = True
x.retain_grad()
#print(x.retain_grad())
#print(x)
return losses ,global_loss_graph
else:
losses = []
x.requires_grad = True
optimizee= torch.optim.Adam( [x],lr=0.1 )
for i in range(unroll_train_steps):
optimizee.zero_grad()
loss = f(x)
global_loss_graph += loss
loss.backward(retain_graph=retain_graph_flag)
optimizee.step()
losses.append(loss.detach_())
#print(x)
return losses,global_loss_graph
Global_Train_Steps = 1000
def global_training(optimizee):
global_loss_list = []
adam_global_optimizer = torch.optim.Adam([{'params':optimizee.parameters()},{'params':Linear.parameters()}],lr = 0.0001)
_,global_loss_1 = learn(LSTM_Optimizee,TRAINING_STEPS,retain_graph_flag =True ,reset_theta = True)
print(global_loss_1)
for i in range(Global_Train_Steps):
_,global_loss = learn(LSTM_Optimizee,TRAINING_STEPS,retain_graph_flag =True ,reset_theta = False)
adam_global_optimizer.zero_grad()
#print(i,global_loss)
global_loss.backward() #每次都是优化这个固定的图,不可以释放动态图的缓存
#print('xxx',[(z,z.requires_grad) for z in optimizee.parameters() ])
adam_global_optimizer.step()
#print('xxx',[(z.grad,z.requires_grad) for z in optimizee.parameters() ])
global_loss_list.append(global_loss.detach_())
print(global_loss)
return global_loss_list
# 要把图放进函数体内,直接赋值的话图会丢失
# 优化optimizee
global_loss_list = global_training(lstm)
tensor(193.6147, grad_fn=)
tensor(7.6411)
计算图不再丢失了,LSTM的参数的梯度经过计算图的流动已经产生了!
Global_T = np.arange(Global_Train_Steps)
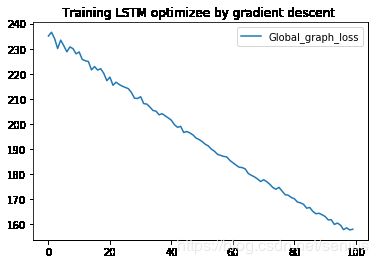
p1, = plt.plot(Global_T, global_loss_list, label='Global_graph_loss')
plt.legend(handles=[p1])
plt.title('Training LSTM optimizee by gradient descent ')
plt.show()
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
STEPS = 15
x = np.arange(STEPS)
for _ in range(2):
sgd_losses, sgd_sum_loss = learn(SGD,STEPS,reset_theta=True)
rms_losses, rms_sum_loss = learn(RMS,STEPS,reset_theta=True)
adam_losses, adam_sum_loss = learn(Adam,STEPS,reset_theta=True)
lstm_losses,lstm_sum_loss = learn(LSTM_Optimizee,STEPS,reset_theta=True,retain_graph_flag = True)
p1, = plt.plot(x, sgd_losses, label='SGD')
p2, = plt.plot(x, rms_losses, label='RMS')
p3, = plt.plot(x, adam_losses, label='Adam')
p4, = plt.plot(x, lstm_losses, label='LSTM')
p1.set_dashes([2, 2, 2, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p2.set_dashes([4, 2, 8, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p3.set_dashes([3, 2, 10, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
plt.legend(handles=[p1, p2, p3, p4])
#plt.yscale('log')
plt.title('Losses')
plt.show()
print("sum_loss:sgd={},rms={},adam={},lstm={}".format(sgd_sum_loss,rms_sum_loss,adam_sum_loss,lstm_sum_loss ))
sum_loss:sgd=48.513607025146484,rms=5.537945747375488,adam=11.781242370605469,lstm=15.151629447937012
sum_loss:sgd=48.513607025146484,rms=5.537945747375488,adam=11.781242370605469,lstm=15.151629447937012
可以看出来,经过优化后的LSTM优化器,似乎已经开始掌握如何优化的方法,即我们基本训练出了一个可以训练模型的优化器!
但是效果并不是很明显!
不过代码编写取得一定进展\ (0 …0) /,接下就是让效果更明显,性能更稳定了吧?
不过我先再多测试一些周期看看LSTM的优化效果!先别高兴太早!
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
STEPS = 50
x = np.arange(STEPS)
for _ in range(1):
sgd_losses, sgd_sum_loss = learn(SGD,STEPS,reset_theta=True)
rms_losses, rms_sum_loss = learn(RMS,STEPS,reset_theta=True)
adam_losses, adam_sum_loss = learn(Adam,STEPS,reset_theta=True)
lstm_losses,lstm_sum_loss = learn(LSTM_Optimizee,STEPS,reset_theta=True,retain_graph_flag = True)
p1, = plt.plot(x, sgd_losses, label='SGD')
p2, = plt.plot(x, rms_losses, label='RMS')
p3, = plt.plot(x, adam_losses, label='Adam')
p4, = plt.plot(x, lstm_losses, label='LSTM')
plt.legend(handles=[p1, p2, p3, p4])
#plt.yscale('log')
plt.title('Losses')
plt.show()
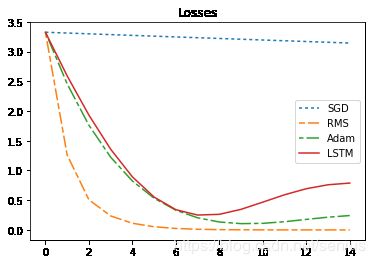
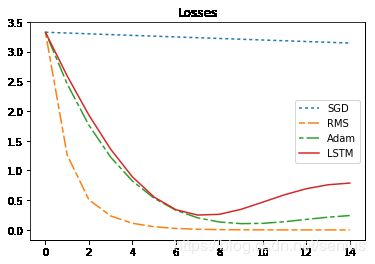
print("sum_loss:sgd={},rms={},adam={},lstm={}".format(sgd_sum_loss,rms_sum_loss,adam_sum_loss,lstm_sum_loss ))
sum_loss:sgd=150.99790954589844,rms=5.940474033355713,adam=14.17563247680664,lstm=268.0199279785156
又出了什么幺蛾子?
即我们基本训练出了一个可以训练模型的优化器!但是 经过更长周期的测试,发现训练好的优化器只是优化了指定的周期的loss,而并没有学会“全局优化”的本领,这个似乎是个大问题!
不同周期下输入LSTM的梯度幅值数量级是不在一个等级上面,要处理一下!
论文里面提到了对梯度的预处理,即处理不同数量级别的梯度,来进行BPTT,因为每个周期的产生的梯度幅度是完全不在一个数量级,前期梯度下降很快,中后期梯度下降平缓,这个对于LSTM的输入,变化裕度太大,应该归一化,但这个我并没有考虑,接下似乎该写这个部分的代码了
论文里提到了:
One potential challenge in training optimizers is that different input coordinates (i.e. the gradients w.r.t. different
optimizee parameters) can have very different magnitudes.
This is indeed the case e.g. when the optimizee is a neural network and different parameters
correspond to weights in different layers.
This can make training an optimizer difficult, because neural networks
naturally disregard small variations in input signals and concentrate on bigger input values.
怎么处理:用梯度的(归一化幅值,方向)二元组替代原梯度作为LSTM的输入
To this aim we propose to preprocess the optimizer’s inputs.
One solution would be to give the optimizer ( log ( ∣ ∇ ∣ ) , sgn ( ∇ ) ) \left(\log(|\nabla|),\,\operatorname{sgn}(\nabla)\right) (log(∣∇∣),sgn(∇)) as an input, where
∇ \nabla ∇ is the gradient in the current timestep.
This has a problem that log ( ∣ ∇ ∣ ) \log(|\nabla|) log(∣∇∣) diverges for ∇ → 0 \nabla \rightarrow 0 ∇→0.
Therefore, we use the following preprocessing formula
∇ \nabla ∇ is the gradient in the current timestep.
This has a problem that log ( ∣ ∇ ∣ ) \log(|\nabla|) log(∣∇∣) diverges for ∇ → 0 \nabla \rightarrow 0 ∇→0.
Therefore, we use the following preprocessing formula
∇ k → { ( log ( ∣ ∇ ∣ ) p , sgn ( ∇ ) ) if ∣ ∇ ∣ ≥ e − p ( − 1 , e p ∇ ) otherwise \nabla^k\rightarrow \left\{\begin{matrix} \left(\frac{\log(|\nabla|)}{p}\,, \operatorname{sgn}(\nabla)\right)& \text{if } |\nabla| \geq e^{-p}\\ (-1, e^p \nabla) & \text{otherwise} \end{matrix}\right. ∇k→{(plog(∣∇∣),sgn(∇))(−1,ep∇)if ∣∇∣≥e−potherwise
作者将不同幅度和方向下的梯度,用一个标准化到 [ − 1 , 1 ] [-1,1] [−1,1]的幅值和符号方向二元组来表示原来的梯度张量!这样将有助于LSTM的参数学习!
那我就重新定义LSTM优化器!
Layers = 2
Hidden_nums = 20
Input_DIM = DIM
Output_DIM = DIM
# "coordinate-wise" RNN
#lstm1=torch.nn.LSTM(Input_DIM*2,Hidden_nums ,Layers)
#Linear = torch.nn.Linear(Hidden_nums,Output_DIM)
class LSTM_Optimizee_Model(torch.nn.Module):
"""LSTM优化器"""
def __init__(self,input_size,output_size, hidden_size, num_stacks, batchsize, preprocess = True ,p = 10 ,output_scale = 1):
super(LSTM_Optimizee_Model,self).__init__()
self.preprocess_flag = preprocess
self.p = p
self.output_scale = output_scale #论文
self.lstm = torch.nn.LSTM(input_size, hidden_size, num_stacks)
self.Linear = torch.nn.Linear(hidden_size,output_size)
#elf.lstm = torch.nn.LSTM(10, 20,2)
#elf.Linear = torch.nn.Linear(20,10)
def LogAndSign_Preprocess_Gradient(self,gradients):
"""
Args:
gradients: `Tensor` of gradients with shape `[d_1, ..., d_n]`.
p : `p` > 0 is a parameter controlling how small gradients are disregarded
Returns:
`Tensor` with shape `[d_1, ..., d_n-1, 2 * d_n]`. The first `d_n` elements
along the nth dimension correspond to the `log output` \in [-1,1] and the remaining
`d_n` elements to the `sign output`.
"""
p = self.p
log = torch.log(torch.abs(gradients))
clamp_log = torch.clamp(log/p , min = -1.0,max = 1.0)
clamp_sign = torch.clamp(torch.exp(torch.Tensor(p))*gradients, min = -1.0, max =1.0)
return torch.cat((clamp_log,clamp_sign),dim = -1) #在gradients的最后一维input_dims拼接
def Output_Gradient_Increment_And_Update_LSTM_Hidden_State(self, input_gradients, prev_state):
"""LSTM的核心操作"""
if prev_state is None: #init_state
prev_state = (torch.zeros(Layers,batchsize,Hidden_nums),
torch.zeros(Layers,batchsize,Hidden_nums))
update , next_state = self.lstm(input_gradients, prev_state)
update = Linear(update) * self.output_scale #因为LSTM的输出是当前步的Hidden,需要变换到output的相同形状上
return update, next_state
def forward(self,gradients, prev_state):
#LSTM的输入为梯度,pytorch要求torch.nn.lstm的输入为(1,batchsize,input_dim)
#原gradient.size()=torch.size[5] ->[1,1,5]
gradients = gradients.unsqueeze(0).unsqueeze(0)
if self.preprocess_flag == True:
gradients = self.LogAndSign_Preprocess_Gradient(gradients)
update , next_state = self.Output_Gradient_Increment_And_Update_LSTM_Hidden_State(gradients , prev_state)
# Squeeze to make it a single batch again.[1,1,5]->[5]
update = update.squeeze().squeeze()
return update , next_state
LSTM_Optimizee = LSTM_Optimizee_Model(Input_DIM*2, Output_DIM, Hidden_nums ,Layers , batchsize=1,)
grads = torch.randn(10)*10
print(grads.size())
update,state = LSTM_Optimizee(grads,None)
print(update.size(),)
torch.Size([10])
torch.Size([10])
编写成功!
执行!
def learn(optimizee,unroll_train_steps,retain_graph_flag=False,reset_theta = False):
"""retain_graph_flag=False 默认每次loss_backward后 释放动态图
# reset_theta = False 默认每次学习前 不随机初始化参数"""
if reset_theta == True:
theta_new = torch.empty(DIM)
torch.nn.init.uniform_(theta_new,a=-1,b=1.0)
theta_init_new = torch.tensor(theta,dtype=torch.float32,requires_grad=True)
x = theta_init_new
else:
x = theta_init
global_loss_graph = 0 #这个是为LSTM优化器求所有loss相加产生计算图准备的
state = None
x.requires_grad = True
if optimizee!='Adam':
losses = []
for i in range(unroll_train_steps):
loss = f(x)
#global_loss_graph += torch.exp(torch.Tensor([-i/20]))*loss
#global_loss_graph += (0.8*torch.log10(torch.Tensor([i+1]))+1)*loss
global_loss_graph += loss
# print('loss{}:'.format(i),loss)
loss.backward(retain_graph=retain_graph_flag) # 默认为False,当优化LSTM设置为True
update, state = optimizee(x.grad, state)
#print(update)
losses.append(loss)
x = x + update
x.retain_grad()
return losses ,global_loss_graph
else:
losses = []
x.requires_grad = True
optimizee= torch.optim.Adam( [x],lr=0.1 )
for i in range(unroll_train_steps):
optimizee.zero_grad()
loss = f(x)
global_loss_graph += loss
loss.backward(retain_graph=retain_graph_flag)
optimizee.step()
losses.append(loss.detach_())
#print(x)
return losses,global_loss_graph
Global_Train_Steps = 100
def global_training(optimizee):
global_loss_list = []
adam_global_optimizer = torch.optim.Adam(optimizee.parameters(),lr = 0.0001)
_,global_loss_1 = learn(optimizee,TRAINING_STEPS,retain_graph_flag =True ,reset_theta = True)
print(global_loss_1)
for i in range(Global_Train_Steps):
_,global_loss = learn(optimizee,TRAINING_STEPS,retain_graph_flag =True ,reset_theta = False)
adam_global_optimizer.zero_grad()
#print(i,global_loss)
global_loss.backward() #每次都是优化这个固定的图,不可以释放动态图的缓存
#print('xxx',[(z,z.requires_grad) for z in optimizee.parameters() ])
adam_global_optimizer.step()
#print('xxx',[(z.grad,z.requires_grad) for z in optimizee.parameters() ])
global_loss_list.append(global_loss.detach_())
print(global_loss)
return global_loss_list
# 要把图放进函数体内,直接赋值的话图会丢失
# 优化optimizee
global_loss_list = global_training(LSTM_Optimizee)
tensor(239.6029, grad_fn=)
tensor(158.0625)
Global_T = np.arange(Global_Train_Steps)
p1, = plt.plot(Global_T, global_loss_list, label='Global_graph_loss')
plt.legend(handles=[p1])
plt.title('Training LSTM optimizee by gradient descent ')
plt.show()
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
STEPS = 30
x = np.arange(STEPS)
Adam = 'Adam'
for _ in range(1):
sgd_losses, sgd_sum_loss = learn(SGD,STEPS,reset_theta=True)
rms_losses, rms_sum_loss = learn(RMS,STEPS,reset_theta=True)
adam_losses, adam_sum_loss = learn(Adam,STEPS,reset_theta=True)
lstm_losses,lstm_sum_loss = learn(LSTM_Optimizee,STEPS,reset_theta=True,retain_graph_flag = True)
p1, = plt.plot(x, sgd_losses, label='SGD')
p2, = plt.plot(x, rms_losses, label='RMS')
p3, = plt.plot(x, adam_losses, label='Adam')
p4, = plt.plot(x, lstm_losses, label='LSTM')
p1.set_dashes([2, 2, 2, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p2.set_dashes([4, 2, 8, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p3.set_dashes([3, 2, 10, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
plt.legend(handles=[p1, p2, p3, p4])
plt.title('Losses')
plt.show()
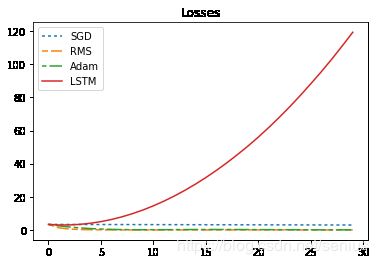
print("sum_loss:sgd={},rms={},adam={},lstm={}".format(sgd_sum_loss,rms_sum_loss,adam_sum_loss,lstm_sum_loss ))
sum_loss:sgd=94.19924926757812,rms=5.705832481384277,adam=13.772469520568848,lstm=1224.2393798828125
为什么loss出现了NaN???为什么优化器的泛化性能很差??很烦
即超过Unroll周期以后,LSTM优化器不再具备优化性能???
然后我又回顾论文,发现,对优化器进行优化的每个周期开始,要重新随机化,优化问题的参数,即确保我们的LSTM不针对一个特定优化问题过拟合,什么?优化器也会过拟合!是的!l
论文里面其实也有提到:
Given a distribution of functions f f f we will write
the expected loss as:
L ( ϕ ) = E f [ f ( θ ∗ ( f , ϕ ) ) ] ( 1 ) L\left(\phi \right) =E_f \left[ f \left ( \theta ^{*}\left ( f,\phi \right )\right ) \right](1) L(ϕ)=Ef[f(θ∗(f,ϕ))](1)
其中f是随机分布的,那么就需要在Unroll的初始进行从IID 标准Gaussian分布随机采样函数的参数
另外我完善了代码,根据原作代码实现,把LSTM的输出乘以一个系数0.01,那么LSTM的学习变得更加快速了。
还有一个地方,就是作者优化optimiee用了100个周期,即5个连续的Unroll周期,这一点似乎我之前也没有考虑到!
以上是代码编写遇到的种种问题,下面就是最完整的有效代码了!!!
我们考虑优化论文中提到的Quadratic函数,并且用论文中完全一样的实验条件!
f ( θ ) = ∥ W θ − y ∥ 2 2 f(\theta) = \|W\theta - y\|_2^2 f(θ)=∥Wθ−y∥22
for different 10x10 matrices W W W and 10-dimensional vectors y y y whose elements are drawn
from an IID Gaussian distribution.
Optimizers were trained by optimizing random functions from this family and
tested on newly sampled functions from the same distribution. Each function was
optimized for 100 steps and the trained optimizers were unrolled for 20 steps.
We have not used any preprocessing, nor postprocessing.
# coding: utf-8
# Learning to learn by gradient descent by gradient descent
# =========================#
# https://arxiv.org/abs/1611.03824
# https://yangsenius.github.io/blog/LSTM_Meta/
# https://github.com/yangsenius/learning-to-learn-by-pytorch
# author:yangsen
# #### “通过梯度下降来学习如何通过梯度下降学习”
# #### 要让优化器学会这样 "为了更好地得到,要先去舍弃" 这样类似的知识!
import torch
import torch.nn as nn
from timeit import default_timer as timer
##################### 优化问题 ##########################
USE_CUDA = False
DIM = 10
batchsize = 128
if torch.cuda.is_available():
USE_CUDA = True
USE_CUDA = False
print('\n\nUSE_CUDA = {}\n\n'.format(USE_CUDA))
def f(W,Y,x):
"""quadratic function : f(\theta) = \|W\theta - y\|_2^2"""
if USE_CUDA:
W = W.cuda()
Y = Y.cuda()
x = x.cuda()
return ((torch.matmul(W,x.unsqueeze(-1)).squeeze()-Y)**2).sum(dim=1).mean(dim=0)
###############################################################
###################### 手工的优化器 ###################
def SGD(gradients, state, learning_rate=0.001):
return -gradients*learning_rate, state
def RMS(gradients, state, learning_rate=0.01, decay_rate=0.9):
if state is None:
state = torch.zeros(DIM)
if USE_CUDA == True:
state = state.cuda()
state = decay_rate*state + (1-decay_rate)*torch.pow(gradients, 2)
update = -learning_rate*gradients / (torch.sqrt(state+1e-5))
return update, state
def adam():
return torch.optim.Adam()
##########################################################
##################### 自动 LSTM 优化器模型 ##########################
class LSTM_Optimizee_Model(torch.nn.Module):
"""LSTM优化器"""
def __init__(self,input_size,output_size, hidden_size, num_stacks, batchsize, preprocess = True ,p = 10 ,output_scale = 1):
super(LSTM_Optimizee_Model,self).__init__()
self.preprocess_flag = preprocess
self.p = p
self.input_flag = 2
if preprocess != True:
self.input_flag = 1
self.output_scale = output_scale #论文
self.lstm = torch.nn.LSTM(input_size*self.input_flag, hidden_size, num_stacks)
self.Linear = torch.nn.Linear(hidden_size,output_size) #1-> output_size
def LogAndSign_Preprocess_Gradient(self,gradients):
"""
Args:
gradients: `Tensor` of gradients with shape `[d_1, ..., d_n]`.
p : `p` > 0 is a parameter controlling how small gradients are disregarded
Returns:
`Tensor` with shape `[d_1, ..., d_n-1, 2 * d_n]`. The first `d_n` elements
along the nth dimension correspond to the `log output` \in [-1,1] and the remaining
`d_n` elements to the `sign output`.
"""
p = self.p
log = torch.log(torch.abs(gradients))
clamp_log = torch.clamp(log/p , min = -1.0,max = 1.0)
clamp_sign = torch.clamp(torch.exp(torch.Tensor(p))*gradients, min = -1.0, max =1.0)
return torch.cat((clamp_log,clamp_sign),dim = -1) #在gradients的最后一维input_dims拼接
def Output_Gradient_Increment_And_Update_LSTM_Hidden_State(self, input_gradients, prev_state):
"""LSTM的核心操作
coordinate-wise LSTM """
if prev_state is None: #init_state
prev_state = (torch.zeros(Layers,batchsize,Hidden_nums),
torch.zeros(Layers,batchsize,Hidden_nums))
if USE_CUDA :
prev_state = (torch.zeros(Layers,batchsize,Hidden_nums).cuda(),
torch.zeros(Layers,batchsize,Hidden_nums).cuda())
update , next_state = self.lstm(input_gradients, prev_state)
update = self.Linear(update) * self.output_scale #因为LSTM的输出是当前步的Hidden,需要变换到output的相同形状上
return update, next_state
def forward(self,input_gradients, prev_state):
if USE_CUDA:
input_gradients = input_gradients.cuda()
#LSTM的输入为梯度,pytorch要求torch.nn.lstm的输入为(1,batchsize,input_dim)
#原gradient.size()=torch.size[5] ->[1,1,5]
gradients = input_gradients.unsqueeze(0)
if self.preprocess_flag == True:
gradients = self.LogAndSign_Preprocess_Gradient(gradients)
update , next_state = self.Output_Gradient_Increment_And_Update_LSTM_Hidden_State(gradients , prev_state)
# Squeeze to make it a single batch again.[1,1,5]->[5]
update = update.squeeze().squeeze()
return update , next_state
################# 优化器模型参数 ##############################
Layers = 2
Hidden_nums = 20
Input_DIM = DIM
Output_DIM = DIM
output_scale_value=1
####### 构造一个优化器 #######
LSTM_Optimizee = LSTM_Optimizee_Model(Input_DIM, Output_DIM, Hidden_nums ,Layers , batchsize=batchsize,\
preprocess=False,output_scale=output_scale_value)
print(LSTM_Optimizee)
if USE_CUDA:
LSTM_Optimizee = LSTM_Optimizee.cuda()
###################### 优化问题目标函数的学习过程 ###############
class Learner( object ):
"""
Args :
`f` : 要学习的问题
`optimizee` : 使用的优化器
`train_steps` : 对于其他SGD,Adam等是训练周期,对于LSTM训练时的展开周期
`retain_graph_flag=False` : 默认每次loss_backward后 释放动态图
`reset_theta = False ` : 默认每次学习前 不随机初始化参数
`reset_function_from_IID_distirbution = True` : 默认从分布中随机采样函数
Return :
`losses` : reserves each loss value in each iteration
`global_loss_graph` : constructs the graph of all Unroll steps for LSTM's BPTT
"""
def __init__(self, f , optimizee, train_steps ,
eval_flag = False,
retain_graph_flag=False,
reset_theta = False ,
reset_function_from_IID_distirbution = True):
self.f = f
self.optimizee = optimizee
self.train_steps = train_steps
#self.num_roll=num_roll
self.eval_flag = eval_flag
self.retain_graph_flag = retain_graph_flag
self.reset_theta = reset_theta
self.reset_function_from_IID_distirbution = reset_function_from_IID_distirbution
self.init_theta_of_f()
self.state = None
self.global_loss_graph = 0 #这个是为LSTM优化器求所有loss相加产生计算图准备的
self.losses = [] # 保存每个训练周期的loss值
def init_theta_of_f(self,):
''' 初始化 优化问题 f 的参数 '''
self.DIM = 10
self.batchsize = 128
self.W = torch.randn(batchsize,DIM,DIM) #代表 已知的数据 # 独立同分布的标准正太分布
self.Y = torch.randn(batchsize,DIM)
self.x = torch.zeros(self.batchsize,self.DIM)
self.x.requires_grad = True
if USE_CUDA:
self.W = self.W.cuda()
self.Y = self.Y.cuda()
self.x = self.x.cuda()
def Reset_Or_Reuse(self , x , W , Y , state, num_roll):
''' re-initialize the `W, Y, x , state` at the begining of each global training
IF `num_roll` == 0 '''
reset_theta =self.reset_theta
reset_function_from_IID_distirbution = self.reset_function_from_IID_distirbution
if num_roll == 0 and reset_theta == True:
theta = torch.zeros(batchsize,DIM)
theta_init_new = torch.tensor(theta,dtype=torch.float32,requires_grad=True)
x = theta_init_new
################ 每次全局训练迭代,从独立同分布的Normal Gaussian采样函数 ##################
if num_roll == 0 and reset_function_from_IID_distirbution == True :
W = torch.randn(batchsize,DIM,DIM) #代表 已知的数据 # 独立同分布的标准正太分布
Y = torch.randn(batchsize,DIM) #代表 数据的标签 # 独立同分布的标准正太分布
if num_roll == 0:
state = None
print('reset W, x , Y, state ')
if USE_CUDA:
W = W.cuda()
Y = Y.cuda()
x = x.cuda()
x.retain_grad()
return x , W , Y , state
def __call__(self, num_roll=0) :
'''
Total Training steps = Unroll_Train_Steps * the times of `Learner` been called
SGD,RMS,LSTM 用上述定义的
Adam优化器直接使用pytorch里的,所以代码上有区分 后面可以完善!'''
f = self.f
x , W , Y , state = self.Reset_Or_Reuse(self.x , self.W , self.Y , self.state , num_roll )
self.global_loss_graph = 0 #每个unroll的开始需要 重新置零
optimizee = self.optimizee
print('state is None = {}'.format(state == None))
if optimizee!='Adam':
for i in range(self.train_steps):
loss = f(W,Y,x)
#self.global_loss_graph += (0.8*torch.log10(torch.Tensor([i+1]))+1)*loss
self.global_loss_graph += loss
loss.backward(retain_graph=self.retain_graph_flag) # 默认为False,当优化LSTM设置为True
update, state = optimizee(x.grad, state)
self.losses.append(loss)
x = x + update
x.retain_grad()
update.retain_grad()
if state is not None:
self.state = (state[0].detach(),state[1].detach())
return self.losses ,self.global_loss_graph
else: #Pytorch Adam
x.detach_()
x.requires_grad = True
optimizee= torch.optim.Adam( [x],lr=0.1 )
for i in range(self.train_steps):
optimizee.zero_grad()
loss = f(W,Y,x)
self.global_loss_graph += loss
loss.backward(retain_graph=self.retain_graph_flag)
optimizee.step()
self.losses.append(loss.detach_())
return self.losses, self.global_loss_graph
####### LSTM 优化器的训练过程 Learning to learn ###############
def Learning_to_learn_global_training(optimizee, global_taining_steps, Optimizee_Train_Steps, UnRoll_STEPS, Evaluate_period ,optimizer_lr=0.1):
""" Training the LSTM optimizee . Learning to learn
Args:
`optimizee` : DeepLSTMCoordinateWise optimizee model
`global_taining_steps` : how many steps for optimizer training o可以ptimizee
`Optimizee_Train_Steps` : how many step for optimizee opimitzing each function sampled from IID.
`UnRoll_STEPS` :: how many steps for LSTM optimizee being unrolled to construct a computing graph to BPTT.
"""
global_loss_list = []
Total_Num_Unroll = Optimizee_Train_Steps // UnRoll_STEPS
adam_global_optimizer = torch.optim.Adam(optimizee.parameters(),lr = optimizer_lr)
LSTM_Learner = Learner(f, optimizee, UnRoll_STEPS, retain_graph_flag=True, reset_theta=True,)
#这里考虑Batchsize代表IID的话,那么就可以不需要每次都重新IID采样
#即reset_function_from_IID_distirbution = False 否则为True
best_sum_loss = 999999
best_final_loss = 999999
best_flag = False
for i in range(Global_Train_Steps):
print('\n=======> global training steps: {}'.format(i))
for num in range(Total_Num_Unroll):
start = timer()
_,global_loss = LSTM_Learner(num)
adam_global_optimizer.zero_grad()
global_loss.backward()
adam_global_optimizer.step()
# print('xxx',[(z.grad,z.requires_grad) for z in optimizee.lstm.parameters() ])
global_loss_list.append(global_loss.detach_())
time = timer() - start
#if i % 10 == 0:
print('-> time consuming [{:.1f}s] optimizee train steps : [{}] | Global_Loss = [{:.1f}] '\
.format(time,(num +1)* UnRoll_STEPS,global_loss,))
if (i + 1) % Evaluate_period == 0:
best_sum_loss, best_final_loss, best_flag = evaluate(best_sum_loss,best_final_loss,best_flag , optimizer_lr)
return global_loss_list,best_flag
def evaluate(best_sum_loss,best_final_loss, best_flag,lr):
print('\n --> evalute the model')
STEPS = 100
LSTM_learner = Learner(f , LSTM_Optimizee, STEPS, eval_flag=True,reset_theta=True, retain_graph_flag=True)
lstm_losses, sum_loss = LSTM_learner()
try:
best = torch.load('best_loss.txt')
except IOError:
print ('can not find best_loss.txt')
pass
else:
best_sum_loss = best[0]
best_final_loss = best[1]
print("load_best_final_loss and sum_loss")
if lstm_losses[-1] < best_final_loss and sum_loss < best_sum_loss:
best_final_loss = lstm_losses[-1]
best_sum_loss = sum_loss
print('\n\n===> update new best of final LOSS[{}]: = {}, best_sum_loss ={}'.format(STEPS, best_final_loss,best_sum_loss))
torch.save(LSTM_Optimizee.state_dict(),'best_LSTM_optimizer.pth')
torch.save([best_sum_loss ,best_final_loss,lr ],'best_loss.txt')
best_flag = True
return best_sum_loss, best_final_loss, best_flag
USE_CUDA = False
LSTM_Optimizee_Model(
(lstm): LSTM(10, 20, num_layers=2)
(Linear): Linear(in_features=20, out_features=10, bias=True)
)
我们先来看看随机初始化的LSTM优化器的效果
############# 注意:接上一片段的代码!! #######################3#
########################## before learning LSTM optimizee ###############################
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
STEPS = 100
x = np.arange(STEPS)
Adam = 'Adam' #因为这里Adam使用Pytorch
for _ in range(1):
SGD_Learner = Learner(f , SGD, STEPS, eval_flag=True,reset_theta=True,)
RMS_Learner = Learner(f , RMS, STEPS, eval_flag=True,reset_theta=True,)
Adam_Learner = Learner(f , Adam, STEPS, eval_flag=True,reset_theta=True,)
LSTM_learner = Learner(f , LSTM_Optimizee, STEPS, eval_flag=True,reset_theta=True,retain_graph_flag=True)
sgd_losses, sgd_sum_loss = SGD_Learner()
rms_losses, rms_sum_loss = RMS_Learner()
adam_losses, adam_sum_loss = Adam_Learner()
lstm_losses, lstm_sum_loss = LSTM_learner()
p1, = plt.plot(x, sgd_losses, label='SGD')
p2, = plt.plot(x, rms_losses, label='RMS')
p3, = plt.plot(x, adam_losses, label='Adam')
p4, = plt.plot(x, lstm_losses, label='LSTM')
p1.set_dashes([2, 2, 2, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p2.set_dashes([4, 2, 8, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p3.set_dashes([3, 2, 10, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
plt.yscale('log')
plt.legend(handles=[p1, p2, p3, p4])
plt.title('Losses')
plt.show()
print("\n\nsum_loss:sgd={},rms={},adam={},lstm={}".format(sgd_sum_loss,rms_sum_loss,adam_sum_loss,lstm_sum_loss ))
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
sum_loss:sgd=945.0716552734375,rms=269.4500427246094,adam=134.2750244140625,lstm=562912.125
随机初始化的LSTM优化器没有任何效果,loss发散了!但问题不大
####### 注意:接上一段的代码!!
#################### Learning to learn (优化optimizee) ######################
Global_Train_Steps = 1000 #可修改
Optimizee_Train_Steps = 100
UnRoll_STEPS = 20
Evaluate_period = 1 #可修改
optimizer_lr = 0.1 #可修改
global_loss_list ,flag = Learning_to_learn_global_training( LSTM_Optimizee,
Global_Train_Steps,
Optimizee_Train_Steps,
UnRoll_STEPS,
Evaluate_period,
optimizer_lr)
######################################################################3#
########################## show learning process results
#torch.load('best_LSTM_optimizer.pth'))
#import numpy as np
#import matplotlib
#import matplotlib.pyplot as plt
#Global_T = np.arange(len(global_loss_list))
#p1, = plt.plot(Global_T, global_loss_list, label='Global_graph_loss')
#plt.legend(handles=[p1])
#plt.title('Training LSTM optimizee by gradient descent ')
#plt.show()
=======> global training steps: 0
reset W, x , Y, state
state is None = True
-> time consuming [0.2s] optimizee train steps : [20] | Global_Loss = [4009.4]
state is None = False
-> time consuming [0.3s] optimizee train steps : [40] | Global_Loss = [21136.7]
state is None = False
-> time consuming [0.2s] optimizee train steps : [60] | Global_Loss = [136640.5]
state is None = False
-> time consuming [0.2s] optimizee train steps : [80] | Global_Loss = [4017.9]
state is None = False
-> time consuming [0.2s] optimizee train steps : [100] | Global_Loss = [9107.1]
--> evalute the model
reset W, x , Y, state
state is None = True
...........
...........
输出结果已经省略大部分
接下来看一下优化好的LSTM优化器模型和SGD,RMSProp,Adam的优化性能对比表现吧~
鸡冻
############### **注意: **接上一片段的代码****
######################################################################3#
########################## show contrast results SGD,ADAM, RMS ,LSTM ###############################
import copy
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
if flag ==True :
print('\n==== > load best LSTM model')
last_state_dict = copy.deepcopy(LSTM_Optimizee.state_dict())
torch.save(LSTM_Optimizee.state_dict(),'final_LSTM_optimizer.pth')
LSTM_Optimizee.load_state_dict( torch.load('best_LSTM_optimizer.pth'))
LSTM_Optimizee.load_state_dict(torch.load('best_LSTM_optimizer.pth'))
#LSTM_Optimizee.load_state_dict(torch.load('final_LSTM_optimizer.pth'))
STEPS = 100
x = np.arange(STEPS)
Adam = 'Adam' #因为这里Adam使用Pytorch
for _ in range(2): #可以多试几次测试实验,LSTM不稳定
SGD_Learner = Learner(f , SGD, STEPS, eval_flag=True,reset_theta=True,)
RMS_Learner = Learner(f , RMS, STEPS, eval_flag=True,reset_theta=True,)
Adam_Learner = Learner(f , Adam, STEPS, eval_flag=True,reset_theta=True,)
LSTM_learner = Learner(f , LSTM_Optimizee, STEPS, eval_flag=True,reset_theta=True,retain_graph_flag=True)
sgd_losses, sgd_sum_loss = SGD_Learner()
rms_losses, rms_sum_loss = RMS_Learner()
adam_losses, adam_sum_loss = Adam_Learner()
lstm_losses, lstm_sum_loss = LSTM_learner()
p1, = plt.plot(x, sgd_losses, label='SGD')
p2, = plt.plot(x, rms_losses, label='RMS')
p3, = plt.plot(x, adam_losses, label='Adam')
p4, = plt.plot(x, lstm_losses, label='LSTM')
p1.set_dashes([2, 2, 2, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p2.set_dashes([4, 2, 8, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
p3.set_dashes([3, 2, 10, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
#p4.set_dashes([2, 2, 10, 2]) # 2pt line, 2pt break, 10pt line, 2pt break
plt.yscale('log')
plt.legend(handles=[p1, p2, p3, p4])
plt.title('Losses')
plt.show()
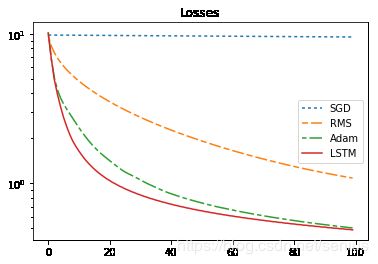
print("\n\nsum_loss:sgd={},rms={},adam={},lstm={}".format(sgd_sum_loss,rms_sum_loss,adam_sum_loss,lstm_sum_loss ))
==== > load best LSTM model
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
sum_loss:sgd=967.908935546875,rms=257.03814697265625,adam=122.87742614746094,lstm=105.06891632080078
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
reset W, x , Y, state
state is None = True
sum_loss:sgd=966.5319213867188,rms=277.1605224609375,adam=143.6751251220703,lstm=109.35062408447266
(以上代码在一个文件里面执行。复制粘贴格式代码好像需要Chrome或者IE浏览器打开才行???)
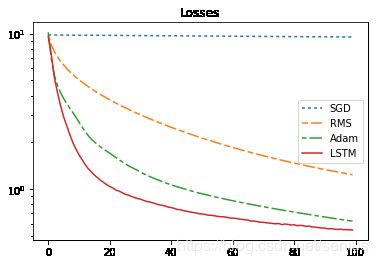
可以看到:SGD 优化器对于这个问题已经不具备优化能力,RMSprop优化器表现良好,Adam优化器表现依旧突出,LSTM优化器能够媲美甚至超越Adam(Adam已经是业界认可并大规模使用的优化器了)
请注意,LSTM优化器的最终优化策略是没有任何人工设计的经验在里面,是自动学习出的一种学习策略!并且这种方法理论上可以应用到任何优化问题
换一个角度讲,针对给定的优化问题,LSTM可以逼近或超越现有的任何人工优化器,不过对于大型的网络和复杂的优化问题,这个方法的优化成本太大,优化器性能的稳定性也值得考虑,所以这个工作的创意是独特的,实用性有待考虑~~
以上代码参考Deepmind的Tensorflow版本,遵照论文思路,加上个人理解,力求最简,很多地方写得不够完备,如果有问题,还请多多指出!
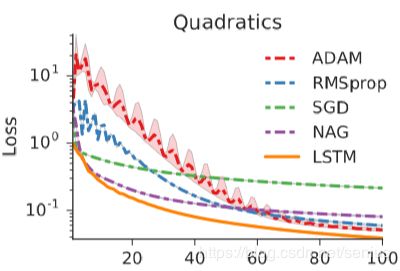
上图是论文中给出的结果,作者取最好的实验结果的平均表现(试出了最佳学习率?)展示,我用下面和论文中一样的实验条件(不过没使用NAG优化器),基本达到了论文中所示的同样效果?性能稳定性较差一些
(我怀疑论文的实验Batchsize不是代码中的128?又或者作者把batchsize当作函数的随机采样?我这里把batchsize当作确定的参数,随机采样单独编写)。
实验条件:
-
PyTorch-0.4.1 cpu
-
优化问题为Quadratic函数:
-
W : [128,10,10] Y: [128 , 10] x: [128, 10] 从IID的标准Gaussian分布中采样,初始 x = 0
-
全局优化器optimizer使用Adam优化器, 学习率为0.1(或许有更好的选择,没有进行对比实验)
-
CoordinateWise LSTM 使用LSTM_Optimizee_Model:
- (lstm): LSTM(10, 20, num_layers=2)
- (Linear): Linear(in_features=20, out_features=10, bias=True)
-
未使用任何数据预处理(LogAndSign)和后处理
-
UnRolled Steps = 20 Optimizee_Training_Steps = 100
-
*Global_Traing_steps = 1000 原代码=10000,或许进一步优化LSTM优化器,能够到达更稳定的效果。
-
另外,原论文进行了mnist和cifar10的实验,本篇博客没有进行实验,代码部分还有待完善,还是希望读者多读原论文和原代码,多动手编程实验!
def learn():
return "知识"
def learning_to(learn):
print(learn())
return "学习策略"
print(learning_to(learn))
人可以从自身认识与客观存在的差异中学习,来不断的提升认知能力,这是最基本的学习能力。而另一种潜在不容易发掘,但却是更强大的能力–在学习中不断调整适应自身与外界的学习技巧或者规则–其实构建了我们更高阶的智能。比如,我们在学习知识时,我们总会先接触一些简单容易理解的基本概念,遇到一些理解起来困难或者十分抽象的概念时,我们往往不是采取强行记忆,即我们并不会立刻学习跟我们当前认知的偏差非常大的事物,而是把它先放到一边,继续学习更多简单的概念,直到有所“领悟”发现先前的困难概念变得容易理解
心理学上,元认知被称作反省认知,指人对自我认知的认知。弗拉威尔称,元认知是关于个人自己认知过程的知识和调节这些过程的能力:对思维和学习活动的知识和控制。那么学会适应性地调整学习策略,也成为机器学习的一个研究课题,a most ordinary problem for machine learning is that although we expect to find the invariant pattern in all data, for an individual instance in a specified dataset,it has its own unique attribute, which requires the model taking different policy to understand them seperately .
以上均为原创,转载请注明来源
https://blog.csdn.net/senius/article/details/84483329
or https://yangsenius.github.io/blog/LSTM_Meta/
溜了溜了
[点我]下载代码: learning_to_learn_by_pytorch.py
Github地址,微小改动及更新
简单直观地理解,请看伪代码:
simple_learning_to_learn.py
参考:
1.Learning to learn by gradient descent by gradient descent
2. Learning to learn in Tensorflow by DeepMind
3.learning-to-learn-by-gradient-descent-by-gradient-descent-4da2273d64f2