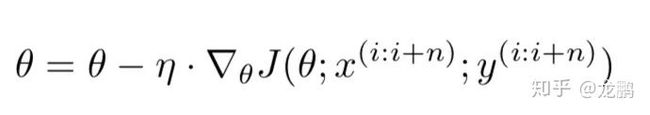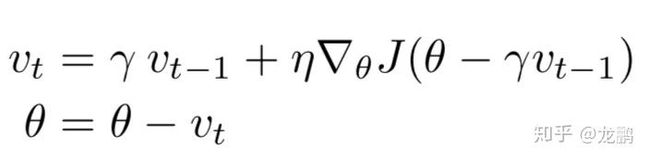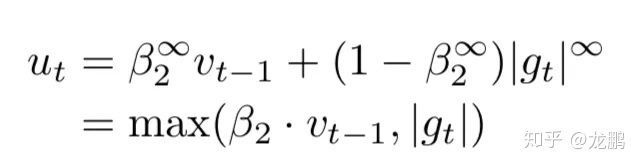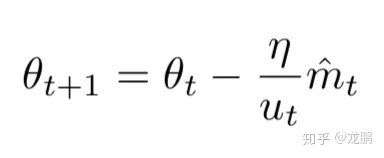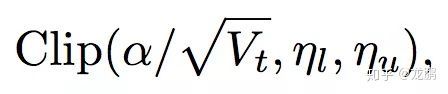机器学习各类优化算法总结
目录
1 Intro
2 一阶优化算法
2.1 Gradient descent
Batch Gradient Descent
Stochastic Gradient Descent
Mini-batch Gradient Descent
2.2 Momentum
2.3 Nesterov accelerated gradient (NAG)
2.4 AdaGrad
2.5 Adadelta与Rmsprop
2.6 Adam
2.7 AdaMax
2.8 Nadam
2.9 AMSgrad
2.10 Adafactor
2.11 Adabound
3 二阶优化算法
3.1 牛顿法
3.2 拟牛顿法
Conclusion
Reference
1 Intro
深度学习模型的优化是一个非凸优化问题,这是与凸优化问题对应的。
对于凸优化来说,任何局部最优解即为全局最优解。用贪婪算法或梯度下降法都能收敛到全局最优解。而非凸优化问题则可能存在无数个局部最优点,损失曲面如下,可以看出有非常多的极值点,有极大值也有极小值。
除了极大极小值,还有一类值为“鞍点”,简单来说,它就是在某一些方向梯度下降,另一些方向梯度上升,形状似马鞍,如下图红点就是鞍点。
对于深度学习模型的优化来说,鞍点比局部极大值点或者极小值点带来的问题更加严重。
目前常用的优化方法分为一阶和二阶,这里的阶对应导数,一阶方法只需要一阶导数,二阶方法需要二阶导数。
常用的一阶算法就是:随机梯度下降SGD及其各类变种了。
常用的二阶算法就是:牛顿法等。
2 一阶优化算法
2.1 Gradient descent
Batch Gradient Descent
Stochastic Gradient Descent
Mini-batch Gradient Descent
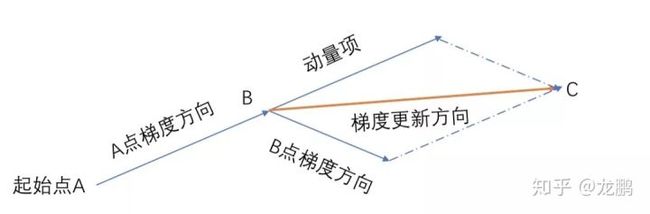
2.2 Momentum
前面说了梯度下降算法是按照梯度的反方向进行参数更新,但是刚开始的时候梯度不稳定呀,方向改变是很正常的,梯度就是抽疯了似的一下正一下反,导致做了很多无用的迭代。
而动量法做的很简单,相信之前的梯度。如果梯度方向不变,就越发更新的快,反之减弱当前梯度。
- 优点:可以使得梯度方向不变的维度上速度变快,梯度方向有所改变的维度上的更新速度变慢,这样就可以加快收敛并减小震荡。
- 缺点:这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚,如果它能具备一些先知,例如快要上坡时,就知道需要减速了的话,适应性会更好。
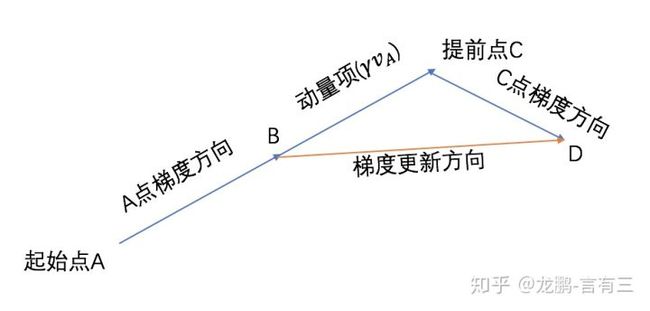
2.3 Nesterov accelerated gradient (NAG)
仍然是动量法,只是它要求这个下降更加智能。
既然动量法已经把前一次的梯度和当前梯度融合,那何不更进一步,直接先按照前一次梯度方向更新一步将它作为当前的梯度,看下面的式子就明白了。
2.4 AdaGrad
前面的一系列优化算法有一个共同的特点,就是对于每一个参数都用相同的学习率进行更新。但是在实际应用中各个参数的重要性肯定是不一样的,所以我们对于不同的参数要动态的采取不同的学习率,让目标函数更快的收敛。
adagrad方法是将每一个参数的每一次迭代的梯度取平方累加再开方,用基础学习率除以这个数,来做学习率的动态更新。【这样每一个参数的学习率就与他们的梯度有关系了,那么每一个参数的学习率就不一样了!也就是所谓的自适应学习率】
- 优点:减少了学习率的手动调节
- 缺点:分母会不断积累,这样学习率就会收缩并最终会变得非常小。
2.5 Adadelta与Rmsprop
![]()
RMSprop方法的不同就在于分子上还是使用学习率η而不是Adadelta中的RMS
![]()
2.6 Adam
Adam对梯度的一阶和二阶都进行了估计与偏差修正,使用梯度的一阶矩估计和二阶矩估计来动态调整每个参数的学习率。
2.7 AdaMax
将Adam使用的二阶矩变成更高阶,就成了Adamax算法。
2.8 Nadam
Nag加上Adam,就成了Nadam方法,即带有动量项的Adam。
![]()
2.9 AMSgrad
ICLR 2018最佳论文提出了AMSgrad方法,研究人员观察到Adam类的方法之所以会不能收敛到好的结果,是因为在优化算法中广泛使用的指数衰减方法会使得梯度的记忆时间太短。
在深度学习中,每一个mini-batch对结果的优化贡献是不一样的,有的产生的梯度特别有效,但是也一视同仁地被时间所遗忘。
具体的做法是使用过去平方梯度的最大值来更新参数,而不是指数平均。
2.10 Adafactor
Adam算法有两个参数,beta1和beta2,相关研究表明beta2的值对收敛结果有影响,如果较低,衰减太大容易不收敛,反之就容易收敛不稳定。Adafactor是通过给beta1和beta2本身也增加了一个衰减。
beta2的值刚开始是0,之后随着时间的增加而逼近预设值。
2.11 Adabound
上面说了,beta2的值造成Adam算法有可能不收敛或者不稳定而找不到全局最优解,落实到最后的优化参数那就是不稳定和异常(过大或者过小)的学习率。Adabound采用的解决问题的方式就非常的简单了,那就是限制最大和最小值范围,约束住学习率的大小。
ηl(t)和ηu(t)分别是一个随着时间单调递增和递减的函数,最后两者收敛到同一个值。
3 二阶优化算法
二阶的方法因为使用了导数的二阶信息,因此其优化方向更加准确,速度也更快,这是它的优势。
但是它的劣势也极其明显,使用二阶方法通常需要直接计算或者近似估计Hessian 矩阵,一阶方法一次迭代更新复杂度为O(N),二阶方法就是O(N*N),深层神经网络中变量实在是太多了,搞不动的。
3.1 牛顿法
待完善
3.2 拟牛顿法
待完善
Conclusion
![]()
![]()
![]()
Reference
【AI初识境】为了围剿SGD大家这些年想过的那十几招(从momentum到Adabound)
深度学习总结(一)各种优化算法