算法设计与分析 0-1背包问题 动态规划解法【超详细】

0-1背包问题 问题描述

给定i个物品和一个容量为的背包，物品的重量是Wi，其价值为Vi
物品个数为i，背包容量为C。
如何选择装入背包内的物品，使得装入背包中的物品的总价值最大？

其中，每种物品只有全部装入背包或不装入背包两种选择。
物品不能分割，不能重复使用。

动态规划算法思路

首先建立一个数组B[i][c]，最上面一行表示背包容量，最左边一列表示物品编号，中间填充的数值表示当当前背包容量为C，当前被考虑的物品编号为k的情况下，做出最优决定时产生的背包价值。

如下图所示：（不用关心图中数据，理解整体结构含义即可）

实例分析

已知背包的容量为20，并给定5种物品，其重量和价值如下图所示：

令B(k,w)表示在前k个物品中能够装入容量为的背包中时，背包总价值的最大值。

得到如下动态函数：

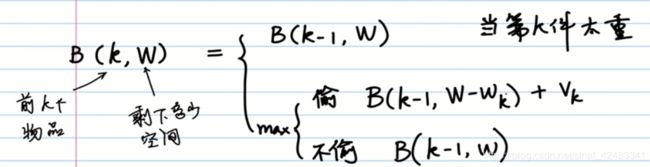
利用上述函数，一行一行填表即可。
填表顺序为：先从左上角开始，填第一行，第二行，…一直到结束，并不需要递归。
右下角即背包可装下的最大价值26

详细分析 疑难解答

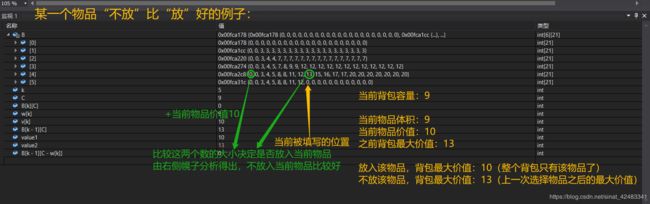
可能有人会问，“当判断一个物品k是否应该装入背包的时候，难道不是只要能装进去，就应该装进去，这样才是最优吗”？

对于这个问题，我的理解是：

不一定非要装进去当前能装进去的物品。如果当前物品能装进去，那么：

• 放入第k件物品后，背包总价值 = 先给这件物品留出空间，剩余的背包大小能装进的最大价值 + 这件物品的价值
• 不放入第k件物品，背包总价值 = 不用给这件物品留出空间，当前背包大小能装进的最大价值(就是判断完上一件物品之后背包的价值)

说白了，就是当当前物品又大又轻时，虽然可以把它装进去，但是在给它留出空间的同时，浪费了背包的容量。还不如不装当前物品，而去选择其他物品装入。

那么这个“其他物品”指什么呢？就是在判断这个物品该不该装之前，已经计算过的当前背包容量下，可以将前k-1件物品放入或不放入时，背包的最大价值。

如下图，这是某一个物品“不放”比“放”好的例子：

用C代码实现后，应该更容易理解一些（不懂的话请看注释，重点在注释）：

	//填表过程
	for (k = 1; k < N; k++)
	{
		for (C = 1; C < W; C++)
		{
			if (w[k] > C)								//第k件物品放不进去 此时背包的价值 = 判断完上一件物品之后背包的价值
			{
				B[k][C] = B[k - 1][C];
			}
			else
			{
				int value1 = B[k - 1][C - w[k]]+v[k];	//放入第k件物品后 背包总价值 = 先给这件物品留出空间，剩余的背包大小能装进的最大价值 + 这件物品的价值
				int value2 = B[k - 1][C];				//不放入第k件物品 背包总价值 = 不用给这件物品留出空间，当前背包大小能装进的最大价值(就是判断完上一件物品之后背包的价值)

				if (value1 > value2)
				{
					B[k][C] = value1;
				}
				else
				{
					B[k][C] = value2;
				}
			}
		}
	}

逆推装入的物品

计算出矩阵以及最大可装价值之后，如何逆推装入的物品？
如下图，从右下角开始，向上层层逆推。

• 如果上下数字相同，说明这个物品未被放入背包。
• 如果上下数字不同，说明这个物品已被放入背包，此时计算放入此物品之前背包剩余容量，并找出上一行对应位置。

附录

我的笔记

运行结果
前几行输出为：某一个物品“不放”比“放”好的情况，可以无视
后面的矩阵才是最终的运算结果

完整代码 C++

#include
#include
#define N 6		//物品的个数
#define W 21	//背包容量

int B[N][W] = { 0 };
int w[6] = { 0,2,3,4,5,9 };	//物品重量
int v[6] = { 0,3,4,5,8,10 };//物品价值

void knapsack()
{
	int k;	//第K个物品
	int C;	//背包剩余重量

	//填表
	for (k = 1; k < N; k++)
	{
		for (C = 1; C < W; C++)
		{
			if (w[k] > C)								//第k件物品放不进去 此时背包的价值 = 判断完上一件物品之后背包的价值
			{
				B[k][C] = B[k - 1][C];
			}
			else
			{
				int value1 = B[k - 1][C - w[k]] + v[k];	//放入第k件物品后 背包总价值 = 先给这件物品留出空间，剩余的背包大小能装进的最大价值 + 这件物品的价值
				int value2 = B[k - 1][C];				//不放入第k件物品 背包总价值 = 不用给这件物品留出空间，当前背包大小能装进的最大价值(就是判断完上一件物品之后背包的价值)

				if (value1 > value2)
				{
					B[k][C] = value1;
				}
				else
				{
					B[k][C] = value2;
					if (value1 < value2)printf("k=%d C=%d\n", k, C);
				}
			}
		}
	}
}
int main()
{
	knapsack();
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < W; j++)
		{
			printf("%4d ", B[i][j]);
		}
		printf("\n\n");
	}
	system("pause");
}