机器学习中的高斯过程简介

本文符号的意义

$X$: 训练样本集输入特征
$y$: 训练样本对应的输出值
$X_{\ast }$：待预测样本点输入特征
$y_{\ast }$：带预测样本点的预测值
$K$: 核函数
${\theta }_i$：核函数的参数
$m$: 均值向量
$\Sigma$: 协方差阵
$d$: 表征样本之间的相似度，$d=X-X^{\prime }$
$\mathcal{N}$:高斯分布函数
$\Phi$: 累积高斯分布函数

核心思想

输出$y$服从多维高斯分布，特征$X$估计多维高斯分布参数。
GPR :核函数估计$\Sigma$，构建$y_{\ast }与y$的联合高斯分布，进而计算得到$y_{\ast }$的条件概率分布，均值即为预测值，方差即为不确定性估计。
GPC : probabilistic classification，采用logistic函数"squash"隐藏变量$f$(服从高斯分布)，然后积分求得概率值。

预备知识

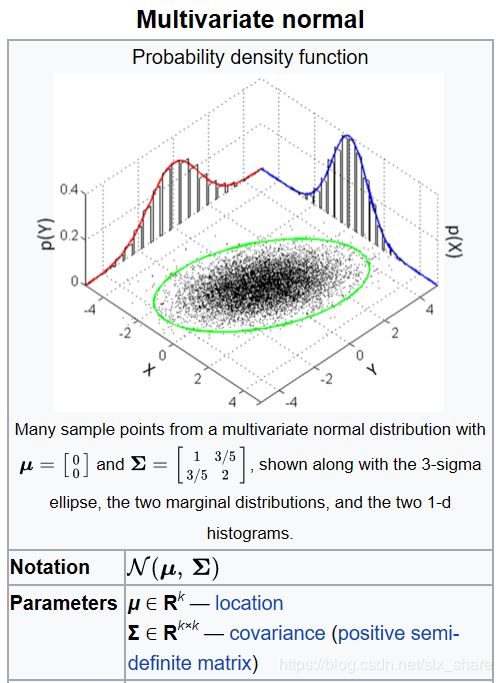
多维高斯分布

多维高斯分布含有两个重要的参数：
均值向量 ：均值向量不影响函数形态。
协方差阵 ：各个维度上变量间协方差阵决定了函数的形态。
多维高斯分布表达式如下($\mu 为各个变量均值构成的均值向量，\Sigma 为协方差阵$):

(图片摘自维基百科)

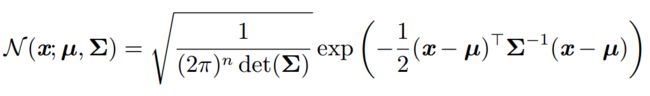
随机过程

随机变量随时间改变的过程称为随机过程。这里的时间泛指过程涉及的所有参数。从动态角度看，一个n维随机变量就是一个随机过程。例如，依次掷6次色子，得到的点数$[X1,X2,X3,X4,X5,X6]$(考虑样本二重性，在没有观测时就是随机变量)，这就是一次随机过程，该过程的参数就是时间序列$T=[0,1,2,3,4,5,6]$(只要点数与时间参数对应即可，可以无序)。一次随机过程产生的观测值(例如$[1,3,5,2,1,3,6$)称之为样本向量。总之，一个样本的产生需要先指定参数，获取统计分布函数，最终生成观测值集合。
据此，给出随机过程的定义如下：
样本空间$\Omega =\{\omega \}$,参数集$T\in (-\infty ,+\infty )$,如果对于任意$t\in T$,存在随机变量$X(\omega ,t)$,那么随机变量构成的簇$\{X(\omega ,t),t\in T\}$(随机变量的集合)就是一个随机过程。

高斯过程

高斯过程就是一个随机过程。随机变量就是$y$，样本空间就是$y$的取值范围。$y$的集合就是一个随机过程。在这个随机过程中，随机变量服从多维高斯分布，相应的参数集$T$就是$(m,\Sigma )$可以表示为:$$\begin{gathered} y=f(X)+\mathcal{N}(0,{\sigma }_n^2) \\ f(X)=g(m(X),K(X)) \end{gathered}$$其中，$f(X)$就是一个特定的多维高斯分布，$N(0,{\sigma }_n^2)$是噪音项，$m(X)$是高斯分布的均值向量，通常在机器学习中设置为零向量。$\Sigma$用核函数$K(X)$估计，因此实际模型的超参数主要是核函数的参数$\{{\theta }_i\}$。

核函数

核函数用来估计多维高斯分布的协方差阵，需要设定初始超参数。高斯过程是根据$X与X_{\ast }$的相似度来获取$y与y_{\ast }$的联合分布的，而核函数决定了如何衡量相似度。一方面，基于对样本间相似性的理解，选择合适的核函数，例如存在周期性可选用ExpSineSquared 核函数；另一方面，可以对相似性进行分解，对不同的相似性采用不同的核函数，然后对核函数进行组合，例如可将相似性拆分为总体以及局部两方面等。

常用的核函数

(图片摘自维基百科)
可以发现，大多数核函数均含有一个超参数$l$，称为length_scale，用以控制smoothness

特点

stationary：核函数的取值仅取决于$d$，与具体的$X$值无关。显然线性核函数是non-stationary
isotropy：核函数取值仅取决于$|d|$，而与$d$的方向无关。
smoothness：直观地理解就是核函数值对$|d|$越敏感，smoothness越小
Periodicity：核函数是周期性函数
一个核函数同时满足stationary以及isotropy，则称函数是homogeneous，这类核函数使用较多。

高斯过程回归(GPR)

训练

训练的目的就是获得核函数的参数。
预先设定的核函数参数$\{{\theta }_i\}$显然是不够准确的，需要根据样本的信息对参数进行调节，得到后验高斯过程。采用极大似然估计的方法求解核函数的参数。最大化对数边缘似然函数(LML)：$$L=logp(y\mid x,{\theta }_i)=-\frac{1}{2}log\mid \sum \mid -\frac{1}{2}(y-\mu ){}^T\sum {}^{-1}(y-\mu )-2nlog(2\pi )$$(注：参考机器学习中的高斯过程的推导)

预测

假设待预测的样本有$n_{\ast }$个，$n_{\ast }个y_{\ast }$来自$n_{\ast }$维高斯分布。假设训练数据集中有$n个y$，来自于$n$维高斯分布。根据高斯分布的可加性,$\left(\begin{array}{c}y\\ y_{\ast }\end{array}\right)$服从$n+n_{\ast }$维高斯分布。我们的目的就是根据$n+n_{\ast }$维高斯分布（$\left(\begin{array}{c}y\\ y_{\ast }\end{array}\right)$的联合概率分布)获得$y_{\ast }$的值。这个时候，各个样本的特征向量$X_i(包括X_{\ast })$派上用场了：$$\begin{gathered} \left(\begin{array}{c}y\\ y_{\ast }\end{array}\right)\to \mathcal{N}(0,\Sigma ) \\ \Sigma =\left(\begin{array}{cc}K& K_{\ast }\\ K_{\ast }^T& K_{\ast \ast }\end{array}\right) \end{gathered}$$其中，$K由X计算，K_{\ast }由X和X_{\ast }计算得到，K_{\ast \ast }由X_{\ast }计算得到$。然后，求得$y_{\ast }$的条件概率分布如下：$$\begin{gathered} p(y_{\ast }|X_{\ast },X,y)=N(y_{\ast }|{\mu }_{\ast },{\Sigma }_{\ast }) \\ {\mu }_{\ast }=K_{\ast }^T{K}^{-1}y \\ {\Sigma }_{\ast }=K_{\ast \ast }-K_{\ast }^T{K}^{-1}{K}_{\ast } \end{gathered}$$其中，${\mu }_{\ast }就是n_{\ast }预测值y_{\ast }构成的均值向量，{\Sigma }_{\ast }则代表了预测的不确定性$

高斯过程分类(GPC)

回归与分类的本质是一致的。我们同样可以进行回归分析，然后采用Sigmoid函数将回归预测值转化为概率值(英文文献通常用"squash"形容这一过程，即将预测值压缩到[0,1]区间)，最后通过概率判别所属类即可。例如逻辑斯蒂回归就是先采用线性回归，然后采用logistic函数进行"squash"。逻辑斯蒂回归模型可表示如下$$p(y|X)=\frac{1}{1+e^{-yf(X)}}$$其中，$y\in \{1,-1\}$。$f(X)=wX$。先给出初始$w=I$，经过训练得到后验的$w$。

训练

高斯过程与逻辑斯蒂回归类似，同样采用logistic函数进行"squash"，只不过将线性回归模型改为先验高斯函数$f(X)=\mathcal{N}(0,K(X))$，先给出初始核函数参数$\theta$，经过训练后获得后验最优的核函数超参数。训练过程同GPR，即最大化对数边缘似然函数。

预测

首先获得待预测样本对应的$f$的多维高斯分布(后验分布)，不用关心隐藏变量$f$的值，在后续积分中会消除。这不同于逻辑回归，需要计算出线性回归值。即

式中，f为训练样本对应的隐藏变量。积分求得概率值，即

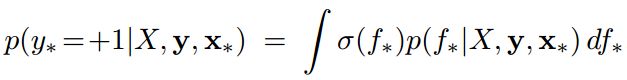
式中，$\sigma$即为logistic函数。积分结果为$$p(y_{\ast }=+1)=\Phi (\frac{{\mu }_{\ast }}{\sqrt{1+{\sigma }_{\ast }^2}})$$其中${\mu }_{\ast },{\sigma }_{\ast }$分别为待预测点对应的均值以及标准差(均值向量以及协方差矩阵的计算同GPR)。

多分类

当用于多分类时，采取的方式与支持向量机多分类方式一致，即"one VS rest"和"one VS one"。注意，采用"one VS one"方式时，n个类的多分类问题的核函数有$C_n^2$个。

Tikhonov正则化

当数据中存在噪声时，为防止过拟合需要进行Tikhonov正则化，即协方差阵的对角元素加上参数alpha(噪声水平)，另一种替代方式是在原有核函数基础上加一个WhiteKernel。

优缺点

优点

• 给出预测值的概率，给出置信区间
• 可以个人定制核函数形式

缺点

• 不稀疏，训练过程需要用到所有的样本以及特征
• 高维情况下效率低，尤其当维度超过几十个时

为什么用核函数计算协方差矩阵？

高斯过程的各个变量$y$间是互相联系的，这种联系体现在协方差阵上，我们也是利用待预测点与样本点间的联系来得到预测值的。
假设不用核函数(也就是不使用$y$对应的特征)没办法得到各个样本点间的协方差，协方差矩阵除对角线元素外全部为零，导致自变量$y$之间毫无联系。
例如(参考资料1中举的例子，这里重写一下代码)：

import matplotlib.pyplot as plt
import numpy as np
from itertools import cycle

color_cycle = cycle('kbryg')
n_variable = 20
n_sample = 5

plt.figure(figsize=(500, 300))
sigma_s = np.eye(n_variable) # 协方差阵为对角矩阵

for _ in range(n_sample):
    point = np.random.multivariate_normal(np.zeros(n_variable), sigma_s)
    plt.plot(np.arange(n_variable), point, color=next(color_cycle))
    plt.scatter(np.arange(n_variable), point)

plt.rcParams['font.sans-serif'] = ['SimHei']  # 正确显示中文
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号
plt.title('不使用核函数的情况', fontsize=24)
plt.xticks(np.arange(n_variable))
plt.xlabel('y', fontsize=20)
plt.show()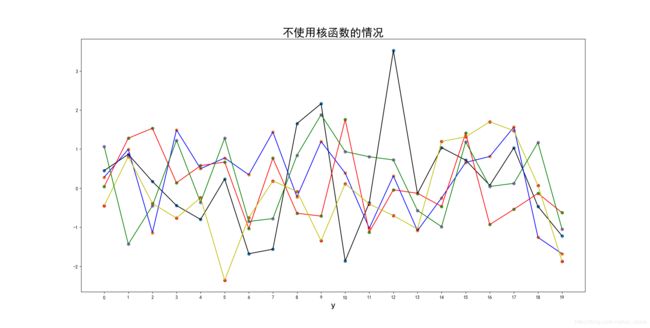

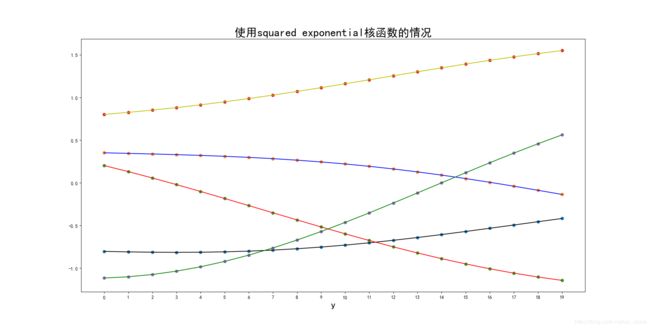
核函数来估计协方差，能很好反映各个变量$y$间的关系。因为核函数充分考虑了样本间的相似性(大多用$d$度量)。
例如采用squared exponential核函数后，曲线变得平滑了：

xs = np.linspace(0, 1, n_variable)  # 构建y对应的特征
sigma_s = np.exp(-(np.expand_dims(xs, axis=0) - np.expand_dims(xs, axis=1)) ** 2 / 2)  # 依据特征xs构建协方差阵

代码

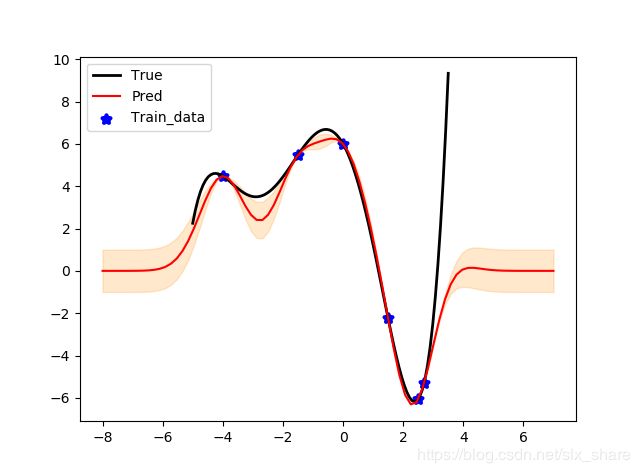
重构参考资料1中GPR的示例代码。

import numpy as np
from scipy.optimize import minimize
from scipy.spatial.distance import pdist, cdist, squareform


class Kernel:
    # RBF核函数
    def __init__(self, theta):
        self.theta = theta

    def __call__(self, X, Y=None):
        if Y is None:
            dists = pdist(X / self.theta, metric='sqeuclidean')
            K = np.exp(-0.5 * dists)
            K = squareform(K)
            np.fill_diagonal(K, 1)
        else:
            dists = cdist(X / self.theta, Y / self.theta, metric='sqeuclidean')
            K = np.exp(-0.5 * dists)
        return K


class GPR:
    def __init__(self):
        self.K = None
        self.X = None
        self.y = None

    def log_marginal_likelihood(self, theta):
        # 计算对数边缘似然函数
        K = Kernel(theta)
        sigma = K(self.X)
        log_likelihood = np.log(np.linalg.det(sigma)) + \
                         self.y @ np.linalg.inv(sigma) @ self.y + \
                         sigma.shape[0] * np.log(2 * np.pi)
        return - 0.5 * log_likelihood

    def fit(self, X, y):
        # 训练，获取核函数最优参数
        self.X = X
        self.y = y

        def obj_func(theta):
            return - self.log_marginal_likelihood(theta)

        theta_opt = minimize(obj_func, np.array([1.0]), method='BFGS')
        self.K = Kernel(theta_opt.x[0])

    def predict(self, X_pred):
        # 预测，获取y*的条件概率分布
        K_pred = self.K(X_pred)
        K_train = self.K(self.X)
        K_pred_train = self.K(self.X, X_pred)
        K_inv = np.linalg.inv(K_train)
        mu = K_pred_train.T @ K_inv @ self.y
        sigma = K_pred - K_pred_train.T @ K_inv @ K_pred_train
        return mu, np.diagonal(sigma)


if __name__ == '__main__':
    import matplotlib.pyplot as plt

    gpr = GPR()

    # 生成样本数据
    coefs = [6, -2.5, -2.4, -0.1, 0.2, 0.03]


    def f(x):
        total = 0
        for exp, coef in enumerate(coefs):
            total += coef * (x ** exp)
        return total


    xs = np.linspace(-5.0, 3.5, 100)
    ys = f(xs)

    X_train = np.array([-4, -1.5, 0, 1.5, 2.5, 2.7])
    y_train = f(X_train)

    X_train = X_train.reshape(-1, 1)
    X_pred = np.linspace(-8, 7, 80).reshape((-1, 1))

    gpr.fit(X_train, y_train)
    y_pred, y_std = gpr.predict(X_pred)

    plt.plot(xs, ys, color='k', linewidth=2, label='True')
    plt.scatter(X_train, y_train, color='b', marker='*', linewidths=3, label='Train_data')
    plt.plot(X_pred, y_pred, color='r', label='Pred')

    plt.fill_between(X_pred.reshape(1, -1)[0], y_pred - y_std, y_pred + y_std, color='darkorange',
                     alpha=0.2)
    plt.legend()
    plt.show()

结果如图所示：

参考资料

1. http://bridg.land/posts/gaussian-processes-1
2. http://www.datalearner.com/blog/1051459170229238
3. https://en.wikipedia.org/wiki/Gaussian_process
   注：如有不当之处，请指正。