用频域最小误差平方方法设计线性相位FIR低通数字滤波器

一、概述：

1. 数字滤波器
数字滤波器是指输入、输出均为数字信号，通过一定运算关系改变输入信号所含频率成分的相对比例，或者滤除某些频率成分的器件。

数字滤波器是一个离散时间系统（按预定的算法，将输入离散时间信号转换为所要求的输出离散时间信号的特定功能装置）。应用数字滤波器处理模拟信号时，首先须对输入模拟信号进行限带、抽样和模数转换。

与模拟滤波器相比，数字滤波器的优点是：
（1） 精度和稳定性高；
（2） 系统函数容易改变，所以灵活性高；
（3） 不要求阻抗匹配；
（4） 便于大规模集成。

数字滤波器有低通、高通、带通、带阻和全通等类型。它可以是时不变的或时变的、因果的或非因果的、线性的或非线性的。应用最广的是线性、时不变数字滤波器，以及FIR滤波器。

数字滤波器包括有限长脉冲响应滤波器（FIR filter）和无限长滤波器（IIR filter），它们的系统函数分别为：

2.FTR滤波器
FIR滤波器：有限长单位冲激响应滤波器，是数字信号处理系统中最基本的元件，它可以在保证任意幅频特性的同时具有严格的线性相频特性，同时其单位抽样响应是有限长的，因而滤波器是稳定的系统。因此，FIR滤波器在通信、图像处理、模式识别等领域都有着广泛的应用。

有限长单位冲激响应（FIR）滤波器有以下特点：
(1) 系统的单位冲激响应h (n)在有限个n值处不为零；
(2) 系统函数H(z)在|z|>0处收敛，极点全部在z = 0处（因果系统）；
(3) 结构上主要是非递归结构，没有输出到输入的反馈，但有些结构中（例如频率抽样结构）也包含有反馈的递归部分。

---

二、设计方法

1、计算滤波器的系数

设N-1阶FIR数字滤波器的单位冲激响应为h(n)，则传递函数H(z)为
.FIR数字滤波器的实际幅度响应H(ω)与理想幅度响应Hd(ω)的误差函数定义为.

根据帕塞瓦定理，误差函数可以表示为:

其中M=(N-1)/2。该式表明，若要使E最小，必须选择h(n)，使它与hd(n)对应的N个值相等，即h(n)= hd(n) ， -M≤n≤M
为了减少吉伯斯(Gibbs)效应（Gibbs 现象就是理想滤波器的单位脉冲响应hd[k]截断获得的 FIR 滤波器的幅度函数 A(Ω) 在通带和阻带都呈现出振荡现象），通常在通带与阻带之间加一个过渡带（fc≤f≤fs）。过渡带函数常采用P阶样条函数，此时滤波器的系数为
， （0≤n≤N-1）

过渡带函数也可采用升余弦函数．此时滤波器的系数为
， （0≤n≤N-1）

2、计算滤波器频率响应

数字滤波器的频率响应H（w）为：
，

即 ，
其中|H（w）|是数字滤波器的幅频响应，若用分贝表示，则用。数字滤波器的相频响应为：。

---

三、程序源码

设计一个20阶的FIR低通数字滤波器，其通带边界频率为0.2，阻带边界频率为0.3，采用一阶样条函数作为过渡带。选择参数: 采样频率=l，tp=1。

C++部分（vs2013）：

#define _CRT_SECURE_NO_DEPRECATE
#include
#include
#include
#include
#include
#include


using namespace std;
/*
  b[m+1]-->存放滤波器分子多项式的系数
  a[n+1]-->存放滤波器分母多项式的系数
  m-->滤波器分子多项式的阶数
  n-->滤波器分母多项式的阶数
  x[len]-->当sign=0时，存放滤波器频率响应的实部Re[H(w)];当sign=1时，存放滤波器幅频响应|H(w)|；当sigh=2时，存放用分贝表示的滤波器幅频响应|H(w)|
  y[len]-->当sign=0时，存放滤波器频率响应的虚部lm[H(w)];当sign=1或sigh=2时，存放滤波器的相频响应ψ(w)
  len-->频率响应的长度
  sign-->当sign=0时，计算滤波器频率响应的实部Re[H(w)]和虚部lm[H(w)]；当sign=1时，计算存放滤波器幅频响应|H(w)|和相频响应ψ(w)；
  当sign=2时，计算存放滤波器幅频响应|H(w)|（用dB表示）和相频响应ψ(w)
  */


//计算滤波器频率响应
void gain(double b[], double a[], int m, int n, double x[], double y[], int len, int sign){
    int i, k;
    double temp;
    double ar, ai, br, bi, zr, zi, im, re, den, numr, numi, freq, tem;
    for (k = 0; k < len; k++){
        freq = k * 0.5 / (len - 1);
        zr = cos(-8.0 * atan(1.0) * freq);
        zi = sin(-8.0 * atan(1.0) * freq);
        br = 0.0;
        bi = 0.0;
        for (i = m; i>0; i--){
            re = br;
            im = bi;
            br = (re + b[i]) * zr - im * zi;
            bi = (re + b[i]) * zi + im * zr;
        }
        ar = 0.0;
        ai = 0.0;
        for (i = n; i > 0; i--){
            re = ar;
            im = ai;
            ar = (re + a[i])*zr - im * zi;
            ai = (re + a[i]) * zi + im * zr;
        }
        br = br + b[0];
        ar = ar + 1.0;
        numr = ar * br + ai * bi;
        numi = ar * bi - ai * br;
        den = ar * ar + ai * ai;
        x[k] = numr / den;
        y[k] = numi / den;
        switch (sign){
        case 1:
            temp = sqrt(x[k] * x[k] + y[k] * y[k]);
            y[k] = atan2(y[k], x[k]);
            x[k] = temp;
            break;
        case 2:
            temp = x[k] * x[k] + y[k] * y[k];
            y[k] = atan2(y[k], x[k]);
            x[k] = 10.0 * log10(temp);
        }
    }
}

//计算滤波器函数的系数，并存入h[]
void firls(int n, double fc, double fs, int tp, double h[]){
    double fq, fr;
    //声明两个子程序，my_ls(),my_wgt()
    void my_ls(double h[], int n, double fc);
    void my_wgt(double h[], int& n, int& tp, double& fq);
    fq = fs - fc;
    fr = fs + fc;
    my_ls(h, n, fr);
    my_wgt(h, n, tp, fq);
}

void my_ls(double h[], int n, double fr){
    int i, m, n2;
    double q, am, pi;
    pi = 4.0*atan(1.0);
    m = n / 2;
    am = n / 2.0;
    n2 = (n - 1) / 2;
    if (m == am)
        h[m] = fr;
    for (i = 0; i <= n2; i++){
        q = pi*(i - am);
        h[i] = sin(fr*q) / q;
    }

}

void my_wgt(double h[], int& n, int& tp, double& fq){
    int i;
    double q, am, pi, ql, wt;
    pi = 4.0*atan(1.0);
    q = pi*fq;
    am = n / 2.0;
    if (fq == 0.0) 
        return;
    if (tp != 0){
        for (i = 0; ipow(sin(ql) / ql, tp);
            h[i] = wt*h[i];
        }

    }
    else{
        for (i = 0; icos(q*(i - am));
            if (fabs(wt)>1.0e-6){
                wt = wt / (1 - pow((2 * fq*(i - am)), 2));
            }
            else{
                wt = pi / 4.0;
            }
            h[i] = wt*h[i];
        }

    } 

    for (i = 0; i/*
  n: 滤波器的阶数
  f: 采样频率
  fc: 通带边界频率
  fs: 阻带边界频率
  tp: 样条函数的阶数
  fname: 幅频响应文件名
  h[]: 存放滤波器函数的系数
*/


void test(){
    int i, j, n, n2, tp;
    double f, fc, fs, freq;
    double h[100], c[100], x[300], y[300];
    c[1] = 0.0;
    ofstream table;
    //依次输入实验所需数据
    cout << "请输入滤波器的阶数"<cin >> n;
    cout << "请输入通带边界的频率" << endl;
    cin >> fc;
    cout << "请输入阻带边界的频率" << endl;
    cin >> fs;
    cout << "请输入采样频率" << endl;
    cin >> f;
    fc = fc / f;
    fs = fs / f;
    cout << "请输入样条函数的阶数" << endl;
    cin >> tp;
    //调用
    firls(n, fc, fs, tp, h);
    n2 = n / 2;
    table.open("F:\\FIR\\FIR\\keshe.txt");
    //依次输出滤波器函数的系数
    for (i = 0; i <= n2; i++){
        j = n - i;
        cout << "h" << i << "=" << h[i] << "= h" << j << endl;
    }
    //进行计算滤波器频率响应
    gain(h, c, n, 1, x, y, 300, 2);
    //将实验数据依次写入keshe文本文件
    for (i = 0; i < 300; i++){
        freq = 0.5 * i / 299;
        table<<"    " << freq << "    " << x[i] << "    " << endl;
    }
    table.close();
}
int main(){
    test();
    system("pause");
    return 0;
}

C++ keshe.txt：

    0    -0.00544788    
    0.00167224    -0.00544785    
    0.00334448    -0.0054474    
    0.00501672    -0.00544542    
    0.00668896    -0.00544015    
    0.0083612    -0.00542912    
    0.0100334    -0.00540927    
    0.0117057    -0.00537699    
    0.0133779    -0.0053282    
    0.0150502    -0.00525846    
    0.0167224    -0.00516302    
    0.0183946    -0.00503697    
    0.0200669    -0.00487537    
    0.0217391    -0.0046733    
    0.0234114    -0.00442606    
    0.0250836    -0.00412926    
    0.0267559    -0.00377894    
    0.0284281    -0.0033717    
    0.0301003    -0.00290483    
    0.0317726    -0.00237641    
    0.0334448    -0.00178541    
    0.0351171    -0.00113179    
    0.0367893    -0.000416597    
    0.0384615    0.000358016    
    0.0401338    0.00118869    
    0.041806    0.00207083    
    0.0434783    0.00299862    
    0.0451505    0.003965    
    0.0468227    0.00496166    
    0.048495    0.00597915    
    0.0501672    0.00700686    
    0.0518395    0.00803317    
    0.0535117    0.00904548    
    0.0551839    0.0100304    
    0.0568562    0.0109739    
    0.0585284    0.0118612    
    0.0602007    0.0126774    
    0.0618729    0.0134074    
    0.0635452    0.0140361    
    0.0652174    0.0145484    
    0.0668896    0.0149299    
    0.0685619    0.0151668    
    0.0702341    0.0152463    
    0.0719064    0.0151565    
    0.0735786    0.014887    
    0.0752508    0.0144289    
    0.0769231    0.0137751    
    0.0785953    0.0129207    
    0.0802676    0.0118626    
    0.0819398    0.0106004    
    0.083612    0.00913603    
    0.0852843    0.00747419    
    0.0869565    0.00562229    
    0.0886288    0.00359065    
    0.090301    0.0013925    
    0.0919732    -0.000955973    
    0.0936455    -0.00343565    
    0.0953177    -0.00602447    
    0.09699    -0.00869758    
    0.0986622    -0.0114274    
    0.100334    -0.0141837    
    0.102007    -0.016934    
    0.103679    -0.0196437    
    0.105351    -0.0222762    
    0.107023    -0.0247936    
    0.108696    -0.0271564    
    0.110368    -0.0293247    
    0.11204    -0.0312581    
    0.113712    -0.0329163    
    0.115385    -0.0342594    
    0.117057    -0.035249    
    0.118729    -0.0358479    
    0.120401    -0.0360214    
    0.122074    -0.0357375    
    0.123746    -0.0349676    
    0.125418    -0.033687    
    0.12709    -0.0318756    
    0.128763    -0.0295184    
    0.130435    -0.0266061    
    0.132107    -0.0231356    
    0.133779    -0.0191106    
    0.135452    -0.0145421    
    0.137124    -0.0094486    
    0.138796    -0.00385688    
    0.140468    0.00219791    
    0.14214    0.00867184    
    0.143813    0.015512    
    0.145485    0.0226562    
    0.147157    0.030033    
    0.148829    0.0375615    
    0.150502    0.0451514    
    0.152174    0.052703    
    0.153846    0.0601073    
    0.155518    0.0672463    
    0.157191    0.073993    
    0.158863    0.0802119    
    0.160535    0.0857591    
    0.162207    0.0904827    
    0.16388    0.0942234    
    0.165552    0.0968147    
    0.167224    0.0980833    
    0.168896    0.0978498    
    0.170569    0.0959289    
    0.172241    0.0921302    
    0.173913    0.0862585    
    0.175585    0.0781141    
    0.177258    0.0674937    
    0.17893    0.0541905    
    0.180602    0.0379949    
    0.182274    0.0186946    
    0.183946    -0.00392454    
    0.185619    -0.0300787    
    0.187291    -0.0599851    
    0.188963    -0.0938624    
    0.190635    -0.13193    
    0.192308    -0.174407    
    0.19398    -0.221515    
    0.195652    -0.273474    
    0.197324    -0.330503    
    0.198997    -0.392825    
    0.200669    -0.460659    
    0.202341    -0.534225    
    0.204013    -0.613744    
    0.205686    -0.699437    
    0.207358    -0.791523    
    0.20903    -0.890224    
    0.210702    -0.995759    
    0.212375    -1.10835    
    0.214047    -1.22822    
    0.215719    -1.3556    
    0.217391    -1.4907    
    0.219064    -1.63375    
    0.220736    -1.78499    
    0.222408    -1.94464    
    0.22408    -2.11294    
    0.225753    -2.29012    
    0.227425    -2.47643    
    0.229097    -2.67211    
    0.230769    -2.87742    
    0.232441    -3.0926    
    0.234114    -3.31794    
    0.235786    -3.55369    
    0.237458    -3.80013    
    0.23913    -4.05757    
    0.240803    -4.32629    
    0.242475    -4.6066    
    0.244147    -4.89884    
    0.245819    -5.20334    
    0.247492    -5.52046    
    0.249164    -5.85056    
    0.250836    -6.19404    
    0.252508    -6.55131    
    0.254181    -6.92282    
    0.255853    -7.30902    
    0.257525    -7.71041    
    0.259197    -8.12752    
    0.26087    -8.56092    
    0.262542    -9.01121    
    0.264214    -9.47905    
    0.265886    -9.96515    
    0.267559    -10.4703    
    0.269231    -10.9953    
    0.270903    -11.541    
    0.272575    -12.1086    
    0.274247    -12.699    
    0.27592    -13.3136    
    0.277592    -13.9537    
    0.279264    -14.6208    
    0.280936    -15.3166    
    0.282609    -16.0432    
    0.284281    -16.8027    
    0.285953    -17.5976    
    0.287625    -18.431    
    0.289298    -19.3063    
    0.29097    -20.2276    
    0.292642    -21.1998    
    0.294314    -22.2287    
    0.295987    -23.3216    
    0.297659    -24.4875    
    0.299331    -25.738    
    0.301003    -27.088    
    0.302676    -28.5575    
    0.304348    -30.1744    
    0.30602    -31.9787    
    0.307692    -34.0321    
    0.309365    -36.4353    
    0.311037    -39.3733    
    0.312709    -43.2454    
    0.314381    -49.2262    
    0.316054    -66.9025    
    0.317726    -53.3326    
    0.319398    -47.1628    
    0.32107    -44.0707    
    0.322742    -42.1573    
    0.324415    -40.8826    
    0.326087    -40.0171    
    0.327759    -39.4421    
    0.329431    -39.0893    
    0.331104    -38.9161    
    0.332776    -38.8953    
    0.334448    -39.009    
    0.33612    -39.246    
    0.337793    -39.5997    
    0.339465    -40.0678    
    0.341137    -40.6514    
    0.342809    -41.3554    
    0.344482    -42.1893    
    0.346154    -43.1677    
    0.347826    -44.3132    
    0.349498    -45.6603    
    0.351171    -47.2626    
    0.352843    -49.2093    
    0.354515    -51.6612    
    0.356187    -54.9552    
    0.35786    -60.0097    
    0.359532    -71.935    
    0.361204    -67.0535    
    0.362876    -59.2737    
    0.364548    -55.531    
    0.366221    -53.1603    
    0.367893    -51.5022    
    0.369565    -50.29    
    0.371237    -49.3892    
    0.37291    -48.723    
    0.374582    -48.2439    
    0.376254    -47.9204    
    0.377926    -47.7317    
    0.379599    -47.6631    
    0.381271    -47.7049    
    0.382943    -47.851    
    0.384615    -48.0978    
    0.386288    -48.4445    
    0.38796    -48.8926    
    0.389632    -49.4463    
    0.391304    -50.1124    
    0.392977    -50.9019    
    0.394649    -51.8306    
    0.396321    -52.9216    
    0.397993    -54.2095    
    0.399666    -55.7476    
    0.401338    -57.6231    
    0.40301    -59.9927    
    0.404682    -63.1809    
    0.406355    -68.0578    
    0.408027    -79.1678    
    0.409699    -75.8997    
    0.411371    -67.671    
    0.413043    -63.7752    
    0.414716    -61.3013    
    0.416388    -59.5566    
    0.41806    -58.2645    
    0.419732    -57.2867    
    0.421405    -56.5441    
    0.423077    -55.9875    
    0.424749    -55.5844    
    0.426421    -55.3127    
    0.428094    -55.1567    
    0.429766    -55.1054    
    0.431438    -55.1508    
    0.43311    -55.2877    
    0.434783    -55.5127    
    0.436455    -55.8244    
    0.438127    -56.2227    
    0.439799    -56.7093    
    0.441472    -57.2878    
    0.443144    -57.9636    
    0.444816    -58.7449    
    0.446488    -59.6431    
    0.448161    -60.6745    
    0.449833    -61.8623    
    0.451505    -63.2405    
    0.453177    -64.8613    
    0.454849    -66.8094    
    0.456522    -69.2364    
    0.458194    -72.4524    
    0.459866    -77.2744    
    0.461538    -87.6981    
    0.463211    -86.3822    
    0.464883    -77.7015    
    0.466555    -73.7424    
    0.468227    -71.2591    
    0.4699    -69.5153    
    0.471572    -68.221    
    0.473244    -67.2308    
    0.474916    -66.4609    
    0.476589    -65.8581    
    0.478261    -65.3861    
    0.479933    -65.0186    
    0.481605    -64.7354    
    0.483278    -64.5208    
    0.48495    -64.3617    
    0.486622    -64.2473    
    0.488294    -64.1682    
    0.489967    -64.1162    
    0.491639    -64.0844    
    0.493311    -64.0668    
    0.494983    -64.0584    
    0.496656    -64.0552    
    0.498328    -64.0545    
    0.5    -64.0545    

将keshe.txt里的数据用matlab画图：

MATLAB实现代码：

a=data(:,1);
b=data(:,2);
figure
plot(a,b);
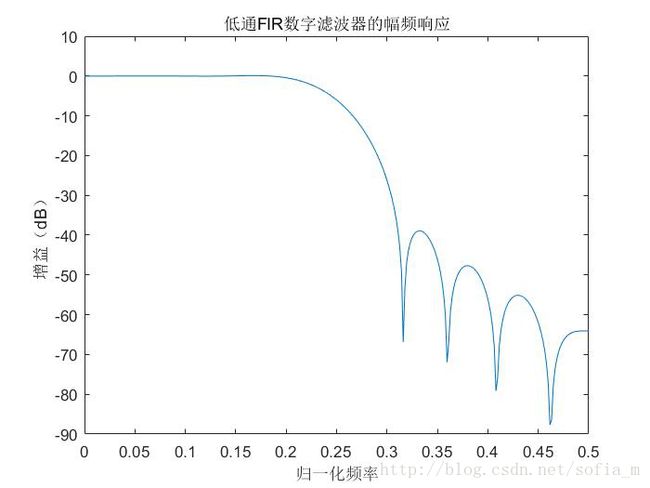
xlabel('归一化频率');
ylabel('增益(dB)');
title('低通FIR数字滤波器的幅频响应')

实验结果图像：

---

四、参考文献

杨路明. C语言程序设计教程.北京邮电大学出版社.2005

高西全 丁玉美.数字信号处理.西安电子科技大学出版社. 2008.8

殷福亮 宋爱军.数字信号处理C语言程序集.辽宁科学技术出版社.1997.7