Spark大数据分析-GraphX：基础

顶点对象与边对象

弹性分布式数据集（RDD）是构建Spark程序的基础模块，它提供了灵活、高效、并行化数据处理和容错等特性。在GraphX中，图的基础类为Graph，它包含两个RDD：一个为边RDD，另一个为顶点RDD。

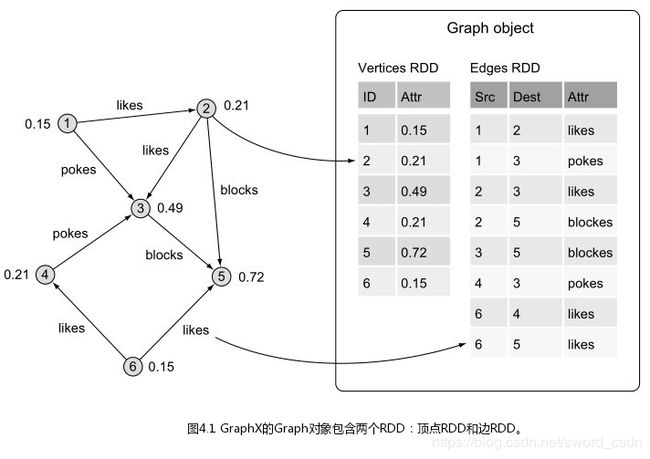
与其他图处理系统和图数据库相比，基于图概念和图处理原语的GraphX，它的一大优势在于，既可以将底层数据看作一个完整的图，使用图概念和图处理原语；也可以将它们看作独立的边RDD和顶点RDD，使用数据并行处理原语，进行mapped、joined、transformed等操作。

在GraphX里，没必要（从某些特定顶点开始）“遍历”全图以得到想要的边和顶点。例如，对顶点属性数据进行转换可以一下子完成，而在其他图处理系统和图数据库里，类似的操作就没那么方便了，需要两步：先执行必要的查询，然后再对查询的结果顶点集执行转换操作。

可以用给定的边RDD和顶点RDD构建一个图。一旦构建好图，就可以用函数edges()和vertices()来访问边和顶点的集合。

import org.apache.spark.graphx._

val myVertices = sc.makeRDD(Array((1L, "Ann"), (2L, "Bill"),
 (3L, "Charles"), (4L, "Diane"), (5L, "Went to gym this morning")))

val myEdges = sc.makeRDD(Array(Edge(1L, 2L, "is-friends-with"),
 Edge(2L, 3L, "is-friends-with"), Edge(3L, 4L, "is-friends-with"),
 Edge(4L, 5L, "Likes-status"), Edge(3L, 5L, "Wrote-status")))

val myGraph = Graph(myVertices, myEdges)
myGraph.vertices.collect
myGraph.edges.collect

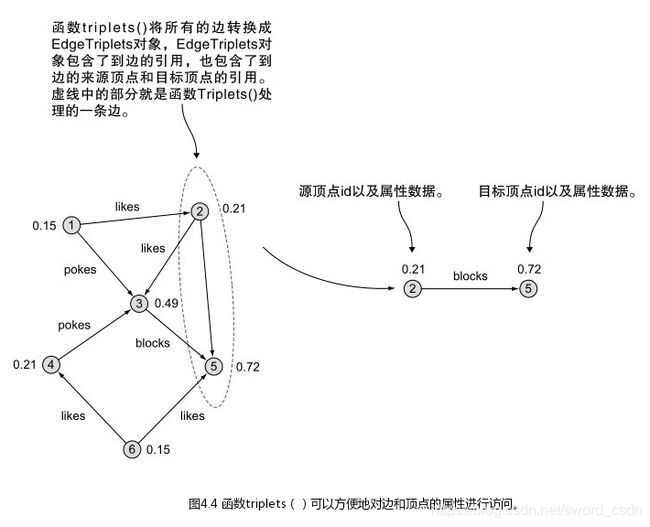
可以使用triplets()方法，根据VertexId将顶点和边联合在一起。Graph本来是将数据分开存储在对应的边RDD和顶点RDD内，triplets()函数只不过是方便地将它们联合在一起。

myGraph.triplets.collect

函数triplets()返回EdgeTriplet[VD,ED]类型的RDD，它是Edge[ED]的子类，并包含边的源顶点和目标顶点的引用。
EdgeTriplet的常用成员属性

字段	描述
Attr	边的属性数据
srcId	边的源顶点的ID
srcAttr	边的源顶点的属性数据
dstId	边的目标顶点的Id
dstAttr	边的属性数据

EdgeTriplet类提供了访问边（以及边属性数据）以及源顶点和目标顶点属性数据的方法。GraphX可以便捷地访问边和顶点数据，让图处理任务更简单易用。

mapping操作

GraphX Map/Reduce操作中最有价值的函数是aggregateMessages()（代替已被废弃的mapReduceTriplets函数）。在实际使用这个函数前，首先让我们来看看更简单的mapTriplets()函数，这也会引出GraphX的另一个重要概念。本书中涉及的很多转换操作都会从原来的图生成一个新图。虽然我们也可以自己对边和顶点转换来创建一个新图，这两者的最终结果或许是一致的，但这样就不能利用GraphX提供的底层优化功能了。

简单的图转换

在边属性上增加布尔类型的属性来表示一个条件限制，1、属性中包含“is-friends-with”的边；2、边所关系的源顶点属性中包含a的。
在边属性上增加布尔类型的属性来表示一个条件限制

myGraph.mapTriplets(t => (t.attr, t.attr=="is-friends-with" &&
 t.srcAttr.toLowerCase.contains("a"))).triplets.collect

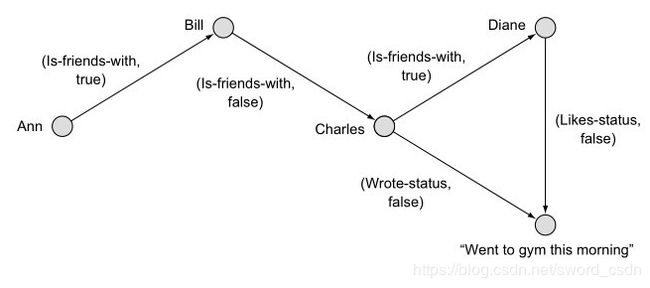
尽管mapTriplets()有两个可选参数，但这里我们只用了第一个参数。这个参数是一个匿名函数，它传入一个EdgeTriplet对象作为输入参数，返回一个包含二元组（String,Boolean）的Edge类型。与允许转变Edge类的mapTriplets()类似，函数mapVertices()允许我们直接转变Vertex类。

Map/Reduce

很多图处理任务需要聚集从周围本地邻居顶点发出的消息。这里的邻居指的是顶点周围直接相关联的边和顶点。
统计每个顶点的“出度”——即对于每个顶点而言，离开该顶点的边的条数。

myGraph.aggregateMessages[Int](_.sendToSrc(1), _ + _).collect

这里仅仅需要aggregateMessages函数就可以完成任务

def aggregateMessage[Msg](sendMsg:EdgeContext[VD,ED,Msg]=>Unit,
	mergeMsg:(Msg,Msg)=>Msg
):VertexRDD[Msg]

aggregateMessages的两个参数是sendMsg和mergeMsg，它们提供了转换和聚合的能力。

sendMsg

sendMsg函数以EdgeContext作为输入参数，没有返回值。EdgeContext接口的实现类提供了两个Msg的sendMsg函数。

sendToSrc：将Msg类型的消息发送给源顶点。
sendToDst：将Msg类型的消息发送给目标顶点。

sendToSrc是针对源顶点的统计，而sendToDst则是针对目标顶点的统计。在sendMsg方法内部，参数EdgeContext用于检查边、源顶点、目标顶点三者的属性值。在这个例子中，因为需要计算每个顶点发出的边数，每次累加的值为1，所以传入的消息是1。（可以感性理解成，这个1是沿着边给到顶点的，一个顶点有多少个边，就有多少1）

mergeMsg

每个顶点收到的所有消息都会被聚集起来传递给mergeMsg函数。这个函数定义了如何将顶点收到的所有消息转换成我们需要的结果。在示例代码中，我们将所有发给源顶点的数字1累加起来得出边的总数。这就是匿名函数" _ "使用+操作完成的。

在每个顶点上应用mergeMsg函数最终会返回一个VertexRDD[Int]对象。VertexRDD是一个包含了二元组的RDD，包括了顶点的ID以及该顶点的mergeMsg操作的结果。需要注意的一点是，由于顶点#5不含有任何出边，它接收不到任何消息，所以它不会出现在结果VertexRDD中。

RDD的join()操作用于匹配VertexId与顶点数据

myGraph.aggregateMessages[Int](_.sendToSrc(1),
 _ + _).join(myGraph.vertices).collect

上面的做法看起来还是有点烦琐。因为其实后面用不到这些VertexId，所以可以使用RDD的map()函数去掉它们，可以使用二元组的swap()方法交换两个元素的顺序，将可读的顶点名放在出度值之前使得输出更为美观。

myGraph.aggregateMessages[Int](_.sendToSrc(1),
 _ + _).join(myGraph.vertices).map(_._2.swap).collect

迭代的Map/Reduce

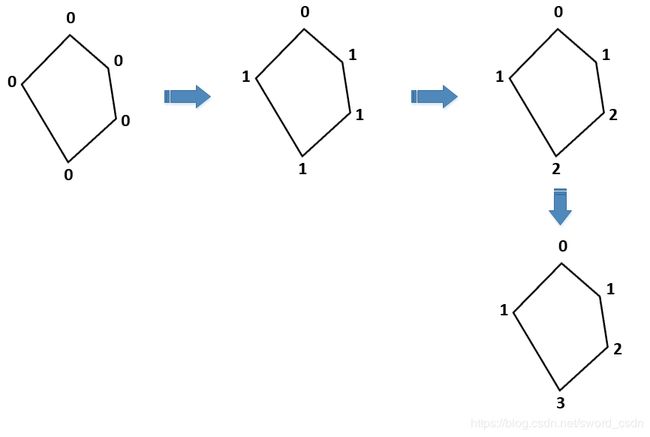
大多数的算法都包含多次迭代。aggregateMessages可用于这类算法，其仅需要基于邻边和顶点发送过来的消息进而不断更新每个顶点的状态。例如：为每个顶点标记上离它最远的根顶点的距离。

首先我们对aggregateMessages会调用到的sendMsg和mergeMsg进行定义。在这里不把sendMsg和mergeMsg作为匿名函数传给aggregateMessages函数，而是显式地定义sendMsg和mergeMsg函数。

在函数式编程中实现迭代通常采用递归的方式，所以接下来定义一个用于递归的辅助函数propagateEdgeCount，它会持续调用aggregateMessages。

//这个方法会在没条边上调用
def sendMsg(ec: EdgeContext[Int,String,Int]): Unit = {
  ec.sendToDst(ec.srcAttr+1)
}

def mergeMsg(a: Int, b: Int): Int = {
  math.max(a,b)
}

def propagateEdgeCount(g:Graph[Int,String]):Graph[Int,String] = {    
  val verts = g.aggregateMessages[Int](sendMsg, mergeMsg)
  val g2 = Graph(verts, g.edges)
  val check = g2.vertices.join(g.vertices).
       map(x => x._2._1-x._2._2).
       reduce(_ + _)
  if (check > 0)
    propagateEdgeCount(g2)
  else
    g
}

//创建边信息
val myEdges = sc.parallelize(Array(
  Edge(1L, 2L, "friends"),
  Edge(2L, 3L, "friends"),
  Edge(3L, 4L, "colleagues"),
  Edge(3L, 5L, "friends"),
  Edge(4L, 5L, "colleagues")
))
val myGraph = Graph(myVertices, myEdges)
//设置顶点属性, 将所有顶点的属性初始化为 0
val initGraph = myGraph.mapVertices((_,_) => 0)
propagateEdgeCount(initGraph).vertices.collect.foreach(println(_))

整个递归过程示例图如下所示：

生成图

可使用GraphGenerators对象来生成一些随机图。当需要快速验证一些图函数或图算法时，这种方法十分有效。其中，generateRandomEdges（）是生成图函数的一个辅助函数；单独使用它并不是那么有效，因为它会接收一个单一的顶点ID作为参数输入，而接下来所有生成的边都会跟这个顶点有关。

确定的图

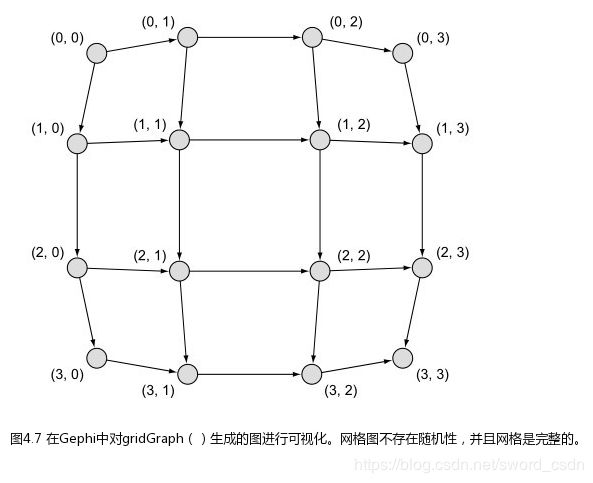
网格图

网格图的顶点和边符合特定的模式，就像是在一个二维的网格或矩阵中。每一个顶点都用它在网格中行和列的位置作为标签（例如，左上顶点的标签为（0,0））。每个顶点都和它上、下、左、右的直接邻居相连。

val pw = new java.io.PrintWriter("gridGraph.gexf")
pw.write(toGexf(util.GraphGenerators.gridGraph(sc, 4, 4)))
pw.close

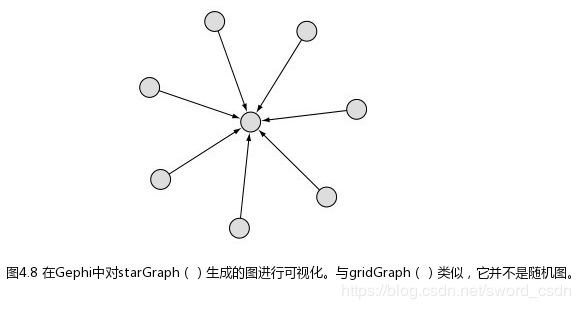
星形图

星形图指的是有一个顶点通过边与所有其他顶点相连，除此之外图中不存在其他边。

val pw = new java.io.PrintWriter("starGraph.gexf")
pw.write(toGexf(util.GraphGenerators.starGraph(sc, 8)))
pw.close

随机图

GraphX提供了两种随机生成图的方法：一个是单步算法（称为对数正态算法），它将特定数量的边与各个顶点关联起来；另一个是多步算法（称为R-Mat算法），它会生成与现实世界比较相近的图。

对数正态图

对数正态图（log normal graph）关注的是生成图的每个顶点的出度值分布。它保证在对所有的出度值绘制直方图时，你可以看到一个对数正态分布的形状（高斯钟形曲线），这意味着log（d）服从正态分布（d代表顶点的度值）。

val logNormalGraph = util.GraphGenerators.logNormalGraph(sc, 15)
val pw = new java.io.PrintWriter("logNormalGraph.gexf")
pw.write(toGexf(logNormalGraph))
pw.close
logNormalGraph.aggregateMessages[Int](
    _.sendToSrc(1), _ + _).map(_._2).collect.sorted

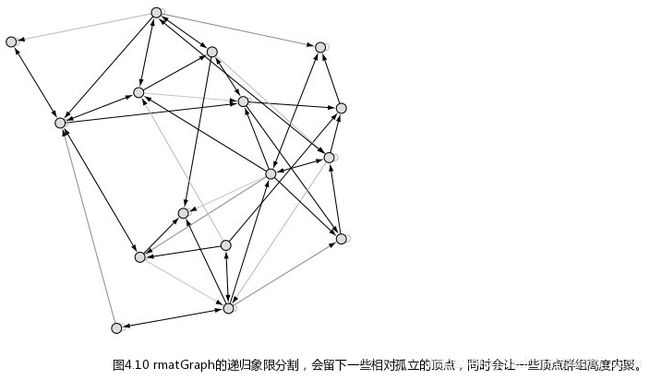
基于程序化流程的：R-MAT图

R-MAT，代表递归矩阵，用于模拟典型的社交网络架构。与之前的基于度值的logNormalGraph（）函数相反，rmatGraph（）进行“程序化”的过程。

val pw = new java.io.PrintWriter("rmatGraph.gexf")
pw.write(toGexf(util.GraphGenerators.rmatGraph(sc, 32, 60)))
pw.close