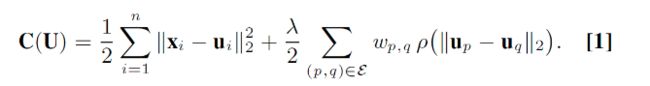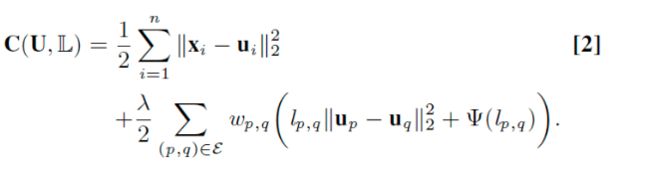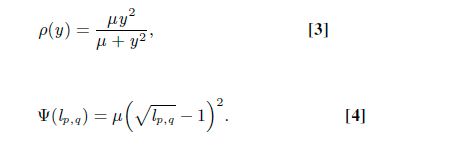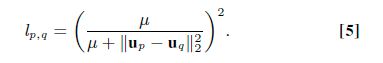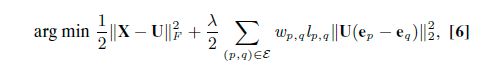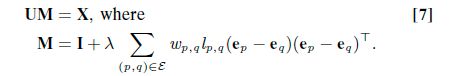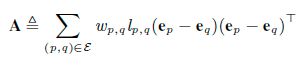Robust continuous clustering

【Abstract】

聚类是科学数据分析的基本步骤。它被广泛应用于科学领域。尽管经过了几十年的研究，现有的聚类算法在高维方面的有效性有限，并且常常需要针对不同的域和数据集调整参数。提出了一种跨领域的聚类算法，该算法具有较高的精度，可有效地扩展到高维、大数据集。该算法以鲁棒统计为基础，优化了平滑连续的目标，并解决了大量混合的聚类问题。目标的连续性也允许集群作为模块集成到端到端的特性学习管道中。我们通过扩展算法来实现联合聚类和通过有效地优化一个连续的全局目标来降低维数来证明这一点。所提出的方法是通过大数据集来评估的，这些数据集包括人脸、手写数字、物体、新闻专线文章、来自航天飞机的传感器读数和蛋白质表达水平。我们的方法在所有数据集上都达到了很高的精度，平均排名比最好的先验算法高出3倍。

【Introduction】

我们提出了一种快速、简便、高效的高维聚类算法。该算法使用标准的数值方法来优化一个清晰的连续目标。不需要预先知道集群的数量。

 

我们的公式是基于最近的凸松弛聚类(25,26)。然而，我们的目标是故意不凸出。我们使用降阶的鲁棒估计器，通过优化单个连续目标，即使是高度混合的集群也可以被解开。尽管目标具有非凸性，但仍然可以使用标准的线性最小二乘解算器进行优化，该解算器具有很高的效率和可伸缩性。由于该算法将聚类表示为基于鲁棒估计的连续目标优化，因此我们将其称为鲁棒连续聚类(RCC)。

 

该方法的一个特点是将聚类问题简化为连续目标的优化问题。这支持在端到端特性学习管道中集成集群。我们通过扩展RCC来执行联合聚类和降维来证明这一点。这种扩展的算法称为RCC-DR，它学习将数据嵌入到一个低维空间中，并将数据聚集在这个低维空间中。嵌入和聚类是通过优化一个明确的全局目标的算法来共同完成的。

 

【正文】

RCC是一种聚类方法，聚类的数量不用事先预知，通过优化下面的式子来实现聚类：

 

X=[x1,x2,...,xn]是输入的数据，U=[u1,u2,...,un]是这些点集的表示，对U进行优化，得到聚类的结果。ε是一个图的边所组成的集合，这个图是由m-kNN方法生成的。权重wp,q平衡每一个数据点成对的贡献，λ平衡不同项之间的权重。ρ是一个正则项，它用来起到惩罚作用。上式中，第二项与均值漂移目标(9)相关。RCC目标的不同之处在于，它包含一个额外的数据项，使用一个稀疏(而不是完全连接)连接结构，并基于稳健估计。

为了便于优化，作者在随后构建了一个目标函数，并且证明了他们之间等价，

 

给每个连接（p,q）引入了一个辅助变量lp.q。L={lp,q}，作者联合优化U和L。

Ψ（lp,q）是当忽略连接（p,q）时产生的惩罚。当有连接时，Ψ（lp,q）->1;当没有连接时，（lp,q）->0.

 

各种各样的鲁棒估计量ρ（.)都有相应的罚函数Ψ(.），可以使式子（1）和（2)等价，就是说优化(1)或者(2)最后得到的U都是一样的。因为优化式子(2)方便，作者优化式子(2)。

当（1）采用Geman–McClure估计量ρ（.) 和 （2) 采用以下的Ψ(.）惩罚函数时，式子（1）和（2)等价。

目标2对于（U，L）都是凸函数，优化时采用先固定一个变量，优化另一个变量的方法，两个变量轮流交替优化。

 

当U固定时，没有个lp,q的最优值为：

当L固定时，优化问题变成：

ei是一个向量指示器，表明U的第i个元素是1。

 

上面是一个最小线性二乘问题。

 

I是一个n*n的方阵，我们可以得到

式子（7)中的每一行U可以独立并行求解。根据式子(7)，我们可以将lambda设置为

在RCC算法前，作者先用mutual-kNN算法获取连接每个点的图，然后根据该图执行RCC算法。这两种算法总结如下：