Matlab2019b关于窗函数的详细设置(dsp.window)
使用窗函数来截取一段无限长(非常长:远大于一帧的长度)的信号,形象的来描述就是透过一个窗户来看一个信号,这个窗户的形状会对信号有一定的影响。
看大佬的解释看不懂,水平不足,下面是从自身使用的感觉来讲的,如果不对还请指点包容,感激不尽。
使用窗函数可以减少截断时的噪声(一刀切边缘会产生很多的高频谐波(吉布斯效应),从而造成频谱泄露(FFT的时候会搞出来很多原本信号没有的频率),所以切下去的时候要温柔一点,搞一点弧线,又不能太影响信号本身,继而出现了下面N种窗函数)
网上程序多为使用window函数构建,本人使用dsp.window构建,处理速度更快,程序更为精简。
%% 窗函数
clc;
Fs = 1000; % Sampling frequency
T = 1/Fs; % Sampling period
L = 1500; % Length of signal
t = (0:L-1)*T; % Time vector
X = 0.7*sin(2*pi*50*t)+ 0.9*cos(2*pi*90*t)+rand(4,1500);%如果要看到窗函数的作用,数据在每个通道内必须有大于两帧的长度
win = dsp.Window
win.WindowFunction='Hamming';
win.WeightsOutputPort=true;
win.StopbandAttenuation=50;%仅当Chebyshev型窗函数时有效,数值越大,带宽越窄
win.Beta=10;%仅当Kaiser型窗函数时有效
win.NumConstantSidelobes=4;%仅当Taylor型窗函数时有效
win.MaximumSidelobeLevel=-30;%仅当Taylor型窗函数时有效
win.Sampling='Symmetric';%仅当Blackman;Hamming;Hann;Hanning型窗函数时有效
%用法
[Y,W] = win(X);
wvtool(W)%可以查看窗函数的工具
subplot(2,1,1)
plot(t,X)
subplot(2,1,2)
plot(t,Y)
常见窗函数
矩形窗
通常如果不加窗函数,就是默认为矩形窗。
ω ( n ) = 1 \displaystyle \omega (n)=1 ω(n)=1
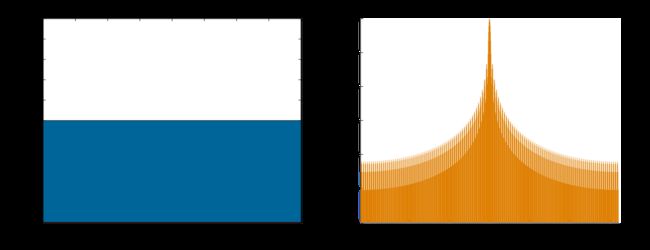
高斯窗
ω ( n ) = e − 1 2 ( n − ( N − 1 ) / 2 σ ( N − 1 ) / 2 ) 2 σ ≤ 0.5 \displaystyle \begin{array}{l}\omega (n)={{e}^{{-\frac{1}{2}{{{(\frac{{n-(N-1)/2}} {{\sigma (N-1)/2}})}}^{2}}}}}\\\sigma \le 0.5\end{array} ω(n)=e−21(σ(N−1)/2n−(N−1)/2)2σ≤0.5

汉明窗
ω ( n ) = a 0 − ( 1 − a 0 ) ⋅ cos ( 2 π n N − 1 ) , 0 ≤ n ≤ N − 1 , a 0 = 0.53836 H a m m i n g , a 0 = 0.5 H a n n \displaystyle \begin{array}{l}\omega (n)={{a}_{0}}-(1-{{a}_{0}})\cdot \cos (\frac{{2\pi n}}{{N-1}}),0\le n\le N-1,\\{{a}_{0}}=0.53836Hamming,{{a}_{0}}=0.5Hann\end{array} ω(n)=a0−(1−a0)⋅cos(N−12πn),0≤n≤N−1,a0=0.53836Hamming,a0=0.5Hann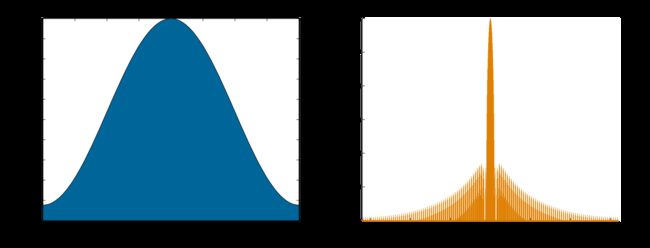
汉宁窗
巴特雷特窗
ω ( n ) = 2 N − 1 ⋅ ( N − 1 2 − ∣ n − N − 1 2 ∣ ) \displaystyle \omega (n)=\frac{2}{{N-1}}\cdot (\frac{{N-1}}{2}-|n-\frac{{N-1}}{2}|) ω(n)=N−12⋅(2N−1−∣n−2N−1∣)
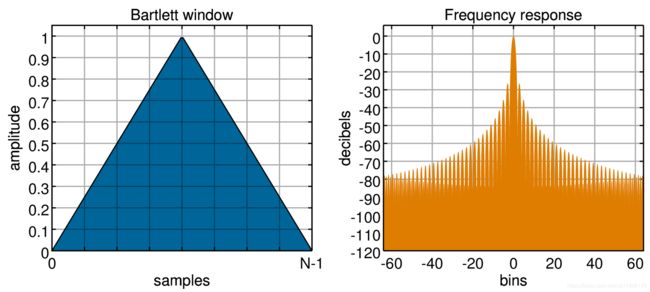
三角窗
ω ( n ) = 2 N ⋅ ( N 2 − ∣ n − N − 1 2 ∣ ) \displaystyle \omega (n)=\frac{2}{N}\cdot (\frac{N}{2}-|n-\frac{{N-1}}{2}|) ω(n)=N2⋅(2N−∣n−2N−1∣)
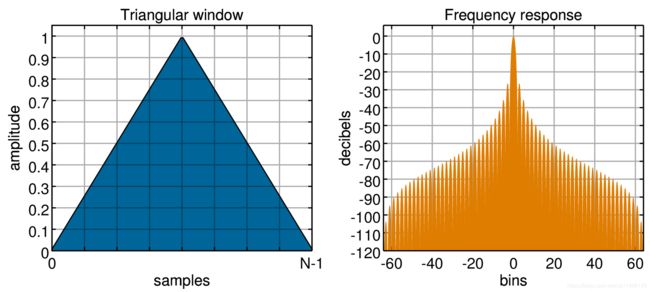
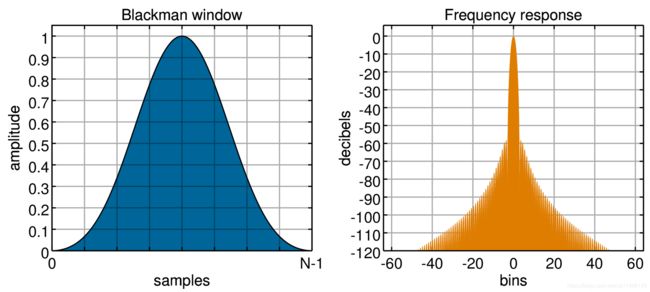
布拉克曼窗
ω ( n ) = a 0 − a 1 cos ( 2 π n N − 1 ) + a 2 cos ( 4 π n N − 1 ) , a 0 = 0.42 , a 1 = 0.5 , a 2 = 0.08 \displaystyle \omega (n)={{a}_{0}}-{{a}_{1}}\cos (\frac{{2\pi n}}{{N-1}})+{{a}_{2}}\cos (\frac{{4\pi n}}{{N-1}}),{{a}_{0}}=0.42,{{a}_{1}}=0.5,{{a}_{2}}=0.08 ω(n)=a0−a1cos(N−12πn)+a2cos(N−14πn),a0=0.42,a1=0.5,a2=0.08
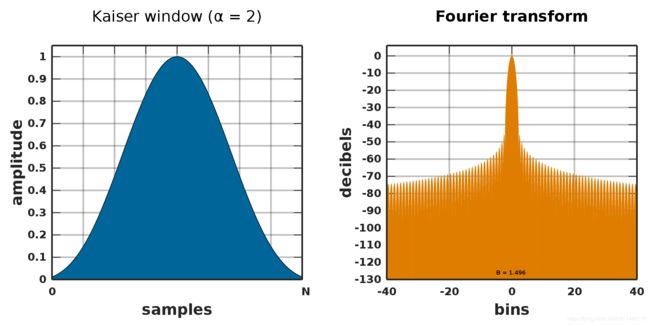
凯瑟窗
ω ( n ) = I 0 ( π a 1 − ( 2 n N − 1 − 1 ) 2 ) I 0 ( π a ) \displaystyle \omega (n)=\frac{{{{I}_{0}}(\pi a\sqrt{{1-{{{(\frac{{2n}}{{N-1}}-1)}}^{2}}}})}}{{{{I}_{0}}(\pi a)}} ω(n)=I0(πa)I0(πa1−(N−12n−1)2)
参考资料
Copyright © 2020 by RichardYang. All rights reserved.
仅供参考,严禁转载,感谢。