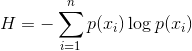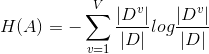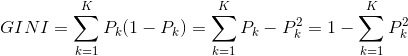决策树——ID3/C4.5/CART算法

最近在梳理一些算法资料，正好趁这个机会将一些积累写在博客上，方便以后回顾和完善。

---

目录

 

1，决策树的基本概念

2，决策时的构建

3，ID3算法

4，C4.5算法

5， CART树

6，剪枝

7，决策树的优缺点

---

1，决策树的基本概念

---

决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，如图1所示，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度，算法ID3、C4.5和C5.0生成决策树使用的是信息学理论中熵的概念。

图1，决策树

决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。

 

相关关键词：

（1）根结点(Root Node)：它表示整个样本集合，并且该节点可以进一步划分成两个或多个子集。

（2）拆分(Splitting)：表示将一个结点拆分成多个子集的过程。

（3）决策结点(Decision Node)：当一个子结点进一步被拆分成多个子节点时，这个子节点就叫做决策结点。

（4）叶子结点(Leaf/Terminal Node)：无法再拆分的结点被称为叶子结点。

（5）剪枝(Pruning)：移除决策树中子结点的过程就叫做剪枝，跟拆分过程相反。

（6）分支/子树(Branch/Sub-Tree)：一棵决策树的一部分就叫做分支或子树。

（7）父结点和子结点(Paren and Child Node)：一个结点被拆分成多个子节点，这个结点就叫做父节点；其拆分后的子结点也叫做子结点。

2，决策时的构建

---

决策树的构造过程一般分为3个部分，分别是特征选择、决策树生产和决策树裁剪。

（1）特征选择：

特征选择表示从众多的特征中选择一个特征作为当前节点分裂的标准，如何选择特征有不同的量化评估方法，从而衍生出不同的决策树，如ID3（通过信息增益选择特征）、C4.5（通过信息增益比选择特征）、CART（通过Gini指数选择特征）等。

目的（准则）：使用某特征对数据集划分之后，各数据子集的纯度要比划分钱的数据集D的纯度高（也就是不确定性要比划分前数据集D的不确定性低）

（2）决策树的生成

根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。这个过程实际上就是使用满足划分准则的特征不断的将数据集划分成纯度更高，不确定行更小的子集的过程。对于当前数据集的每一次划分，都希望根据某个特征划分之后的各个子集的纯度更高，不确定性更小。

（3）决策树的裁剪

决策树容易过拟合，一般需要剪枝来缩小树结构规模、缓解过拟合。

决策树家族有很多算法，不同的决策树算法主要体现在特征选择方法上，为人熟知和比较常用的有ID3、C4.5、CART等，他们有相同点，也有不同点，下面分别介绍。

3，ID3算法

---

ID3算法在构造决策树各个节点及选择特征时候的准则是信息增益。关于信息、熵、交叉熵的概念请参考这里。

所谓信息增益Gain，就是分类前的信息墒减去分类后的信息熵，其意义就是衡量节点分裂后系统的混乱度（信息熵）的变化。很显然这里要选择信息增益最大的特征，数据集合D的混乱度最大化减少。

信息熵是信息论中的概念，是信息量的期望，信息量表示为：

                                                                    

那么信息熵为H：

                                                          

在得知一个特征信息A后，信息熵会减少为，那么信息增益表示为：

                                                      

                                                                       

看公式可能还不够直观，所以举个经典的例子：

苹果编号	红不红	圆不圆	甜不甜
1	1	1	yes
2	1	1	yes
3	1	0	no
4	0	1	no
5	0	1	no

简要说明计算过程：先计算此状态下的信息熵

H1=-(2/5)log(2/5)-(3/5)log(3/5)

如果按照红不红分，计算分离后的信息熵：

H2= -1/3log(1/3)-(2/3)log(2/3)+1log(1)

增益G = H1 – H2

4，C4.5算法

---

ID3采用信息增益有个缺点，一般会选择属性多的特征（属性多分的细，信息明确，增益大）。所以C4.5算法在此基础上做了改进，C4.5算法与ID3算法很相似，在生成决策树过程中采用信息增益比来选择特征。

                                               

                                                

当A特征属性越多多时信息熵就越大，对于Gain(D,A)的惩罚就越大，因而在选择特征时避免了属性多的特征带来的影响，当然这样会导致容易选取属性值少的，一般的解决方法是先把信息增益低于平均水平的去掉，再选择。

5， CART树

---

CART树与ID3和C4.5有比较大的不同，首先它是二叉树，简化了决策树的生成规模，提高了生成效率；其次CART树采用GINI系数作为节点分裂的特征选择标准，因为不涉及对数计算，所以其计算速度比较快；而且，它可以处理分类和回归问题。

                                                        

CART树的特点：

1）节点分裂标准：基尼系数。

2）处理数据：离散、连续（排序，分别计算每个点的二分类GINI系数，选择最小的点）

3）节点分支：二叉树，每次节点分成两份分别进入左子树和右子树。

4）可以做回归：取节点均值作为预测值，均方差作为分裂标准；也可以做分类：叶子节点处投票预测，基尼系数为分裂标准

5）二叉树，简化模型，GINI系数减少计算。

6，剪枝

---

预剪枝：节点分裂时，计算分裂前后的识别率变化，如果没有提高，即使有信息变化，也不再分裂。容易欠拟合。

后剪枝：决策树建立完成之后，判断删除子节点后的识别率变化，如果能够提高就剪掉，降低过拟合风险。

后剪枝要优于预剪枝。

7，决策树的优缺点

---

优点：

简单、直观，可解释性强。

缺点：

·贪婪算法，容易过拟合，所以一般需要剪枝。

·容易陷入局部最优，过分依赖于某个独立特征。

·不稳定，受数据的影响较大，即方差大，也就是过拟合。

·属性值较多的特征影响较大，在讲C4.5算法的时候提到过。

为了应对这些问题，在决策树的基础上产生了两种算法：RF与GBDT/XGBoost，两种算法都是集成学习算法，需要建立多棵决策树，但是两者分别从优化偏差与方差的角度来建立模型的。