【机器学习】【EM算法-1】数学基础:正/负定矩阵+凹(凸)函数+(最大)似然函数+Hessian矩阵+Jensen不等式。

EM算法

EM（Expectation Maximization Algorithm），期望最大值算法推理时，用到了这些数学知识：

（1）正/负定矩阵

（2）[严格]凹函数

（3）[严格]凸函数

（4）[最大]似然函数

（5）Hessian矩阵

（6）Jensen不等式

1.正/负定矩阵

positive definite matrix，正定矩阵;

negative definite matrix，负定矩阵

正定矩阵性质：

（1）A是一个正定矩阵，则|A|行列式 > 0，即正定矩阵的行列式恒为正

（2）正定矩阵A的逆矩阵也是正定矩阵

（3）如果A，B是正定矩阵，则A+B也是正定矩阵

（4）正实数与正定矩阵的乘积是正定矩阵

（5）实对称矩阵A正定 当且仅当 A与单位矩阵合同

          

2.正定矩阵的充要条件

3.怎么判别对称矩阵A的正定型？？？

根据正定矩阵的定义及性质，判别对称矩阵A的正定性有两种方法：

（1）求出A的所有特征值。

         正定：若A的特征值均为正数，则A是正定的；

         负定：若A的特征值均为负数，则A为负定的。

（2）计算A的各阶主子式。

         正定：若A的各阶主子式均大于零，则A是正定的；

         负定：若A的各阶主子式中，奇数阶主子式为负，偶数阶为正，则A为负定的。

4.[严格]凹/凸函数

如果函数f(x)满足如下条件，则f(x)是凹函数：

上式子中如果去掉＝，只有＜，则f(x)就是严格凹函数。

如果函数f(x)满足如下条件，则f(x)是凸函数：

上式子中如果去掉=，只有>，则f(x)就是严格凸函数

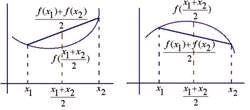
比如下面函数，就是一个凹函数：

二阶导判断凹函数还是严格凹函数：

如果f(x的二阶导数在区间上>=0，则f(x)为凹函数

如果f(x)的二阶导数在区间上>0成立，则f(x)为严格凹函数，

如下图所示左边的图形是严格凹函数，右边的是严格凸函数：

5.[最大]似然函数

统计学中，似然函数是一种关于统计模型参数的函数。

给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ点后变量x的概率：L(θ|x) = P(X=x|θ)

可知：似然函数是一种条件概率函数

下面的一个示例是来自其他文章的一部分：

考虑投掷一枚硬币的实验。通常来说，已知投出的硬币正面朝上和反面朝上的概率各自是p_H = 0.5，便可以知道投掷若干次后出现各种结果的可能性。比如说，投两次都是正面朝上的概率是0.25。用条件概率表示，就是：

其中H表示正面朝上。

在统计学中，我们关心的是在已知一系列投掷的结果时，关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型：假设硬币投出时会有p_H 的概率正面朝上，而有1 − p_H 的概率反面朝上。这时，条件概率可以改写成似然函数：

也就是说，对于取定的似然函数，在观测到两次投掷都是正面朝上时，p_H = 0.5 的似然性是0.25（这并不表示当观测到两次正面朝上时p_H = 0.5 的概率是0.25）。

如果考虑p_H = 0.6，那么似然函数的值也会改变。

注意到似然函数的值变大了。这说明，如果参数p_H 的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设p_H = 0.5时更大。也就是说，参数p_H 取成0.6 要比取成0.5 更有说服力，更为“合理”。总之，似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。

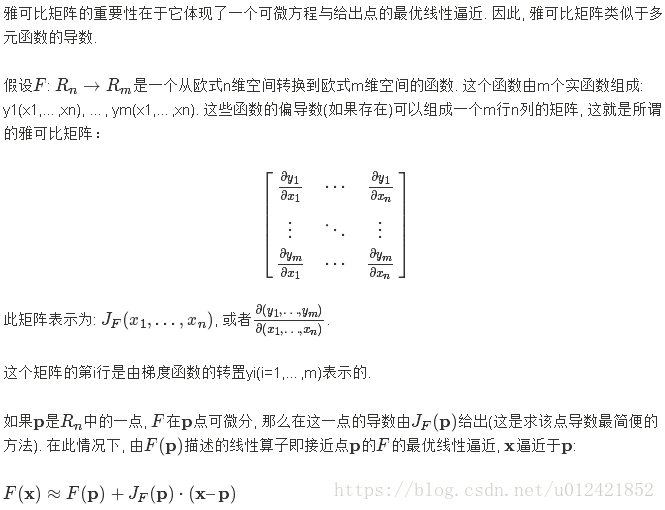
6.Hessian矩阵

7.Jensen不等式

参考文献：

[1]https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/11030459?fr=aladdin

[2]http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/

(end)