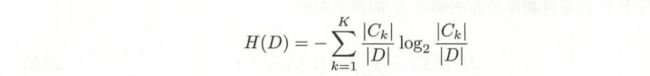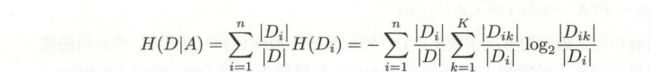SAM--Chap 5 决策树自我梳理

• 树形结构，if-then规则

• 3个步骤： 特征选择 决策树的生成 决策树的修剪
  决策树的生成对应于模型的局部选择，决策树的剪枝对应于模型的全局选择
  决策树的生成只考虑局部最优，相对地，决策树的剪枝考虑全局最优

• 常用算法: ID3 C4.5 CART

1. 特征选择

通常特征选择的准则是 信息增益或信息增益比 （information gain）
特征选择是决定用哪个特征来划分特征空间

Entropy

随机变量X的熵定义为：

熵越大 随机变量的不确定就越大。which is obvious 你发生这件事的概率越小 那你发生时从中得到信息的价值就越会越大

对数以2为底，称bit，以e为底，称nat。熵只依赖于X的分布，与取值无关，所以也可以记作H（p）

条件熵 H(Y|X) conditional entropy：

Information gain 表示得知特征X的信息而使得类Y的信息的不确定性减少的程度

这个差值也成为 mutual information. 信息增益大的特征具有更强的分类能力

信息增益算法步骤：

• 输入：训练集D和特征A；

• 输出： g(D,A)
  计算 D的经验熵 H(D) ->
  

  计算特征A对D的经验条件熵 H (D|A) ->
  

  计算信息增益 g(D,A) = H (D) - H(D|A)
  

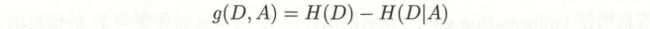
  最后根据哪个特征得到的最大 选取那个特征， 也可以用information gain ratio作为准则

2. 决策树的生成

ID3

The central focus of the ID3 algorithm is selecting which attribute to test at each node in the tree.

Unlike the version space candidate-elimination algorithm,

• ID3 searches a completely expressive hypothesis space (ie. one capable of expressing any finite discrete-valued function), and thus avoids the difficulties associated with restricted hypothesis spaces.
• ID3 searches incompletely through this space, from simple to complex hypotheses, until its termination condition is met (eg. until it finds a hypothesis consistent with the data).
• ID3's inductive bias is based on the ordering of hypotheses by its search strategy (ie. follows from its search strategy).
• ID3's hypothesis space introduces no additional bias.

ID3算法只有树的生成 故该算法生成的树容易过拟合

ID3 算法是建立在奥卡姆剃刀（用较少的东西，同样可以做好事情）的基础上：越是小型的决策树越优于大的决策树。

C4.5

C4.5 算法最大的特点是克服了 ID3 对特征数目的偏重这一缺点，引入信息增益率来作为分类标准。

这里需要注意，信息增益率对可取值较少的特征有所偏好（分母越小，整体越大），因此 C4.5 并不是直接用增益率最大的特征进行划分，而是使用一个启发式方法：先从候选划分特征中找到信息增益高于平均值的特征，再从中选择增益率最高的。 （source：https://zhuanlan.zhihu.com/p/85731206）

3. 决策树的剪枝

优化损失函数 并 考虑了减小模型复杂度

4. CART

CART的生成

对回归树用平方误差最小化准则，对分类树用gini index最小化准则，进行特征选择，递归构建二叉决策树

CART的剪枝

剪枝，形成一个子树序列

在剪枝得到的子树中交叉验证选择最优子树 平方误差或基尼系数最小的决策树被认为最优的决策树