使用KNN方法进行MNIST数据集分类
声明:本文的代码部分可以戳这里下载~
一、MNIST数据集
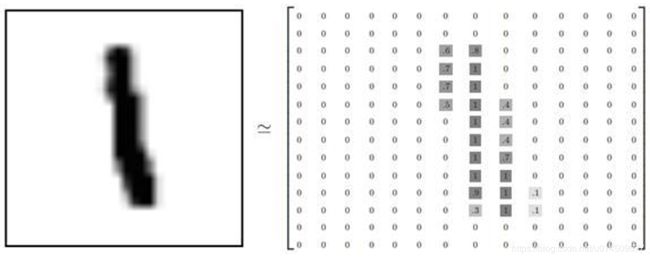
MNIST是深度学习的经典入门demo,他是由6万张训练图片和1万张测试图片构成的,每张图片都是28*28大小(如下图),而且都是黑白色构成(这里的黑色是一个0-1的浮点数,黑色越深表示数值越靠近1),这些图片是采集的不同的人手写从0到9的数字。TensorFlow将这个数据集和相关操作封装到了库中。
上图就是4张MNIST图片。这些图片并不是传统意义上的png或者jpg格式的图片,因为png或者jpg的图片格式,会带有很多干扰信息(如:数据块,图片头,图片尾,长度等等),这些图片会被处理成很简易的二维数组。
二、KNN算法
KNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。回到本文所述的实验中,即为在训练集中数据和标签已知的情况下,输入测试数据,通过计算训练样本和测试样本的曼哈顿距离,将测试样本的特征与训练样本中对应的特征进行比对,找到训练样本中与当前测试样本最为相似的前K个样本数据,则该测试样本对应的类别就是K个数据中出现次数最多的那个分类。算法的过程可以描述为:
1)计算测试样本与所有训练样本之间的曼哈顿距离;
2)对所求解的曼哈顿距离进行递增排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试样本的预测分类。
三、实验部分
1、加载mnist数据
import tensorflow as tf
import numpy as np
import random
from tensorflow.examples.tutorials.mnist import input_data
mnist=input_data.read_data_sets('MNIST_data',one_hot=True)2、设定参数
trainNum=60000 # 训练图片总数
testNum=10000 # 测试图片总数
trainSize=50000 # 训练时候用到的图片数量
testSize=5 # 测试时候用到的图片数量
k=4 # 距离最小的K个图片3、随机选取训练样本和测试样本
trainIndex=np.random.choice(55000,trainSize,replace=False)
testIndex=np.random.choice(testNum,testSize,replace=False)
print(trainIndex.shape,testIndex.shape)4、生成训练数据和测试数据
# 生成训练数据
trainData=mnist.train.images[trainIndex]
trainLabel=mnist.train.labels[trainIndex]
# 生成测试数据
testData=mnist.test.images[testIndex]
testLabel=mnist.test.labels[testIndex]
print('trainData.shape=',trainData.shape)
print('trainLabel.shape=',trainLabel.shape)
print('testData.shape=',testData.shape)
print('testLabel.shape=',testLabel.shape)
print('testLabel=',testLabel)5、设定参数,以便使用tensorflow进行运算
trainDataInput=tf.placeholder(shape=[None,784],dtype=tf.float32)
trainLabelInput=tf.placeholder(shape=[None,10],dtype=tf.float32)
testDataInput=tf.placeholder(shape=[None,784],dtype=tf.float32)
testLabelInput=tf.placeholder(shape=[None,10],dtype=tf.float32)6、计算每个训练样本和测试样本之间的曼哈顿距离。即: 。在本实验参数设置的条件下,将结果统计为5行500列的数组。
。在本实验参数设置的条件下,将结果统计为5行500列的数组。
f1=tf.expand_dims(testDataInput,1) # 用expand_dim()来增加维度,将原来的testDataInput扩展成三维的,f1:(?,1,784)
f2=tf.subtract(trainDataInput,f1) # subtract()执行相减操作,即 trainDataInput-testDataInput ,最终得到一个三维数据
f3=tf.reduce_sum(tf.abs(f2),reduction_indices=2) # tf.abs()求数据绝对值,tf.reduce_sum()完成数据累加,把数据放到f3中7、使用tensorflow来进行计算
with tf.Session() as sess:
p1=sess.run(f1,feed_dict={testDataInput:testData[0:testSize]}) # 取testData中的前testSize个样本来代替输入的测试数据
print(p1)
print('p1=',p1.shape)
p2=sess.run(f2,feed_dict={trainDataInput:trainData,testDataInput:testData[0:testSize]})
print('p2=',p2.shape)
p3=sess.run(f3,feed_dict={trainDataInput:trainData,testDataInput:testData[0:testSize]})
print('p3=',p3.shape)
print('p3[0,0]=',p3[0,0]) # 输出第一张测试图片和第一张训练图片的距离8、选择距离最小的K个图片
f4=tf.negative(f3) # 计算f3数组中元素的负数
f5,f6=tf.nn.top_k(f4,k=4) # f5:选取f4最大的四个值,即f3最小的四个值,f6:这四个值对应的索引
with tf.Session() as sess:
p4=sess.run(f4,feed_dict={trainDataInput:trainData,testDataInput:testData[0:testSize]})
print('p4=',p4.shape)
print('p4[0,0]=',p4[0,0])
# p5=(5,4),每一张测试图片(共5张),分别对应4张最近训练图片,共20张
p5,p6=sess.run((f5,f6),feed_dict={trainDataInput:trainData,testDataInput:testData[0:testSize]})
print('p5=',p5.shape)
print('p6=',p6.shape)
print('p5:',p5,'\n','p6:',p6)9、计算每个类型出现的频率
f7=tf.gather(trainLabelInput,f6) # 根据索引找到对应的标签值
f8=tf.reduce_sum(f7,reduction_indices=1) # 累加维度1的数值
f9=tf.argmax(f8,dimension=1) # 返回的是f8中的最大值的索引号
# 执行
with tf.Session() as sess:
p7=sess.run(f7,feed_dict={trainDataInput:trainData,testDataInput:testData[0:testSize],trainLabelInput:trainLabel})
print('p7=',p7.shape)
print('p7:',p7)
p8=sess.run(f8,feed_dict={trainDataInput:trainData,testDataInput:testData[0:testSize],trainLabelInput:trainLabel})
print('p8=',p8.shape)
print('p8:',p8)
p9=sess.run(f9,feed_dict={trainDataInput:trainData,testDataInput:testData[0:testSize],trainLabelInput:trainLabel})
print('p9=',p9.shape)
print('p9:',p9)10、为每一个测试样本做出最终的预测值
with tf.Session() as sess:
p10=np.argmax(testLabel[0:testSize],axis=1) # 如果p9=p10,代表正确
print(('p10:',p10))11、将测试样本的预测值和真值作比较,计算算法准确度
j=0
for i in range(0,testSize):
if p10[i]==p9[i]:
j=j+1
# 输出准确率
print('accuracy=',j*100/testSize,'%')四、实验优化建议
最终分类准确率不稳定且多次实验间分类准确率的精度差别巨大,这可能是由于以下两种原因造成:
①训练样本数目太少,导致分类器没有得到很好地训练
②测试样本采用的数目太少,分类结果不具有代表性
因此,在后期的改进实验中,可以考虑从这两方面考虑算法下一步的优化和改进。通过增加随机采样的训练样本数目或者增加测试样本数目,获得稳定且好的分类结果。