Union-Find 算法实现
Union-Find
问题描述:
给定一个n个序列的对象,有两种操作:
-Union command:连接两个对象;
-Find/connected query:两个对象是否连接(有路径)
算法实现方式
1.用一个数组保存着每个对象所在的connected component,这种方式可以快速进行FIND,但是在union操作时需要遍历整个对象数组
2.利用树的观点,在数组中保存每个对象节点的parent,这个每个connected component就是一棵树,这种方式union很高效,只需要更新相应节点的parent即可,但是在find的时候可能就会遍历整个树,特别是当一棵树比较高的时候。
3.在上述2中实现union(p,q)的时候,我们用一种特定的方式将p所在的树的置为q所在树的孩子,没有考虑到树的大小,就会导致严重失衡的情况。Weighted quick-union 引入一个新的数组来保存每棵树的尺寸,总是将小树链入到大树下,实现相对的平衡。
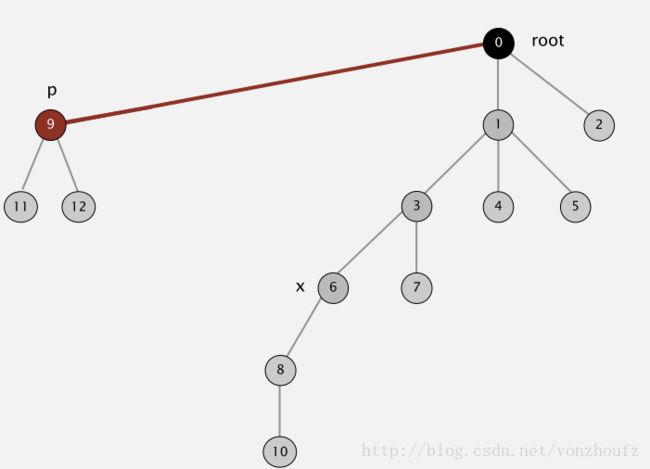
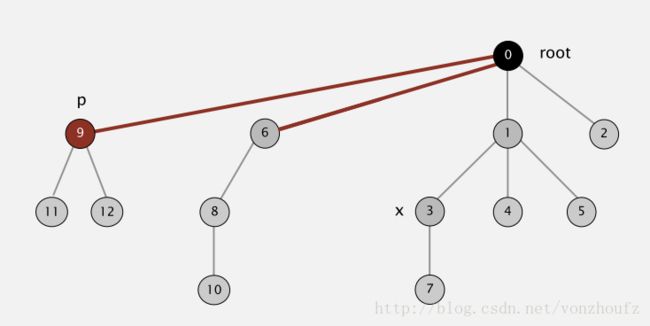
4.利用path compression进一步对上述算法进行优化,在每一次root操作的时候,不单单只是追溯查询一个节点的根,而是动态的将其根节点往上推进。从而使得 component tree 越来越平坦化。 如下要查询节点6的根节点,在查询的最后会更新6直接指向根节点。
接下来会把3,1分别指针指向root
具体代码
--------1
//这种方式可以快速判断是否相连,但是union操作需要遍历整个对象数组
public
class
QuickFindUF {
// 这个数组保存着这个N个节点的所在分组
private
int
[]
id
;
public
QuickFindUF(
int
n) {
id
=
new
int
[n];
for
(
int
i = 0; i < n; i ++) {
id
[ i] = i ;
}
}
public
boolean
find(
int
p,
int
q) {
return
id
[p] ==
id
[q];
}
// 连接p,q节点的时候,要将p所在component中的所有节点的id更新
public
void
union(
int
p,
int
q) {
int
pid =
id
[p];
int
qid =
id
[q];
for
(
int
i = 0; i <
id
.
length
; i++) {
if
(
id
[i] == pid)
id
[i] = qid;
}
}
}
-----------2
//这种方式可以快速实现俩个
public
class
QuickUnionUF {
// 这个数组保存着该对象的parent
private
int
[]
id
;
public
QuickUnionUF(
int
n) {
id
=
new
int
[n];
for
(
int
i = 0; i < n; i++) {
id
[i] = i;
}
}
// 辅助函数,追溯节点的n的根
private
int
root(
int
n) {
while
(n !=
id
[n])
n =
id
[n];
return
n;
}
public
boolean
find(
int
p,
int
q) {
return
root(p) == root(q);
}
// 连接p,q节点的时候,要将p的parent的parent更新为q的parent
public
void
union(
int
p,
int
q) {
int
parentp =
id
[p];
int
parentq =
id
[q];
id
[parentp] = parentq;
}
}
---------------3
public
class
WeightedQuickUnionUF {
private
int
[]
id
;
// id[i] = parent of i
private
int
[]
sz
;
// sz[i] = number of objs in subtree rooted at i
private
int
count
;
// num of components
public
WeightedQuickUnionUF(
int
N) {
count
= N;
id
=
new
int
[N];
sz
=
new
int
[N];
for
(
int
i = 0; i < N; i++) {
id
[i] = i;
sz
[i] = 1;
}
}
public
int
count() {
return
count
;
}
// 得到包含这个对象的component的ID,也就是根节点
public
int
root(
int
p) {
while
(p !=
id
[p])
p =
id
[p];
return
p;
}
public
boolean
connected(
int
p,
int
q) {
return
root(p) == root(q);
}
// 合并包含p,q的两个components,会考虑树的大小
public
void
union(
int
p,
int
q) {
int
rootP = root(p);
int
rootQ = root(q);
if
(rootP == rootQ)
return
;
if
(
sz
[rootP] <
sz
[rootQ]) {
id
[rootP] = rootQ;
sz
[rootQ] +=
sz
[rootP];
}
else
{
id
[rootQ] = rootP;
sz
[rootP] +=
sz
[rootQ];
}
}
}
----------------4
public
class
WeightedQuickUnionWitchPathCompression {
private
int
[]
id
;
// id[i] = parent of i
private
int
[]
sz
;
// sz[i] = number of objs in subtree rooted at i
private
int
count
;
// num of components
public
WeightedQuickUnionWitchPathCompression(
int
N) {
count
= N;
id
=
new
int
[N];
sz
=
new
int
[N];
for
(
int
i = 0; i < N; i++) {
id
[i] = i;
sz
[i] = 1;
}
}
public
int
count() {
return
count
;
}
// path compression实现在这里。
public
int
root(
int
p) {
int
root = p;
while
(root !=
id
[root])
root =
id
[root];
// 会将p以上的节点全部指向root
while
(p != root) {
int
newp =
id
[p];
id
[p] = root;
p = newp;
}
return
root;
}
public
boolean
connected(
int
p,
int
q) {
return
root(p) == root(q);
}
// 合并包含p,q的两个components,会考虑树的大小
public
void
union(
int
p,
int
q) {
int
rootP = root(p);
int
rootQ = root(q);
if
(rootP == rootQ)
return
;
if
(
sz
[rootP ] <
sz
[rootQ]) {
id
[ rootP] = rootQ;
sz
[rootQ] +=
sz
[ rootP];
}
else
{
id
[rootQ] = rootP;
sz
[ rootP] +=
sz
[rootQ];
}
}
}
备注:参考普林斯顿大学《算法,part I》