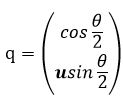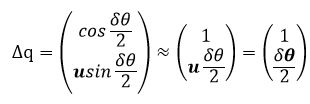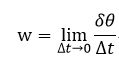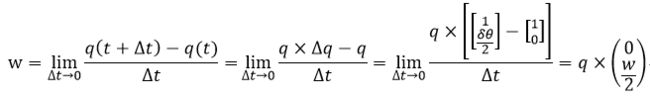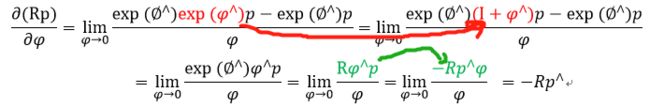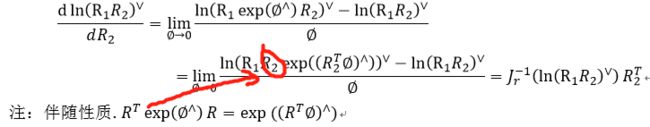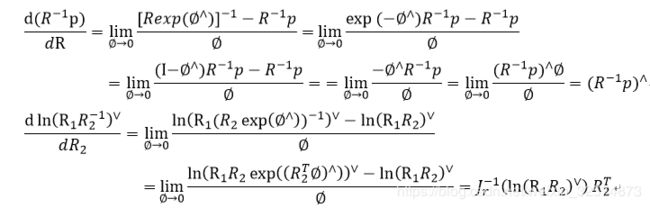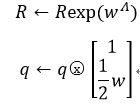从零手写VIO-第1讲
更多文章请关注微信公众号:SLAM之路
第1讲
1.What
2.How
3.Connection:
4.Why 紧耦合:
5.后续预备知识
6.作业
系列教程来自某学院,侵权删除。
学习完这一系列课程再去看VINS才能做到不吃力,不然直接撸网上的各种VINS解析完全云里雾里-_-!
1.What
VIO(visual-inertial odometry): 顾名思义即是以融合视觉及IMU实现里程计;
IMU(inertial measurement unit): 即惯性测量单元;
VO(visual odometry): 视觉里程计;
2.How
IMU:
1-典型6轴IMU以较高频率(≥100Hz)返回被测量物体的角速度与加速度;
2-易受温度、零偏、振动等因素干扰,积分得到的平移和旋转容易漂移;
VO:
1-图像形式记录数据,频率较低(15-60Hz居多);
2-通过图像特征点或像素推断相机运动;
3.Connection:
IMU和VO互为补偿,对方劣势即为本身优势;
IMU适合短时间、快速运动,VO估计IMU零偏减少发散和累计误差;
VO 适合长时间、慢速运动,IMU为VO提供快速运动时定位;
| 方案 |
IMU |
VO |
| 优势 |
1响应快 2不受成像质量影响 3角速度普遍比较准确 4可估计绝对尺度 |
1不产生漂移 2直接测量旋转与平移 |
| 劣势 |
1存在零偏 2低精度IMU积分易发散 3高精度价格贵 |
1受图像遮挡、运动物体干扰 2单目视觉无法测量尺度 3单目纯旋转运动无法估计 4快速运动时易丢失 |
松耦合:IMU和VO分别计算互不影响,典型方案卡尔曼滤波;
紧耦合:IMU和VO融合过程影响两者的参数(如IMU零偏和VO尺度),MSCKF/非线性优化;
4.Why 紧耦合:
1-单纯单目视觉(尺度不确定性)或IMU(零飘)都不具备估计pose能力;
2-松耦合VO中BA没有IMU信息,非最优;
3-紧耦合可以一次性建模所有运动和测量信息,更易达到最优;
5.后续预备知识
1-三维刚体运动常用坐标系:世界坐标系(W),IMU坐标系(I),相机坐标系(C);
状态量所用坐标系(1个)标识置于右上角,转换量所用坐标系(2个)置于右下角;
例![]() 表示从I到W系的变换矩阵;
表示从I到W系的变换矩阵;
2-四元数:+-*/模长逆共轭等运算(另开博文叙述);
3-单位四元数可表达任意三维旋转,且无奇异性;
4-轴角与四元数转换关系:某旋转运动旋转轴为单位向量u,绕该轴旋转角度为θ
当时间趋近于0,即旋转角度θ趋近于0,可得:
其中δθ的方向表示旋转轴,模长表示旋转角;
5-部分导数:
角速度:
旋转四元数对时间导数:
李代数so(3)导数:
在优化带有旋转的函数时,通常计算一个增量∅∈so(3),然后用它更新当前估计值:
Exp实现so(3)到SO(3)的映射,采用右乘;
6-常见雅克比(自变量为R)
旋转点的左扰动雅克比:
旋转点的右扰动雅克比:
旋转连乘的雅克比:
6.作业
使用右乘so(3)推导以下导数:
四元数或旋转矩阵可存储旋转变量,可以用计算出来的w对旋转进行更新,有以下两种方式:
请编程验证对于小量w=[0.01,0.02,0.03]T两种方法得到的结果非常接近,实践当中可视同为等同;
#include
#include
using namespace std;
#include
#include
#include "sophus/so3.h"
#include "sophus/se3.h"
int main(int argc, char ** argv)
{
//创建初始旋转向量,方向(0.707,0,0.707),旋转角度90度,并转化成旋转矩阵
Eigen::Matrix3d R=Eigen::AngleAxisd(M_PI/2,Eigen::Vector3d(0.707,0,0.707)).matrix();
Sophus::SO3 SO3_R(R);//USING rotation_matrix to create SO3
Eigen::Quaterniond q(R); //using quaterniond to create SO3
Sophus::SO3 SO3_q(q);
//when output SO3,using so3
cout<<"SO3 FROM MATRIX By rotation_vector1:"<<" "< 输出结果为: