目录
- topic
- 问题分析
*不可行思路
*可行思路 - 解决方案
- 代码与测试结果
- 优化&反思&扩展
- 最后
Topic
---- from leetcode题库,NO.576 Out of Boundary Paths
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ,你可以将球移到相邻的单元格内,或者往上、下、左、右四个方向上移动使球穿过网格边界。但是,你最多可以移动 **N **次。找出可以将球移出边界的路径数量。答案可能非常大,返回 结果 mod 109 + 7 的值。
示例 1:
输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6
解释:
示例 2:
输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12
解释:
说明:
- 球一旦出界,就不能再被移动回网格内。
- 网格的长度和高度在 [1,50] 的范围内。
- N 在 [0,50] 的范围内。
问题分析
乍一看,此问题显得略复杂,(反正我等小菜鸟是觉得好复杂,绝对不是leetcode标注的‘中等’难度TAT...)
复杂问题简单化,首先拆分问题:靠习惯性思维,我想想要用逻辑思维分析此问题,(用人话说就是想找个数学公式直接给算出来点啥)奈何,本人蠢,好像并没有搞出什么可行的计算方法。
首先,看到这个问题,第一感觉是迭代。当格子数大于1时,小球在格子里跑来跑去,完全可以乱跑,如果没有N的限制,小球完全可以永远在格子里转悠不出来(移动的步数无限大),步数无限大也就意味着路径无限多,(这特么是想要跑死我的小本本吗(⊙_⊙)...朕不干!)
恩,作为一个合格的心路历程小本本,错误的想法也应该如实记录下来。下面是乱入的错误思路—>
不可行思路
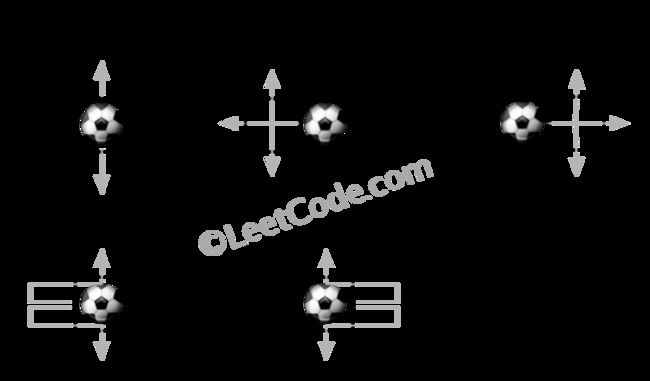
先甭管前面的跑法啦,把球扔到格子里的任意位置,我可以根据(i,j)和(m,n)的数学关系算出球在该位置一步就走出去的路径数。设路径数为x,根据路径数的不同可以把格子的空间分为三类:
- 格子的四角,一步出格子的x=2;
- 格子的四边上除去四角的格子,一步出格子的x=1;
- 格子的内部,一步压根儿就出不去,x=0
抽象成数学问题就是:
- i==0或者i==m-1,表示球在第一行或者最后一行
- 同理,j==0或者j==n-1,表示球在第一列或者最后一列
- 以上四个条件都不满足,说明球在大格子内部,一步出不去,需要迭代解决
上面三条,前两条都很好表示,宝宝都已经把前两步的代码写好了,第三条搞不定(=.=)关于第三条不成熟想法是:不论球在格子内部如何游走,想要出大格子,最后一步一定是从大格子四边上的某格子,一步跨出去的,跨出去的方向有四种,i=0可以向上跨,j=0可以向左跨,i=m-1可以向下跨,j=n-1可以向右跨。而小球任意位置的移动都可以抽象成这四种跨越方式,貌似可以用递归模型呀~迭代->递归,前两条所列的出大格子的方式可以作为递归的基例,那么最头疼的问题就是递归链条了!一眼看不出来该怎么迭代起来,(头疼TAT)那从数学归纳法的角度想想,要找到第x-1步到第x步之间的关系,也就是倒数第二步到最后一步的关系......
要不我把大格子拆分试试?比如说最后一步球在第一行某位置,那在倒数第二行时,我就当作第一行不存在,就相当于球从第二行向上跨越上边线出界啦,这样只需要将起始行加一就行,同理可以对另外三边做收缩处理~貌似可行,转念一想,大事不好!倒数第二步的时候球不一定是从第二行跨越到第一行啊,小球完全可以在第一行内部左右晃荡很久之后,突然心情一好,就出去啦!什么鬼!(摔笔)
噢,神呐,放过我吧,宝宝想不出来T_T,这小破球完全可以永远在格子里晃悠,爱出来不出来吧!
可行思路
以上,思路行不通T_T。。。
第二天,重新开始思考这个问题,重读题干,突然发现我忽略了一个重要参数N,N用来限制球在格子内移动的步数,只要步数有限,小球就不会永远在第一排晃悠啦\(≧≦)/。
所以问题的关键(或者难点),必然跟参数N有关,球移动的步数必须小于指定参数N(此处手动为N打光加欢呼特效~)
因此本题迭代过程中,我们关注的两个量,一个是计算结果--路径数,另一个就是移动的步数,一条路径上的移动步数由N来限定,就可以限定迭代的次数啦,即当移动步数超过N时,即刻返回0。
好像可以在上面失败的思路上引入步数限定参数来继续思考噢,BUT!本宝宝倔强!昨天都摔过笔了,不想再继续那个脑仁疼的思路了╭(╯^╰)╮哼!就要换个方向思考!(说白了就是自个儿怂,旧思路太复杂,八成是整不出来了,那就假装敖娇的放弃吧 ~~~如果有大神能按照上面我失败的思路成功迭代出看来,请让小弟膜拜一下,跪谢~~)
那么回归正题,开始新的方向思考~
大方向依旧是迭代。基例,好说~递归链条,昨天从后往前推失败了,那今儿从前往后推试试。但是一定记得要考虑步数<=N!
设路径数记录为x,x初值为0,每走成功一条路就给x加一。
设步数为steps,那么最开始start_step=0,中间的某一步start_step不一定为0,小球每走一步steps加一,则对于下一步来说就是start_step比上一步加了1,(终于找到简单的迭代单位啦~(≧≦)/~啦啦啦可喜可贺)且每走一步start_step要与N比较,一旦start_step要超过N,打住!此路可以舍弃了,给x返回0吧。
接下来考虑每一步的行走情况:无论小球在网格的什么位置,一旦它还能走下一步,它都有四种方式走,即上下左右四个方向,每个方向走一步后,我可以通过坐标和网格行列数的比较,判断出它这一步是否出界了,一旦出界,路径数计数x+=1,如果没出界,那就继续走下一步,形成递归。
思路看起来可行,着手形成解决方案~
解决方案
首先,定义变量:
- 输出的路径数x,初值为0,每行走一步计这一步之后所有的路径数的初值都是0,因此每一步的函数中都重新定义局部变量x=0;
- 每一步开始时走过的步数start_step,用于统计走过的总步数与N比较,来退出迭代,与历史值有关,因此需要通过参数传递来记录;
- m表示网格行数,n表示网格列数,由函数参数给出,且在递归过程不会改变;
- i表示小球横坐标,j表示小球纵坐标,随着小球的移动坐标值相应变化。
然后,分析一次移动的过程:
- 开始某次移动时,从本次移动开始至N步内成功出界的路径数为x,初始化x为0;
- start_step由参数传入,本次移动后步数需要加一,因此start_step先加一;
- 判断本次移动后总步数是否超过N,若超过N则从本次移动往后的所有路径全无效,直接返回可行路径数0(基例);
- 若本次移动后总步数不超过N则可以进行本次移动:本次移动有四种可能,方向分别为上下左右;
- 针对各方向移动的可能性做判断:如果一步移动后出界,则路径数x加一(基例);若移动后未出界,则可以更新坐标,继续下一次的移动,从而形成递归;
- 四个方向都判断完后,返回本次移动的所有成功出界的路径数x。
函数1:基例
对每次移动是否出界的判断可以写成函数形式:函数名为go1step(宝宝纯属在瞎起名字,回头改0.0);参数包括网格大小m,n、移动前坐标i,j和移动方向direction,用direction分别为1、2、3、4表示上下左右四种移动方向;返回值为0或1,若移动后出界返回1,若未出界返回0。
本函数先根据参数direction区分本次将要移动的方向,再根据方向和坐标判断是否会出界。以direction=1为例,小球从(i,j)第i行第j列向上移动,当且仅当小球当前位于网格第一排时才可能向上一步出界,因此判断i是否为0即可知道向上是否出界,若i==0返回1,否则返回0。其他三方向同理。
注意:网格内行列数从0开始计数,因此m行n列的网格的最下面一行是第(m-1)行,最右边一列是第(n-1)列。
函数2:递归
此函数用来表示一次移动的过程,作为递归函数:函数名为go2step(不走心的函数名again,很明显是根据第一个函数扒拉来的,好嘛,全通了之后再整理代码时再改~);参数包括网格大小m,n、移动前坐标i,j、总步数上限N和本次移动开始时已走过的步数start_step;返回值为本函数中的局部变量x,表示可行的总路径数。
本函数先判断这一步是否可以走:如果走过这一步之后总步数超过N,甭管这一步是否出得去,后面的所有走法都是不可行的,所以直接返回可行的路径数为0,此处是由总步数限制来结束递归的一个基例;如果走过这一步后总步数没超过N,那么恭喜你,噢不,恭喜球,可以继续往下走~
然后就是判断本次移动怎么走的问题啦:我们的目标是统计出所有可行的路径数,因此每走一步都要考虑四个方向的所有走法,所求的是各方向的可行路径和,因此每个方向得出的x都要累加。
对各方向的移动,先判断本次移动后是否会出界:若出界,则一种走法结束,路径数加一,此处为由主动出界来结束递归的一个基例;若不出界,则可以从本次移动后的坐标开始走下一步,下一步的走法跟本次移动一样,从而构成递归函数,只需要根据方向更新一下下一步的起始坐标即可,向上走时i减一,向下走时i加一,向左走时j减一,向右走时j加一。
以上,完成。
代码与测试结果
将上面的方案写成代码,再加上运行时间时间和测试用例打印,得到了本宝宝跑通的第一版代码:
#coding utf-8
import time
def go1step(m, n, i, j,direction): if direction==1: return 1 if i==0 else 0 elif direction==2: return 1 if i==m-1 else 0 elif direction==3: return 1 if j == 0 else 0 elif direction==4: return 1 if j == n-1 else 0 def go2step(m, n, i, j, N,start_step): x=0 start_step+=1 if start_step > N: return 0 #----up x+=1 if go1step(m, n, i, j,1)==1 else go2step(m,n,i-1,j,N,start_step) #----down x += 1 if go1step(m, n, i, j,2)==1 else go2step(m,n,i+1,j,N,start_step) #----left x+=1 if go1step(m, n, i, j, 3)==1 else go2step(m,n,i,j-1,N,start_step) #----right x+=1 if go1step(m, n, i, j, 4)==1 else go2step(m,n,i,j+1,N,start_step) return x t=time.time() print(go2step(1, 3, 1, 1, 2, 0)) print(time.time()-t) 运行代码,换几个测试函数试试,bingo,答案都正确~
愉快的把代码粘到leetcode提交代码,然而,leetcode提示我超出时间限制!
TAT...我还能怎样,尝试优化试试~
尝试优化
仔细一瞧,第一个函数完全可以不要,直接在第二个函数里替换成各方向的判断条件就好啦~
而且上面的函数名怪奇怪的,貌似第二个函数更适合较go1step噢(走一步,够直白哈哈哈哈哈嗝~)
另外代码结构不符合本宝宝严谨的作风,怎么可以没有main函数!
于是有了下面这版代码:
#coding utf-8
import time
def go1step(m, n, i, j, N,start_step): x=0 start_step+=1 if start_step > N: return 0 #----up x+=1 if i==0 else go1step(m,n,i-1,j,N,start_step) #----down x += 1 if i==(m-1) else go1step(m,n,i+1,j,N,start_step) #----left x+=1 if j==0 else go1step(m,n,i,j-1,N,start_step) #----right x+=1 if j==(n-1) else go1step(m,n,i,j+1,N,start_step) return x def main(): t=time.time() print(go1step(10,10,5,5,10,0)) print(time.time()-t,'s') if __name__ == '__main__': main() 再次运行leetcode给出的超时的测试用例,amazing!时间减少看不少呢~
满心欢喜再次去leetcode提交代码,然而现实依旧残酷,依旧超出时间限制=_=
优化&反思&扩展
优化
其实上面尝试优化的代码本质上并没有节省多少运行时间,改动函数格式并没有改变计算方法的时间复杂度和空间复杂度。
看提交记录中显示的共94个测试用例才通过了47个就超时了,估计后面的测试用例的网格更大,统计的最大移动步数更大,这样看来我这种一一迭代的算法可能就是无法满足本题的运算需求和时间限制的。
看来想要满足本题的要求,宝宝必须得寻求更优的算法才行,比如说以下思路:
- 在步数限制的倒数第二步时,即N-1步时,判断出本次移动将是最后一步,不再向各个方向都走,而是直接返回一步出界的方向数,此返回值可由坐标和网格边界直接判断出,x∈[0,4];
- 根据leetcode给出的hints:
Hint 1
WIll traversing every path is fesaible? There are many possible paths for a small matrix. Try to optimize it.
Hint 2
Can we use some space to store the number of paths and updating them after every move?
Hint 3
One obvious thing: ball will go out of boundary only by crossing it. Also, there is only one possible way ball can go out of boundary from boundary cell except corner cells. From corner cell ball can go out in two different ways. Can you use this thing to solve the problem?
- 第一条没懂啥意思:是否每条路径都可行?一个小矩阵有很多种可能的路径。试图优化它。?.?啥意思?是让我把大网格切成小矩阵吗?就算求出小矩阵的路径数也不知道该怎么组合起来呀;
- 第二条好像蛮有道理的,但宝宝不知道该怎么具体实施:我们能否用一些空间来存储路径数,然后在每次移动后更新它?大概意思就是用空间来换时间吧,宝宝是用x来计路径数的,而且每次移动都会重新初始化一个x,在完成本次移动后的所有路径后,局部变量x被释放,结果累加到上一步的x上。貌似有点浪费空间,但不考虑空间复杂度的话,我也不知道还能怎样来牺牲空间 换取时间=-=,求大神指点。
- 第三条貌似跟我前面那个没想通的思路有点像:一个很明显的事是:球只能通过越过边界来出界。同时,除去角落的格子,球只有一种可能的方式来从边界格子走出界。球从角落格子能有两种出界方式。能用这个来解决问题吗?这里所说的‘corner cell’就是我上面所说的‘四角格子’,‘boundary cell except corner cells’就是‘四边上除去四角的格子’,而且我也能区分出这三类格子,但是就是没想通怎么处理内部格子的问题。。。求大神指点。
反正宝宝是没想出别的啥可行的方案了=·=
反正不考虑时间问题的话宝宝的代码在自己的环境中也都能算出正确答案=·=
反正leetcode上这个题一共只有20个人提交成功了,加上我都只有105个人提交了代码呢=·=
瞬间感觉自己在leetcode排名第125哈哈哈哈哈哈哈嗝~
虽然宝宝知道,只是自我安慰>^<
总之,关于这个题目,宝宝目前就能解到这个地步啦~~剩下的。。。求大神指点。
反思
终于到了反思环节啦~终于到精髓了,同时,快结束啦~\(≧≦)/~
反思解本题的全部过程,前面一半时间是在走弯路,当然也不一定是弯路。Anyway,如果我一开始就想到正向的迭代方法并实施,可能花的时间会少很多。
由前面的不可行的思路可以看出,宝宝的思考方式还是逻辑思维优先,即使我知道所有的运算都是由计算机来完成的,依旧想要寻求数学公式来解决问题,可能还是因为并不擅长计算思维。
计算思维是人类的第三种思维特征:
- 实证思维:实验&验证,以物理为代表
- 逻辑思维:推理&演绎,以数学为代表
- 计算思维:设计&构造,以计算机为代表
计算思维是基于计算机的思维方式,抽象问题的计算过程,利用计算机自动化求解。
分析本题时,第一感觉就是要利用递归函数,大方向并没有错,却在抽象问题过程中比较吃力。第一次的思路是想要通过推理和演绎找出计算路径数的公式,然而即使知道要使用数学归纳法,也因为忽略了总步数参数N而导致推理失败。第二次的思路就是按照计算思维在分析问题了,却仍是抽象问题的过程比较费劲,而且最终抽象出的解法很简单,或者说就是无脑,只是简单的跑过所有的移动的可能性,从而统计总步数,导致在参数比较大时程序运行慢。
回顾这两种思维方式的产物,是不是两者相结合效果能更好呢?比如说优化方案中提到的,局部出界问题由推理和演绎直接算出总路径数,全局移动过程再采用设计和构造迭代的方法来实现;或者将m*n的网格分解为许多小矩阵,再由小矩阵之间的关系组合出全局的可行路线数。
即 实现逻辑思维与计算思维相结合才能更好的优化此问题的解决方案。
扩展
先甭管运行速度如何,反正现在是能够算出“N步之内出界的所有路径数”了,那么由此扩展,将题干改成“走N步出界的路径数”,也就很容易啦~
简单推理就知道:
N步之内出界路径数=N-1步之内出界路径数+N步出界路径数
因此,N步出界路径数可有下面代码实现:
def GoOutAtStepN(m, n, i, j, N): return go1step(m, n, i, j, N,0)-go1step(m, n, i, j, N-1,0) 当然,此解法的弊端依旧是时间复杂度太高,可能还有更优解法。不再深入,如果有大神实现了,望赐教。
最后
碎嘴诗的第一篇博客,啰哩叭嗦的,终于写完了,撒花~(≧≦)/~
宝宝知道,碎碎念对阅读者来说并不友好,坚持看到最后的都是真爱~么么哒~
趁着宝宝还有力气码字,就想要多记录下来一些,所以文中不仅有解题思路,也有不少宝宝的小情绪,谁让宝宝爱写日记呢,就当是技术文档与日记的结合吧~不过真的很累人诶,比手写日记累多啦
为了学习为了进步为了节约时间,以后还是少写这种长篇大论的碎碎念好了...恩,以后还是以整理学习笔记为主好啦,要精简!也方便自己回头查看~至于日记嘛,专门开一类文集写日记好啦~日记得设私密>^<
最后的最后,如果有幸能有大神看完这篇碎碎念,希望能针对本文的问题给出些意见建议,再次跪谢。