机器学习之回归篇(一)
一、综述
回归就是从一组数据出发,确定某些变量之间的定量关系式,也就是建立数学模型并估计未知参数。回归的目的是预测数值型的目标值,它的目标是接受连续数据,寻找最适合数据的方程,并能对特定的值进行预测。其中所寻求的方程叫做回归方程,求解回归方程,首先要确定模型,最简单的回归模型就是简单线性回归(例如y = kx + b),然后就是求回归方程的回归系数(即k和b的值)。
二、线性回归
线性回归的模型(数学表达式)定义为: $$ f(x) = \sum_\limits{i=1}^n \omega_ix_i + \omega_0=\omega_0+ \omega_1x_1 + \omega_2x_3+...+\omega_nx_n $$, 用矩阵表
示就是\(f(x)= XW\),其中\(X = \begin{bmatrix}1&x_1&x_2&...&x_n \end{bmatrix}, W = \begin{bmatrix}\omega_0\\\omega_1\\...\\\omega_n\\ \end{bmatrix}\),\(X\)为增广特征向量,\(W\)是增广权向量。线性回归就是求解增广权向量的过程。
2.1简单线性回归举例
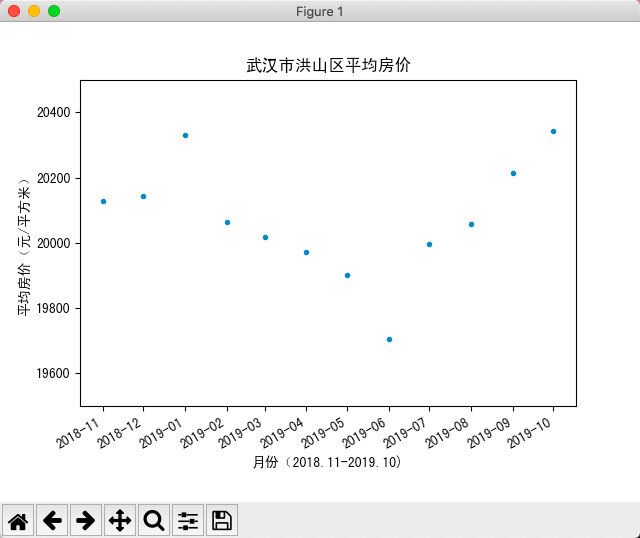
为了求出增广权向量,我们首先要进行取样,也就是从我们要研究的问题中取出一些具有代表性的数据。比如我要预测武汉大学附近的房价,那我首先就要找出武汉大学附近地区最近几年的房价数据(来源于:房天下)。这样我们就取得了一系列样本,这些样本数据包含两个维度,即时间和价格(实际上房价除了和这两个因素有关,还和地段、楼层、小区环境、物业等因素相关,这里我们主要是研究时间和房价的关系,所以价格应该指的是平均房价)。这样我们就可以建立一个二维平面直角坐标系,横轴表示时间,纵轴表示平均价格。如下图所示:
程序代码如下:
# -*- coding: utf-8 -*
import numpy as np
import pandas as pd
from datetime import datetime
from matplotlib import pyplot as plt
import matplotlib.dates as mdates
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']= False
x = ['2018-11','2018-12','2019-01','2019-02','2019-03','2019-04','2019-05','2019-06','2019-07','2019-08','2019-09','2019-10']
y = np.array([20128, 20144, 20331, 20065, 20017, 19972, 19902, 19706, 19997, 20057, 20213, 20341])
x = [datetime.strptime(d, '%Y-%m') for d in x]
plt.title("武汉市洪山区平均房价")
plt.ylim((19500, 20500))
plt.ylabel(u'平均房价(元/平方米)')
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))#设置时间标签显示格式
plt.gca().xaxis.set_major_locator(mdates.MonthLocator())
plt.plot(x,y,'.')
plt.xlabel(u'月份(2018.11-2019.10)')
plt.gcf().autofmt_xdate()
plt.show()
如果不能显示中文,请参考知乎第一条回答。
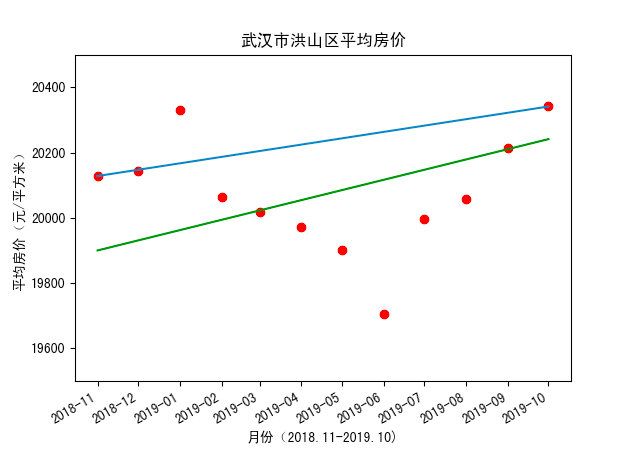
线性回归就是,求解一条形如y = kx + b的直线来去拟合这些散点。如下图,就有一蓝一绿两条直线对所有样本点进行了拟合。哪一条直线的拟合效果更好呢?
直观上来看,蓝线直接将第一个点和最后一个点连起来(事实上,代码里面我也是这么做的),绿线是将第五个点和倒数第二个点直接连起来(实际代码中,我并不是这样做的,只是图像恰好这么显示)。大部分点都在蓝线的下方,而绿线两侧的点大致均衡。所以,我们可以粗略地认为绿线的拟合效果要比蓝线好。这也就是高中数学(物理)中,经常讲到的拟合时要让样本点均匀分布在直线两侧(还有一条规则是,明显错误的数据点要舍弃)。
2.1线性回归的误差
线性回归,我们要找到一条最佳的拟合线,如何去判断拟合线是不是最佳呢?这里我们就要引出一个概念---误差。初中物理把误差定义为测量值和真实值之间的差异,在回归分析中,我们可以把误差粗略地定义为实际值减去预测值,数学表示为$$e = y_a-y_p(a表示actual,p表示predicted)$$,\(y_a\)为样本点的纵坐标,\(y_p\)为对应的直线上的点的纵坐标。(实际上,更为准确地定义是将误差用欧式距离来描述。线性回归中,就是找到一个直线,使得所有样本点到直线的欧式距离最小。)求解最佳拟合线,就是使得误差和\(\sum_\limits{i=1}^ne_i\)最小的直线的过程。在线性回归中,我们用损失函数\(J(w)\)来度量误差和的大小,通常情况下我们使用均方误差作为损失函数,数学表示为\(J(w)=\cfrac{1}{n}\sum_\limits{i=1}^n(y_a-y_p)^2\),对于均方误差,我们通常使用最小二乘法最小化损失函数。