决策树ID3、C4.5、CART、随机森林的原理与例子

（写在前面：作者是一名刚入学的模式识别专业的硕士生，第一次写博客，有错误的地方还请大家多多指教评论，一起交流呀~）

决策树的基本流程

①划分特征的选择（常见的选择方法有：信息增益、增益率、基尼指数，下文会详细介绍）

②划分停止准则：停止准则表示该节点不再划分，进而形成叶节点。
一般有几种情况：1) 当前节点包含的样本全部属于同一类别，则停止划分，形成叶节点；2) 当前属性集为空，或者所有样本在所有属性上取值相同，则无法划分，并将当前节点记为叶节点，类别为该节点所含样本数最多的类别；3) 当前节点所包含的样本集合为空，无法划分，则将当前节点设为叶节点，类别为该节点父节点所含样本最多的类别；4) 预先设定一个不纯度下降差的门限值。当候选分支使得节点的不纯度下降差小于这个门限，则停止分支，将当前节点记为叶节点，类别为该节点所含样本数最多的类别。（预剪枝）

③剪枝处理（预剪枝、后剪枝）
剪枝的基本思想是对相邻的叶节点（即有公共的父节点上），考虑是否应当消去它们。若消去它们后能引起令人满意的（即可容忍的）不纯度增长，那么就消去，否则，不消去。

预剪枝：通过设定某些规则提前停止树的分支而对树剪枝，一旦停止，节点就是叶节点。例如划分停止准则(4) 预先设定一个不纯度下降差的门限值。或定义一个样本阈值，当某个节点的样本个数小于该阈值时就可以停止决策树的生长等方法。

后剪枝：是基于训练集构建了一颗决策树后，利用测试集进行验证。若将某相邻的（即有公共的父节点上的）叶节点合并后，测试集误差比未合并前的小，则合并这些叶结点，否则，不合并。（此验证依赖于若干未经训练的样本集，且相比于预剪枝，这种方法更常用，因为在预剪枝的方法中要精确地估计何时停止树增长以及设定合适的阈值都比较困难）。

常见的决策树有：ID3、C4.5、CART——（这三种方法最大的区别在于：选择分裂属性的方法不同）

ID3

ID3算法的核心思想就是以信息增益来度量属性的选择，选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策空间。划分特征的选择方法：信息增益。首先，定义信息熵为：

其中，D为样本集合，共分为L类，$p_i$第i类样本数在样本集D中所占的样本数，i∈{1,2, …, L} 。Ent(D) 的取值越小，则D的纯度越高。

假定某个离散属性a有V个可能的取值$\{a^1,a^2,...,a^V\}$，若使用a来对样本D进行划分，则会产生V个分支节点。其中，第v个分支节点包含了D中所有在属性a上取值为$a^V$的样本，记为$D^V$。考虑不同的分支节点所包含的样本数不同，给分支节点赋予权重$|D^V|/|D|$，即样本数越多的分支节点的影响越大。因此用属性a划分样本集D所获得的信息增益为：

一般情况下，信息增益越大，代表使用属性a来划分所获得的纯度提升得越大。因此我们将选择$a_{\ast }=argmaxGain(D,a)$。

C4.5

ID3采用的信息增益度量存在一个缺点，它一般会优先选择有较多属性值的特征，为了避免这个不足，C4.5中是用信息增益比率(Gain_ratio)来作为特征选择分支的准则。且C4.5算法可用处理离散型特征和连续型特征。
信息增益率定义为：

其中，Gain(D, a)即为上述ID3方法中介绍的信息增益，而

IV(a)称为属性a的“固有值”，属性a所占数目越多，IV(a)的值通常会越大，可以避免了对属性值样本数目较多的特征更关注，但却会对属性值样本数目较少的特征更关注，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式方法：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的属性。

对于连续型特征，不能直接根据连续属性可取值来对结点划分，这种划分方法会增加树形的复杂度，也会带来较严重的过拟合。因此常见的做法是将连续属性离散化，一般情况下采用二分法对连续属性进行处理。

对于给定的样本集D以及连续属性a，假定a在D上出现了n个不同的值，先将这些值从大到小排序，排序后记为$\{a^1,a^2,...,a^n\}$。对相邻的属性值$[a^i,a^{i+1}]$来说，取二者的中间值，即会产生n-1个候选划分点$T_a=\{\frac{a^i+a^{i+1}}{2}|1\le i\le n-1\}$，则基于该候选划分点可将D分为子集$D_T^{-}$和$D_T^{+}$两部分，$D_T^{-}$表示的是在属性a上取值不大于T的样本，其中T∈$T_a$，$D_T^{+}$表示的是在属性a上取值大于T的样本。

则对信息增益(2)的式子稍作修改：

Gain(D, a, T)是指样本集D基于划分点T二分划分后的信息增益，因此我们可选取信息增益Gain(D, a, T)最大化后的划分点T作为属性a的离散值。

CART（classification and regression tree）

CART与前两种方法不同，它可以构建分类树和回归树。由于我们目前处理的任务是分类任务，因此这里只介绍分类树的构建。CART分类时，使用基尼指数（Gini）来选择最好的数据分割的特征，Gini描述的是纯度，与信息熵的含义相似。CART 也可用来离散型特征和连续型特征。Gini值的定义为：

Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此，Gini(D)越小，则数据集D的纯度越高。

采用与式（2）相同的符号表示，即属性a的基尼指数定义为

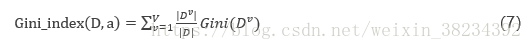
于是我们将在候选属性集合A中，选择使得划分后的基尼指数最小的属性作为最优划分属性，即：
$a_{\ast }=argminGini\_index(D,a)$。

CART算法同样适用于对连续型特征的处理，处理方式与C4.5算法类似，不同之处在于选择的方法为基尼指数，因此借鉴于式子（5）及式中符号意义，因此，式（7）可改：

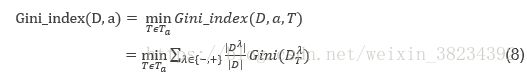
Gini_index（D, a, T）是指样本集D基于划分点T二分划分后的基尼指数。因此我们可选取Gini_index（D, a, T）最小化后的划分点T作为属性a的离散值。

CART决策树算法可视化过程

例子采用的是鸢尾花数据集，特征有4个，类别为3分类。

每个节点的输出值含义如下：用了哪个特征作为该节点划分feature，采用该特征划分下的基尼指数gini，该节点上的样本总数samples，归属该节点的类别。

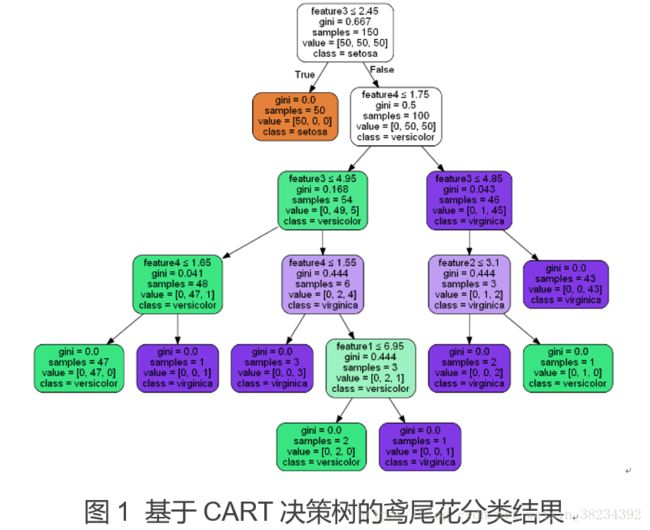
python代码如下：

from sklearn import tree #导入决策树
from sklearn.datasets import load_iris #导入datasets创建数组
from sklearn.model_selection import train_test_split
import sklearn.metrics as metrics

iris = load_iris() #导入数据
iris_data = iris.data #选择训练数组
iris_target = iris.target #选择对应标签数组
X_train, X_test, y_train, y_test = train_test_split(iris_data, iris_target, test_size=0.3)

clf = tree.DecisionTreeClassifier() #创建决策树模型
clf = clf.fit(X_train, y_train) #拟合模型

y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
print("Testing accuracy", clf.score(X_test, y_test))
cnames = list(['setosa', 'versicolor', 'virginica'])
print(metrics.classification_report(y_test, y_pred, target_names=cnames))

#import graphviz #导入决策树可视化模块
import pydotplus
from IPython.display import Image
data_feature_name = ['feature1', 'feature2', 'feature3', 'feature4']
data_target_name = ['setosa', 'versicolor', 'virginica']

dot_data = tree.export_graphviz(clf, feature_names=data_feature_name, class_names=data_target_name, out_file=None, filled=True, rounded=True, special_characters=True) #以DOT格式导出决策树
graph = pydotplus.graph_from_dot_data(dot_data)
img = Image(graph.create_png())
graph.write_png("iris.png")

随机森林

随机森林是由n颗决策树构建，且决策树之间是独立同分布的，具体流程如下：

① 给定训练集Training，测试集Testing，以及数据特征的维数F；
需给定的参数：森林中的CART决策树的数量T，每棵树的最大深度d，随机选择每个节点需要使用到的特征数量f（其中f<$f=\sqrt{F}$）。终止条件：到达节点上最少样本数阈值s，节点上最小的基尼指数阈值m。（根据实际情况终止条件还有其他可以选择，如上面决策树基本流程部分的划分停止准则）
② 对于第i颗树（i∈{1，2，…，T}）从训练集Training中随机地有放回的抽取与Training大小一样的数据集构成T(i)，从根节点开始训练。
③ 如果当前节点达到终止条件中节点上的样本数小于s，则设置当前节点为叶节点，对于分类问题，则返回该节点的样本数据集合中数量最多的那一类max_c作为当前节点的类别标签，而概率p则为max_c的数量占该节点所有样本数的比重。对于CART决策树算法，采用了基尼指数作为选择分裂属性的标准（对于离散型特征和连续型特征的选择方法已在上文中介绍，此处不再累赘），因此从f个特征中找出基尼指数最小的特征f(j)及其阈值th，小于阈值th的样本被划分到左节点，大于th被划分到右节点；若基尼指数小于指定阈值m，则终止分裂，同样返回类别标签和概率p。
④ 重复②③过程，直至所有节点被标记为叶节点。
⑤ 重复②③④过程，生成T颗决策树，即构建了一个随机森林。

随机森林分类效果（错误率）与两个因素有关：
①森林中任意两棵树的相关性：相关性越大，错误率越大；
②森林中每棵树的分类能力：每棵树的分类能力越强，整个森林的错误率越低。

例子：Adult数据集

（根据人口普查数据预测收入是否超过5万美元/年。也被称为“人口普查收入”数据集。）

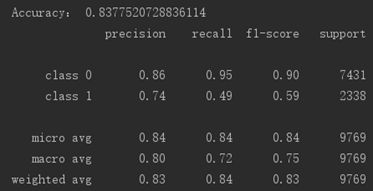
python代码如下：

# -*- coding: utf-8 -*-
from sklearn.ensemble import RandomForestClassifier #导入必要的库
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
import sklearn.metrics as metrics
from sklearn.model_selection import GridSearchCV
from sklearn import preprocessing
from sklearn.datasets import load_svmlight_file
import requests
from io import BytesIO

#load data 导入数据
r = requests.get('''https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary/a9a''')
x, y = load_svmlight_file(f=BytesIO(r.content), n_features=123)
x = x.toarray()

#split data training and testing
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

#randomForest
clf = RandomForestClassifier(n_estimators=50, max_depth=13, min_samples_split=50,
                                 min_samples_leaf=20, max_features=7, oob_score=True, random_state=10)
                                 #这里的参数设定可以用搜索法在一定范围内寻找最优参数
clf.fit(X_train, y_train.ravel())
#print(clf.oob_score_)#这里的袋外数据可作为模型的测试集等，有较大的作用

y_predict = clf.predict(X_test)
y_prob = clf.predict_proba(X_test)
print("Accuracy：", accuracy_score(y_test, y_predict) )
target_names = ['class 0', 'class 1']
print(classification_report(y_test, y_predict, target_names=target_names))
print("AUC score(Train): %f" % metrics.roc_auc_score(y_test, y_predict))

参考文献

[1]Zhou Z H, Feng J. Deep Forest: Towards An Alternative to Deep Neural
Networks[J]. 2017.
[2] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[3] 李航. 统计学习方法[M]. 清华大学出版社, 2012.
[4]PeterHarrington. 机器学习实战[M]. 人民邮电出版社, 2013.
[5] Google、百度学术