【2018.10.10】简单结构体二叉树及其应用

简单结构体二叉树及其应用

结构体二叉树的建立可以使用遍历或者递归，各有其特点，遍历代码复杂但是便于理解与阅读，递归理解更复杂，但是对应代码量要小很多

1.首先时画出我们一会要创建的二叉树。说是树可我更觉得他像一个根型结构。这个二叉树在前序遍历里的结构是：ABD##E##C#FG.去掉空树（#）就是ABDECFG.

首先是创建一个结构体，里面包含左右子节点。以及对应节点的数值。

typedef char Datatype;//这里我暂时用的char型，因为后面导入的是字符
typedef struct TNode{
	struct TNode * left;//左子节点
	struct TNode * right;//右子节点
	Datatype data;//节点数值
}TNode; 

接着是对二叉树创建，也是我自己琢磨最久的一个递归，难度在于每次创建二叉树后，需要返回，你已经使用的节点数，因为不是每个二叉树都是满的，存在单子节点。如同创建A的子节点时，我不仅需要得到返回B节点的地址，还需要得到，创建的以B为根时创建下面的树所消耗的数据个数，为此我们这里采用一个结构体作为返回值。就很好的解决了问题。

typedef struct{
	TNode * root;//返回创建的节点的地址
	int used;//告诉我，创建节点时消耗的数据个数
}Result;

接着我们开始创建这个二叉树。显示节点，然后是递归，我会尽量在代码里把注释写详细，但是还需要重复多看。

Result CreateTree(Datatype preorder[], int size)//创建二叉树，数值采用一个数组里的值
{
	if (size == 0)//size值为零，说明这是一个空树。
	{
		Result result = { NULL, 0 };//空树返回，NULL，使用了0个数据
		return result;
	}
	Datatype rootData = preorder[0];//根节点的赋值，取下数组的第一个值，赋给根。
	if (rootData == '#')
	{
		Result result = { NULL, 1 };//如果遇见#代表遇到了空树，返回NULL，但是用了一个数据’‘#，返回1
		return result;
	}
	TNode * root = CreateNode(rootData);//创建一个节点用root接收
	Result leftroot = CreateTree(&preorder[1], size - 1);//对A来说B是左子节点，但是对于D来书，B就是根，我是这么理解的。所以此处传数组第二个数，但是递归回去时，就是新的数组中的第一个数据。
	root->left = leftroot.root;//左树创建完毕
	Result rightroot = CreateTree(&preorder[1 + leftroot.used], size - 1 - leftroot.used);//同理创建右树，但是这里需要减去我们结构体中返回的使用数据的个数。
	root->right = rightroot.root;
	Result result = { root, 1 + leftroot.used + rightroot.used };
	return result;
}
static TNode * CreateNode(Datatype data)//创建节点
{
	TNode *node = (TNode *)malloc(sizeof(TNode));
	node->data = data;
	node->left = NULL;
	node->right = NULL;
	return node;
}

树就这样创建完毕里。接下来我们开始使用。我先把各个功能函数的声明在这里写下来。对照声明找每个功能函数的定义。

也就是我的头文件。Tree.h

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include 
typedef char Datatype;//定义数据类型为字符char型
typedef struct TNode{
	struct TNode * left;
	struct TNode * right;
	Datatype data;
}TNode; //创建结构体
typedef struct{
	TNode * root;
	int used;
}Result;//用于对二叉树创建时返回使用数据的个数，连同节点内容
Result CreateTree(Datatype preorder[], int size);//二叉树的创建
TNode * CreateNode(Datatype data);//节点的创建
void Preorder(TNode * root);//前序遍历（递归）包括中序遍历及后续遍历
int GetNodeSize(TNode *root);//获得节点个数（递归）
int GetLeafNodeSize(TNode *root);//获得叶子节点个数（递归）
int GetNokNodeSize(TNode *root, int k);//获得第K层节点个数
int GetTreehigh(TNode *root);//获得树高
TNode* Search(TNode *root, Datatype key);//搜索数据
void Mirror(TNode *root);//镜像二叉树（递归）
TNode * CommonAncestor(TNode * root, TNode *n1, TNode *n2);//获取两个节点的公共祖先节点
int IsbalanceTree(TNode * root);//判断一个二叉树是否是平衡二叉树



void Preorderloop(TNode * root);//前序遍历非递归
void Inorderloop(TNode * root);//中序遍历非递归
void Postorderloop(TNode * root);//后续遍历非递归
void Mirrorloop(TNode * root);//镜像二叉树非递归

因为在非递归函数中要使用到自定义类型栈这里加一下自定栈的头文件

Stack.h

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include 
typedef void * SDatatype;
#define MAX (100)
typedef struct {
	SDatatype arr[MAX];
	int top;//依旧描述大小，栈顶就是大小
}Stack;
void StackInit(Stack *p);
void StackDestroy(Stack *p);
void StackPush(Stack *p, SDatatype data);
void StackPop(Stack *p);
SDatatype StackTop(const Stack *p);
int StackSize(const Stack *p);
int StackEmpty(const Stack *p);

对应的二叉树函数的定义，我直接放全部Tree.c

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
#include "Tree.h"

Result CreateTree(Datatype preorder[], int size)
{
	if (size == 0)
	{
		Result result = { NULL, 0 };
		return result;
	}
	Datatype rootData = preorder[0];
	if (rootData == '#')
	{
		Result result = { NULL, 1 };
		return result;
	}
	TNode * root = CreateNode(rootData);
	Result leftroot = CreateTree(&preorder[1], size - 1);
	root->left = leftroot.root;
	Result rightroot = CreateTree(&preorder[1 + leftroot.used], size - 1 - leftroot.used);
	root->right = rightroot.root;
	Result result = { root, 1 + leftroot.used + rightroot.used };
	return result;
}
static TNode * CreateNode(Datatype data)
{
	TNode *node = (TNode *)malloc(sizeof(TNode));
	node->data = data;
	node->left = NULL;
	node->right = NULL;
	return node;
}
void Preorder(TNode *root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%c", root->data);
	Preorder(root->left);
	Preorder(root->right);

}
int GetNodeSize(TNode * root)
{
	if (root == NULL)
	{
		return 0;
	}
	return GetNodeSize(root->left) + GetNodeSize(root->right) + 1;
}
int GetLeafNodeSize(TNode *root)
{
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		if (root->left == NULL&&root->right == NULL)
		{
			return 1;
		}
		else
		{
			return GetLeafNodeSize(root->left) + GetLeafNodeSize(root->right);
		}
	}
}
int GetNokNodeSize(TNode *root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return GetNokNodeSize(root->left, k - 1) + GetNokNodeSize(root->right, k - 1);
}
int GetTreehigh(TNode *root)
{
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		if (GetTreehigh(root->left) > GetTreehigh(root->right))
		{
			return GetTreehigh(root->left) + 1;
		}
		else
		{
			return GetTreehigh(root->right) + 1;
		}
	}
}
TNode* Search(TNode *root, Datatype key)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == key)
	{
		return root;
	}
	TNode * node = Search(root->left, key);
	if (node != NULL)
	{
		return node;
	}
	node = Search(root->right, key);
	if (node != NULL)
	{
		return node;
	}
		return NULL;
}
void Mirror(TNode *root)
{
	if (root == NULL)
	{
		return;
	}
	TNode * node = root->left;
	root->left = root->right;
	root->right = node;
	Mirror(root->left);
	Mirror(root->right);
}
TNode * CommonAncestor(TNode * root, TNode *n1, TNode *n2)
{
	TNode *l1 = Search(root->left, n1->data);
	TNode *l2 = Search(root->left, n2->data);
	if (!l1&&l2)
	{
		return root;
	}
	if (l1&&!l2)
	{
		return root;
	}
	if (l1&&l2)
	{
		return CommonAncestor(root->left, n1, n2);
	}
	else
	{
		return CommonAncestor(root->right, n1, n2);
	}
}
int IsbalanceTree(TNode * root)
{
	if (root == NULL)
	{
		return 1;
	}
	int lb = IsbalanceTree(root->left);
	if (!lb)
	{
		return 0;
	}
	int rb = IsbalanceTree(root->right);
	if (!rb)
	{
		return 0;
	}
	if ((GetTreehigh(root->left) - GetTreehigh(root->right)) >= -1 && (GetTreehigh(root->left) - GetTreehigh(root->right) <= 1))
	{
		return 1;
	}
	else
	{
		return 0;
	}
}

非递归二叉树的函数

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
#include "Tree.h"
#include "Stack.h"

void Preorderloop(TNode * root)
{
	Stack stack;
	StackInit(&stack);
	TNode *node = root;
	TNode *top;
	while (!StackEmpty(&stack)||node != NULL)
	{
		while (node != NULL)
		{
			printf("%c", node->data);
			StackPush(&stack, node);
			node = node->left;
		}
		top = StackTop(&stack);
		StackPop(&stack);
		node = top->right;
	}
}//将printf转移到top命令下，即为中序遍历。
void Inorderloop(TNode * root)
{
	Stack stack;
	StackInit(&stack);
	TNode *node = root;
	TNode *top;
	while (!StackEmpty(&stack) || node != NULL)
	{
		while (node != NULL)
		{
			StackPush(&stack, node);
			node = node->left;
		}
		top = StackTop(&stack);
		printf("%c", top->data);
		StackPop(&stack);
		node = top->right;
	}
}
void Postorderloop(TNode * root)
{
	Stack stack;
	StackInit(&stack);
	TNode *node = root;
	TNode *top;
	TNode *last = NULL;
	while (node != NULL || !StackEmpty(&stack))
	{

		while (node != NULL)
		{
			StackPush(&stack, node);
			node = node->left;
		}
		top = StackTop(&stack);
		if (top->right == NULL || top->right == last)
		{
			printf("%c",top->data);
			last = top;
			StackPop(&stack);
		}
		else
		{
			node = top->right;
		}
	}
}
void Mirrorloop(TNode * root)
{
	Stack stack;
	StackInit(&stack);
	TNode *node = root;
	TNode *top;
	TNode *last = NULL;
	while (node != NULL || !StackEmpty(&stack))
	{

		while (node != NULL)
		{
			StackPush(&stack, node);
			node = node->left;
		}
		top = StackTop(&stack);
		if (top->right == NULL || top->right == last)
		{
			TNode * node = top->left;
			top->left = top->right;
			top->right = node;
			last = top;
			StackPop(&stack);
		}
		else
		{
			node = top->right;
		}
	}
}

测试我们的代码

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include "Tree.h"

void test()
{
	Datatype preorder[13] = { 'A', 'B', 'D', '#', '#', 'E', '#', '#', 'C', '#', 'F', 'G'};
	int size = sizeof(preorder) / sizeof(Datatype);
	Result rr = CreateTree(preorder,size);
	printf("%d\t%d\n", size, rr.used);
	Preorder(rr.root);
	printf("\n");
	Preorderloop(rr.root);
	printf("\n");
	Inorderloop(rr.root);
	printf("\n");
	Postorderloop(rr.root);
	printf("\n");
	Mirrorloop(rr.root);
	Preorder(rr.root);
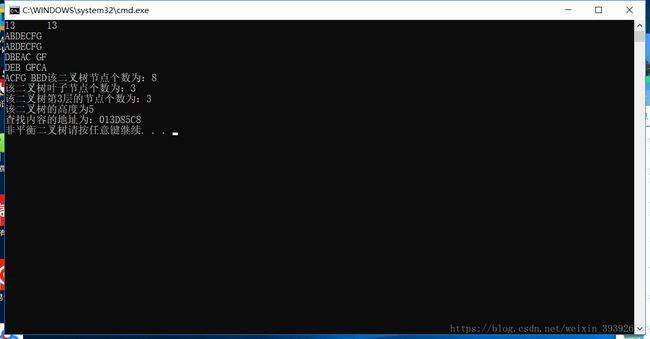
	printf("该二叉树节点个数为：%d\n", GetNodeSize(rr.root));
	printf("该二叉树叶子节点个数为：%d\n", GetLeafNodeSize(rr.root));
	int k = 3;
	printf("该二叉树第%d层的节点个数为：%d\n",k,GetNokNodeSize(rr.root,k));
	printf("该二叉树的高度为%d\n", GetTreehigh(rr.root));
	TNode *node = Search(rr.root, 'A');
	if (node == NULL)
	{
		printf("没找到\n");
	}
	else
	{
		printf("查找内容的地址为：%p\n", node);
	}
	if (IsbalanceTree(rr.root))
	{
		printf("平衡二叉树");
	}
	else
	{
		printf("非平衡二叉树");
	}
}
int main()       
{
	test();
}

这是我对结构体简单二叉树的部分总结。望各位大佬指正。