【R】ergm《随机指数图模型导论》读书笔记(一)
ERGM:《随机指数图模型导论》读书笔记
本来想搞一下tergm的,结果发现ergm都没搞明白,呜呜呜。
用的是格致的小绿皮~https://book.douban.com/subject/26985098/
- 第一章 网络分析方法的希望于挑战
- 历史与概念
- 统计网络模型的两个分支:
- 行动者为中心 actor-focuses: 解释和预测行动者的属性
- 自我中心网络egocentric network: 网络的形态解释中心个体的属性
- 整体网络whole network
- 关系为中心 tie-focused:解释和预测关系形成和关系模式
- 指数随机图模型ergm:
- 行动者为中心 actor-focuses: 解释和预测行动者的属性
- 统计网络模型的两个分支:
- 网络术语
- actors, nodes, vertices, individuals, members
- relations, ties, links, lines, edge
- 二分/加权
- 有向-arc/无向
- 二元组,三元组triads
- 历史与概念
- 第二章 统计网络模型
- 简单随机图
- 定义
- 一个简单随机图是在由n 个节点构成的所有可能网络中随机选择的网络,其中,网络中的每一条连线(联系两个节点)都以同样的特征概率发生。
- 简单随机图中关系发生的概率是网络中所观测的关系数占所有可能的关系数的比例。即网络密度(network density)。
- 网络密度公式:L/(n(n-1)/2)
- n 是网络中节点的数量,又称网络规模(network size)
- L是网络中边的数量
- 特征(实际观测网络与随机图相比)
- 网络成员在建立关系的倾向上并不是完全相同的,即非均匀性度分布(nonuniform degree distribution)
- 具有相似特征的行动者之间建立联系的概率往往要高于基于随机联系产生的概率,即同质性(homophily)
- "朋友的朋友也是我的朋友”发生的概率通常要高于随机发生的概率,即传递性(transitivity) -表现形式
- 二元组共享伙伴(DSP):一个二元组(连通或不连通均可),有多个其他的个体与这个二元组的成员均相连
- 边共享伙伴(ESP) :一个二元组(连通的),有多个其他的个体与这个二元组的成员均相连,用法是:该二元组有1个边共享伙伴、该二元组有2个边共享伙伴、有1个边共享伙伴的连通二元组有几个,有2个边共享伙伴的连通二元组有几个。
- 三元组(闭合三角形)
- 真实有向网络往往会比随机(有向)网络产生更多的互惠性 (reciprocity) 联系。(如 布莱恩<----->贝琪))
- 定义
- ergm的发展
-
(1) 简单随机图模型(simple random graph models) ;
-
(2) 二元独立性模型(dyadic independence models) ;
-
(3) 二元依赖性模型(dyadic dependence models) ;
-
(4) 高序依赖性模型(higher-order dependence models)
-
- 简单随机图
(这部分数学我一点也没看得懂呜呜呜,好惨哦,于是我看了斯坦福写了《social and economic network》的 matthew o jackson 教授的教程,强烈推荐一哈。
我自己做了字幕和讲稿的翻译-也发在油管上了:
- https://www.youtube.com/watch?v=Ma2Bj33Qemc:
- p1 随机指数图模型的优点在于: 1. 包括更多更丰富的网络局部特征(local features)和相关性 (dependencies) - 不仅是cluster, 三元组,而是细小到clique,isolate node。 2. 方便统计估计 - 随机指数家族有良好的统计性质
- p2 从历史的角度看:ergm曾被称为马尔可夫模型,p星模型。 (插播:哈哈哈哈intersting, 因为之前的模型都不够好,所以科学家搞了一堆hybrid model混血模型) 我们想要的是:link ij 形成的概率依赖于link jk 和 link lk(三元闭合)。但是这样面临了一个问题:一旦我们让边的形成相互依赖,那么以为着一切边的形成都是关联的correlated,边变成互锁的interlock,一条边影响它的邻居,它的邻居又反过来影响它(类似内生性问题??),于是我们面对的这个系统将是一个拥有大量相关性的系统。我们需要去识别整体的关联性。
- p3 一个简单的例子: 1. 网络的概率 等于 网络中形成的边数量 2. 网络的概率 等于 网络中形成的三元组数量 (试想:拥有相同的边的数量,而不通过三元组数量的两个网络)
- p4 边的似然,取决于节点的属性,也取决于节点是否有共同的邻居。
- p5 网络G的概率 依赖于 系数1*G拥有的边的数量 + 系数2*G拥有的三元组的数量 因为上述式子可能会出现负数,而概率不可能是负数,为了式子有更好的性质,所以加上exp,让图的概率可以一直是正的。
- p6 在 hammer sly 1971未发表的论文中,他指出:任何的网络模型,都可以表示为指数家族with 图中的统计上的加总。 (试想,假设你有一个很复杂的具体模型,你可以写上很多很多的统计量:边,三元组,二元组,clique,点的属性,出入度分布等等等等)
- p7 给定网络G的概率 等于 exp(系数1*G拥有的边的数量 + 系数2*G拥有的三元组的数量) 除以(我理解下是)所有的和G有相同的节点和属性的可能的网络的 exp(系数1*G拥有的边的数量 + 系数2*G拥有的三元组的数量) 的和。(I am not pretty sure...) p8 endos-renyi gnp 为例子,最后的s1(g)是statistic , L(g), g拥有的边的数量
- https://www.youtube.com/watch?v=1a0H9vnJMZs:
- p1 回顾一下,ergm模型由权重乘以统计量的和表示。这一形式使得我们能知道图里有什么特征,哪些特征是显著的,图形成的主要原因是什么。
- p2 florentine marriages(反之类似一个家族商业联姻网络) 这篇文章的想法:统计了一下florentine marriages里各种统计指标(如link,2-星,3-星,三角形),然后estimate图的概率表达式中有哪些系数(就是那些权重beta)和随机图比是显著的,然后就能知道是哪些指标造成了网络的形成?
- p3 estimate的算法逻辑:已知观测网络,在最大化该网络出现的概率时,这些系数是什么?(就是一个最大似然估计)
- p4 p5 florentine families的结果(应该是做完scaling的结果) 可以看到link的系数是-4.27,而标准差是1.13,也就是说在3个标准差外,并是负数,这说明,在这个网络中的link比起随机图来说是显著的少的,link并不是这个网络的主要特征。 类推,triad的系数是1.32,而标准差是0.65,也就是说在2个标准差外,并是正数,这说明,在这个网络中的triad比起随机图来说是显著的多的,triad是这个网络的主要特征。
- p6 ergm模型测量的难点在于计算标准化需要的那个分母,也就是所有可能出现的图的指标之和难以计算,因为图太多了,设想一个30个节点的图,就有2^(30*29/2)种图,这么多的图根本无法穷尽。那么抽样呢?所以科学家采用了MCMC方法在图上随机走动,并期待多次随机走动的得到的样本结果是具有代表性的,可以代表总体的图的情况。
- p7 然而,mcmc的方法并不是有效的,一项研究指出,对于一个稠密的网络,只有当网络中有相当多的独立link时,结果才会在想对较短的时间内收敛到精确的数字。这就意味着,似乎是从node-node的层次去理解这些网络,而不是从网络自身去理解,而从node-node层次去理解网络已有其他的技术,不能体现出ergm的长处,如果ergm不能从网络层面的特征理解网络,不能做到和其他现有技术不一样,那ergm有什么用呢?
- p8 例子:用mcmc方法,估计ergm模型中的系数,可能会出现的问题: 模拟一下网络,30个节点,10个独立,另外20个节点中,有65条link。这个网络出现的概率用ergm模型表示,beta1*link数 + beta2*isolate孤立点数。真实的beta1是-0.65,真实的beta2是-0.69。接下来用mcmc模拟估计两个beta的数值。模拟25次,每次中都有10000次mcmc run(样本数量10000)。结果显示:
- p9,p10 对link的beta1的估计一般,岁isolate点的beta2估计完全无效。
- p11 mcmc技术的estimate是不准确的。
- 第三章 建立一个有效的指数随机图模型(真本书2013年写的,比较古老,代码已经不能用了。。。。。就看看书吧,硬要看代码的去这里看:https://us.sagepub.com/en-us/nam/an-introduction-to-exponential-random-graph-modeling/book237737#description)
- 数据获取
- 数据探索
- 统计指标-整体:网络整体指标的summary(网络的规模、密度等)
- 图-整体:输出整体的网络图形
- 图-整体:输出网络中的最大成分(large component)-最大连通的节点集合
- 图-局部:节点的大小、形状-可以用节点大小反应度
- 统计指标-局部-数值:每个节点的平均连接数量(度的平均数)、度值出现的频次、三元组的分布情况
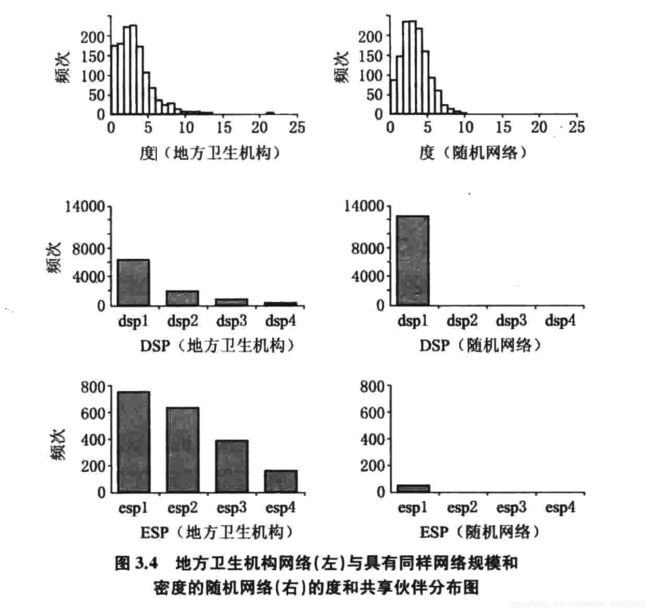
- 统计指标-整体-分布图:边共享伙伴(ESP)的分布
- 统计指标-整体-分布图:二元组共享伙伴(DSP) 的分布
- 地方卫生机构网络的成员具有多个边共享伙伴与二元组共享伙伴,这一点上,随机网络与观测网络具有显著不同,随机网络的特征是大量的节点仅具有单一的共享伙伴,具有多个共享伙伴的节点几乎没有。
- 混合矩阵(mixing matrix)-针对分类属性变量各层次之间各种可能的组合形式进行统计,从而检验相互连接的二元组(例如两个地方卫生机构之间的联系)在连接属性上存在的特征,例如.满足”两个地方卫生机构均执行了艾滋病筛查项目“条件的二元组有多少?或者满足”一个地方卫生机构位于密苏里州而另一个位于加利福尼亚州“条件的二元组有多少?这些混合矩阵将网络中属性的层级作为矩阵的行和列。矩阵单元格中的数字表示矩阵中具有对应行和列属性的相互连接的二元组数量。例如,在混合矩阵中,两个均执行营养项目的地方卫生机构之间相互连接的数量是1 812, 该数量显示在表3.2 中第二个混合矩阵的右下角。

- 计算“节点的连续型变量的特征”和“节点中心度”之间的相关性:例如对连续型变量进行观察,如检验辖区人口与中心度之间的相关性。相关系数的结果为0.21。该结果显示:地方卫生机构所在辖区的人口数量越多,该机构与其他机构之间建立的联系就越多。
- 用two-way-table探索网络属性(如机构领导人年龄和是否执行营养项目之间的关系)