LeetCode中等题
2 第二题 两数相加
问题描述:
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807
思路:
不断相加,存储在比较长的链表中,如果产生了进位,就从短的那个链表中偷一个结点来用。
示例代码:
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
L1 = l1
L2 = l2
lenthA = lenthB = 0
while L1: # 统计L1的长度
lenthA += 1
L1 = L1.next
while L2: # 统计L2的长度
lenthB += 1
L2 = L2.next
if lenthA < lenthB: # 置L1为长的那个 可以遍历到底
L1,L2 = l2,l1
else:
L1,L2 = l1,l2
temp = 0
res = L1 # 保存指向L1的指针
Node = L2 # 借L2一个结点
while L1:
if L2:
temp,L1.val = divmod(L1.val+L2.val+temp,10)
else:
temp,L1.val = divmod(L1.val+temp,10)
if not L1.next:
break
L1 = L1.next
if L2:
L2 = L2.next
if temp == 1: # 如果产生了进位,就需要之前从L2偷的结点了
Node.val = 1
Node.next = None
L1.next = Node
return res
3 第三题 :无重复字符的最长子串
题目描述:
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
思路:
从头到脚扫一遍,滑动着扫,设置start和end用来标志当前的下标。如果比maxs长,就更新maxs
解决方案1:
class Solution:
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
if not s:
return 0
start = end = 0 # 边界
maxs = 0 # 最大长度
current = 0 # 当前长度
for i,v in enumerate(s):
if not i:
end += 1
current = 1
maxs += 1
continue
if v in s[start:end]:
current = end-start
if maxs < current:
maxs = current
start = s.index(v,start,end) + 1
end += 1
current = end - start
continue
if v not in s[start:end]:
end += 1
current += 1
if maxs < current:
maxs = current
return maxs
发现解决方案1可以改进,解决方案2:
class Solution:
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
if not s:
return 0
start = end = 0
maxs = 0
current = 0
for i,v in enumerate(s):
if not i:
end += 1
current = 1
maxs += 1
continue
if v in s[start:end]:
current = end-start
if maxs < current:
maxs = current
start = s.index(v,start,end) + 1
end += 1
current = end - start
continue
if v not in s[start:end]:
end += 1
current += 1
if maxs < current: # 比第一个来了个优化。
maxs = current
return maxs
解决方案3(优化后的滑动算法(在字典里找效率高)):
class Solution:
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
if not s:
return 0
c_dic = {} #存放元素,下标对
start = 0 # 开始位置
end = 0 # 结束位置
current_len = 0 # 当前长度
maxs = 0 # 最大长度
for i,v in enumerate(s):
if not i: # 初始化
end += 1
current_len += 1
maxs += 1
c_dic[v] = i
continue
if v not in c_dic: # v不在c_dic时应该怎么做
end += 1
current_len += 1
c_dic[v] = i # 更新c_dic
continue
if v in c_dic: # v在c_dic应该怎么做
current_len = end - start # 先更新current值
if current_len > maxs:
maxs = current_len
end += 1
if c_dic[v] >= start: # 如果这个东西在当前序列
start = c_dic[v] + 1 # 则更新start
current_len = end - start
else: # 如果不在当前序列 则相当于v不在c_dic时
current_len += 1
c_dic[v] = i # 别管怎样都要更新c_dic
if maxs < current_len: # 防止出现全无重复的情况
maxs = current_len
return maxs
5 第五题 最长回文子串
问题描述:
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
输入: "cbbd"
输出: "bb"
思路:
这题只想到了爆破。就是不断的认为某个串是回文串,进行判断。这种时间复杂度高的吓人。
还有一种是manacher算法。没看太懂。先放在这儿,日后再说。
解决方案1(爆破):
class Solution:
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
if not s:
return s
max_len = len(s)
while max_len:
for i in range(len(s)):
if not i:
temp = s[:max_len]
else:
temp = s[i:i+max_len]
if temp == temp[::-1]:
return temp
if i + max_len == len(s):
break
max_len -= 1
解决方案2(manacher):
class Solution:
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
if not s:
return s
s = '#'+'#'.join(s)+'#'
mx = 0
lenth = len(s)
id = None
L = [0]*lenth
for i in range(lenth):
if mx > i:
L[i] = min(L[2*id-i],mx-i)
else:
L[i] = 1
while i-L[i]>=0 and i+L[i] < lenth and s[i + L[i]] == s[i - L[i]]:
L[i] += 1
if L[i] + i > mx:
mx = L[i] + i
id = i
maxs = max(L)
index = L.index(maxs)
newstr = s[index-maxs+1:index+maxs]
newstr = ''.join(newstr.split('#'))
return newstr
6 第六题 Z字形变换
对于第一行和最后一行,每个元素之间的差值是固定的,都是(numRows-1)*2。
对于其余的行,先差一个(numRows-i)*2 再差一个(i-1)*2。
这样就好写代码了。
解决方案:
class Solution(object):
def convert(self, s, numRows):
"""
:type s: str
:type numRows: int
:rtype: str
"""
res = ''
if not s:
return res
if numRows == 1:
return s
lenth = len(s)
for i in range(1,numRows + 1):
if i == 1 or i == numRows: # 处理第一行和最后一行
step = 2*(numRows-1)
if i == 1:
res += s[::step]
else:
res += s[numRows-1::step]
else:
stepA = (numRows - i)*2
stepB = (i - 1)*2
target = i-1 # 行数转下标
flag = True # 看看如何更新target
while target < lenth:
res += s[target]
if flag:
target += stepA
flag = False
else:
target += stepB
flag = True
return res
8 第八题:字符串转换整数 (atoi)
问题描述:
请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
说明:
假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围,qing返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
这题太长了不想看。。
总之就是,给你个字符串,你需要做如下操作:
先判空,如果空返回0 不空则继续以下操作
先把开头的空格去掉 去掉空格后如果为空,返回0 如果不空,继续以下操作
判断第一个字符是不是+-号,或者是数字,如果不是,返回0
如果第一个字符是+号,则取后面连续的res 如果res > 2147483647 则置为2147483647
如果第一个字符是-号,则取后面连续的res,如果res < -2147483648 则置为 -2147483648
如果是数字,还要判断res 只不过不用输出字符
解决方案:
class Solution:
def myAtoi(self, str):
"""
:type str: str
:rtype: int
"""
if not str:
return 0
t = str.strip()
if not t:
return 0
if not(t[0] == '+' or t[0] == '-' or t[0].isdigit()):
return 0
flag = ''
res = ''
if t[0] == '+' or t[0] == '-':
flag = t[0]
for i in t[1:]:
if not i.isdigit():
break
res += i
if len(res):
if flag == '-':
res = int(flag+res)
if res < -2147483648:
res = -2147483648
else:
res = int(res)
if res > 2147483647:
res = 2147483647
return res
return 0
else:
for i in t:
if not i.isdigit():
break
res += i
res = int(res)
if res > 2147483647:
res = 2147483647
return res
11 第十一题 盛最多水的容器
问题描述:
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
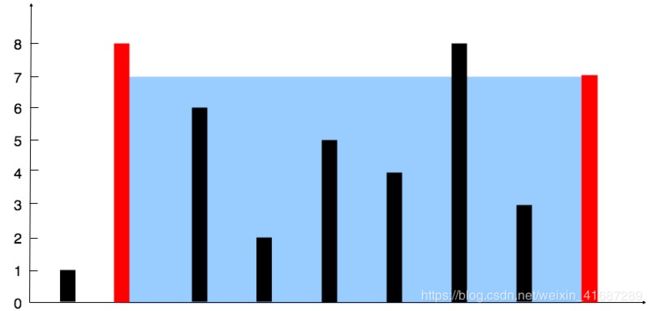
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
思路:
说实话这题把我绊住了。。
第一次,我想的是暴力法。
双层for循环,对于每一个i,遍历它与每一个j之间的面积,更新最大值。
这样跑出来的算法用leetcode的测试用例跑了2600ms
第二次,我改进了一下暴力法:
同样是双层for循环,不过对于值产生了选择,定住一个移动另一个,如果移动的那个移动后还变短了,
证明肯定不行,直接跳过。
这种改进之后的暴力法抛出了620ms 改进了很多,但是还是不行。
第三次,继续改进暴力法:
上面说过,定住一个移动另一个,那可不可以两边都移动呢?两边都移动的话就优化到O(n)了。
对的,可以两边都移动。但是一次只能移动一边。只移动矮的。为啥呢?因为矮的才是决定面积的
关键。为啥这么说?试想一下,如果你这已经是一个矮的了,定住矮的,移动高的,会有3种情况。
1、移动后比矮的还矮。(显然面积更小了)
2、移动后和矮的一样矮。(显然面积也变小了,因为虽然高度没变,但是宽度减小了)
3、移动后比矮的高。(但是没啥用啊,因为算面积要用矮的算,宽度也减小了)
这种方法循环10次才跑了5ms 也就是说一次仅仅是0.5ms
解决方案1(朴素的暴力法):
class Solution(object):
def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
maxs = 0
l = len(height)
for i in range(l-1):
for j in range(i+1,l):
if height[i] > height[j]:
low = height[j]
else:
low = height[i]
t = abs((j-i)*low)
if maxs < t:
maxs = t
return maxs
解决方案2(改进后的暴力法):
class Solution(object):
def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
maxs = 0
l = len(height)
for i in range(l-1):
left = height[i]
current_max = 0
for j in range(l-1,i,-1):
if current_max >= height[j]:
continue
current_max = height[j]
if left > current_max:
low = current_max
else:
low = left
t = abs((j-i)*low)
if maxs < t:
maxs = t
return maxs
解决方案3(终极解法):
class Solution(object):
def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
maxs = 0
l = len(height)
start = 0
end = l-1
while start != end:
if height[start] < height[end]:
low = height[start]
start += 1
else:
low = height[end]
end -= 1
t = (end-start+1)*low
if t > maxs:
maxs = t
return maxs
12 十二 整数转罗马数字
没啥难的,就不断的往下取余,整除就可以了。在我看来这个跟进制转换差不多。
解决方案:
class Solution(object):
def intToRoman(self, num):
"""
:type num: int
:rtype: str
"""
res = ''
while num >= 1000:
res += 'M'
num -= 1000
while num >= 900:
res += 'CM'
num -= 900
while num >= 500:
res += 'D'
num -= 500
while num >= 400:
res += 'CD'
num -= 400
while num >= 100:
res += 'C'
num -= 100
while num >= 90:
res += 'XC'
num -= 90
while num >= 50:
res += 'L'
num -= 50
while num >= 40:
res += 'XL'
num -= 40
while num >= 10:
res += 'X'
num -= 10
while num >= 9:
res += 'IX'
num -= 9
while num >= 5:
res += 'V'
num -= 5
while num >= 4:
res += 'IV'
num -= 4
while num >= 1:
res += 'I'
num -= 1
return res
15 十五 三数之和
问题描述:
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c
,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
实例:
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
分析过程:
首先想到了两数之和。但是两数之和的方法在这儿并不是很适用,为啥?
1、两数之和只有一种可能的情况,所以适用于用哈希表来解决问题。
2、三数之和,如果用hash表的话,也不是不行,就是效率低。想想看,如果用hash表,
需要两个循环,外层循环负责遍历nums列表,然后将当前遍历到的元素作为target
进行hash处理,而且nums列表是无序的,题目还要求了去重功能,而且添加进去的
结果列表还要是有序的,就算是无序,用hash表的方法已经是O(n^2)了,再加上要
对每个List的元素(也是个列表,只不过只有3个元素)进行排序,时间复杂度更高。
当然啦,用hash表的话比傻傻的写个O(n^3)+的代码还是要好很多的。
O(n^2)的复杂度还是过不了OJ的,这题显然不可能是O(n)能解决的,所以咱们得
想一个nlogn的解法。
3、我们可以先排下序,再进行处理。因为排序可以做到nlogn,就算咱们后续的处理算法是
o(n^2),那根据复杂度的计算规则,整体复杂度也就是个O(n^2),所以进行排序
是个一本万利的事儿。 然后我们就可以开始想算法了。外层的遍历target是逃不掉的
,所以我们得从内层循环上下功夫。还是那句话,两数之和时我们可以放心的用
hash表,为啥呢?因为如果要对nums表排序再处理的话,复杂度是大于o(n)的,不划
算,因为最快的排序算法也就是nlogn。但是对于双重for循环可不一样了,先排序,
复杂度没有超过n^2,而且排序后进行处理,可以使内层for循环小于o(n),所以总体
复杂度是优于O(n^2)的。我们的做法是用双指针。
仔细审题之后发现,作为外层循环遍历出来的target,应该具有唯一性。所以我们
在外层循环时可以跳过重复的target.(python模拟do-while)
然后对于内层循环,可以用双指针的方式来解决问题。具体怎么做呢?
对于每一个target ,设置它后面紧挨着的一个元素为left,然后nums的最后一个
元素设置为right,看一下target+left+right是不是能等于0.(这里有一点可
以优化一下:如果target直接>0了,那么怎么加都是出不了0的,所以可以直接结束
外层循环了(省了好多次),如果right直接<0了,那么也是不用处理的,因为这
样的话,怎么加也是到不了0的)
然后有的同学可能会问,为什么要把后面紧挨着的元素设置为left,而不是0号元素
呢?好问题。因为前面的元素设置为target过,我们已经把符合他们条件的所有3
个数的组合都搞过了,再把left设置从头开始只会徒增复杂度。
如果加起来不够0,说明和太小了,那么left指针需要右移,反之,right指针左移。
解决方案1(未进行优化版本):
class Solution:
def threeSum(self, nums):
nums.sort()
res = []
max_index = len(nums) - 1
used = set() # 我用了一个set来跳过前面用过的target
for i,v in enumerate(nums):
if v in used:
continue
used.add(v)
target = -v
left = i + 1
right = max_index
while left < right:
if nums[left] + nums[right] > target:
right -= 1
elif nums[left] + nums[right] < target:
left += 1
else:
res.append([v,nums[left],nums[right]])
while left < right: # 模拟do-while
left += 1
if nums[left] != nums[left-1]:
break
while right > 0: # 模拟do-while
right -= 1
if nums[right] != nums[right+1]:
break
return res
s = Solution()
print(s.threeSum([-2,0,0,2,2]))
解决方案2:(做了target优化):
class Solution:
def threeSum(self, nums):
nums.sort()
res = []
max_index = len(nums) - 1
used = set() # 我用了一个set来跳过前面用过的target
for i,v in enumerate(nums):
if v > 0:
break
if v in used:
continue
used.add(v)
target = -v
left = i + 1
right = max_index
while left < right:
if nums[right] < 0:
break
if nums[left] + nums[right] > target:
right -= 1
elif nums[left] + nums[right] < target:
left += 1
else:
res.append([v,nums[left],nums[right]])
while left < right: # 模拟do-while
left += 1
if nums[left] != nums[left-1]:
break
while right > 0: # 模拟do-while
right -= 1
if nums[right] != nums[right+1]:
break
return res
s = Solution()
print(s.threeSum([-2,0,0,2,2]))
16 十六 最接近的三数之和
问题描述:
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整
数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
实例:
例如,给定数组 nums = [-1,2,1,-4], 和 target = 1.
与 target 最接近的三个数的和为 2. (-1 + 2 + 1 = 2).
分析:
这题我首先想了个比复杂度O(n^3)强了一点的算法。如下:
先给数组排个序,耗时nlogn
再写了3层for循环,每一层都向后遍历,做了以下优化:
1、如果找到的cur_target 与target相同,就直接返回res
2、如果cur_closed与last_closed都比closed要大,而且cur_closed比
last_closed还要大,证明以后都不用循环了(因为再循环下去,cur_closed
更大,没有意义),直接break。
当然啦,有几点需要注意。
1、优化也是相对的,你再优化,量级也是O(n^3)
2、既然做了排序优化,那么为啥不能继续双指针呢?双指针法的话,可以把
O(n^3)直接降级到O(n^2),如果再做一些优化,这样更好。
然后开始双指针法:
1、针对外层循环的first值,要做去重处理,为啥?因为对于每一个双指针来说,
都已经筛选出了针对first的解,再跑一遍没意义,这样能省一大波计算。
2、针对双指针left和right,left的值是从first的下标+1开始的,为啥?
因为之前的值都是用过的first,用过了再用就重复了,所以没必要下标从
0开始。
3、针对left和right也要做去重处理。(模拟do-while)
4、当然啦,碰到closed=0或者说cur_target直接=target的,就可以直接
return res了,也能省一大笔开支。
解决方案(beat 93):
class Solution:
def threeSumClosest(self, nums, target):
nums.sort()
closed = abs(sum(nums[0:3]) - target)
res = sum(nums[0:3])
lenth = len(nums)-1
for index,first in enumerate(nums):
if index > 0 and first == nums[index-1]:
continue
left = index+1
right = lenth
while left < right:
cur_target = first+nums[left]+nums[right]
cur_closed = abs(cur_target-target)
if cur_closed < closed:
res = cur_target
closed = cur_closed
if closed == 0:
return res
elif cur_target-target < 0:
while left < right:
left += 1
if nums[left] != nums[left-1]:
break
else:
while left < right:
right -= 1
if nums[right] != nums[right+1]:
break
return res
s = Solution()
print(s.threeSumClosest([-1,2,1,-4],1))
print(s.threeSumClosest([-26,84,-85,2,99,42,-28,16,-97,-59,64,-67,-30,18,-15,-11,-60,-79,41,-29,49,-33,21,-8,-73,6,-31,31,-23,82,-34,12,86,38,-4,99,4,63,-13,-42,-4,89,88,-30,0,15,37,-95,-85,15,66,8,43,95,-76,75,-16,48,15,-82,56,83,91,81,-76,-29,7,-77,-42,39,-73,29,43,-60,21,-5,-3,1,32,34,-77,49,68,-1,-63,93,-20,-57,-65,53,23,96,79,87,-12,-18,51,39,-24,27,13,-55,-6,28,95,91,-71,77,49,-26,-17,-83,43,-86,28,20,64,-6,53,40,81,-30,-83,67,-3,25,37,54,95,14,84,-96,76,15,35,41,-86,33,10,-32,59,100,30,-9,58,-80,23,20,43,93,58,-26,37,44,-24,27,99,-46,-80,-85,-44,-45,-72,-32,33,-24,91,-67,75,-40,52,49,94,-10,82,-76,-92,58,18,-43,47,-75,-17,-30,-17,-57,37,51,-32,69,54,-71,-98,-74,-17,99,84,-67,80,-24,-100,98,19,99,-7,-98,-43,73,-97,-21,96,-44,59],-186))
17 十七 电话号码的字母组合
问题描述:
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:
尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
问题分析:
乍一看还不难。但是做起来发现不是这么回事儿。
我们先设置好返回值为res. 然后设置一个字典用于映射数字到字母。
然后写n个for循环进行遍历操作。遍历的对象是dict中数字映射的字母集合。
如果用for循环来进行遍历的话,的确可以做出来。但是我们会搞不清楚要写多少个for。
这就相当尴尬了。
怎么让计算机自己判断该写多少个for呢??或者说,怎么让计算机来模拟for循环呢?
我们想到了递归。
首先我们应该需要一个参数depth来设置递归深度,这样可以直观的看出来从哪返回。
然后我们还需要一个start参数用来标识当前递归处理的是digits中第几个数字对应的
字母集合。最后我们需要一个cur_res参数来记忆上层递归的“成果”。
什么是成果?举个栗子:
如果递归深度是2,digits是'23'那么第一层递归对给cur_res搞上'a' 或者'b'
或者'c',将这个成果,即'a','b',或者'c'传递给下层递归,拼接完成之后直接加入
res中,就没问题了。
另外,我们还需要对cur_res做一下回退处理。什么是回退?为什么我们要做回退呢?
想想看,如果你的最上层递归搞了'a',然后调用第二层递归搞了'd',然后开开心心的把
拼接成的'ad'加入了res,递归返回之后,cur_res在第一层的值是'a'嘛,然后你for循环
取出了'b',如果你不对'a'做回退处理,即删掉cur_res的最后一个值的话,就会造成
最上层递归此时变成了'ab' 的尴尬情况。
好了,优化之后就可以写代码了。
解决方案(beat 95+):
class Solution:
def letterCombinations(self, digits):
dicts = {
'2':'abc',
'3':'def',
'4':'ghi',
'5':'jkl',
'6':'mno',
'7':'pqrs',
'8':'tuv',
'9':'wxyz'
}
res = []
depth = len(digits)
def handle(start=0,depth=depth,cur_res=''):
if not depth:
return
cur_digit = digits[start]
cur_str = dicts[cur_digit]
for i in cur_str:
cur_res += i
handle(start+1,depth-1,cur_res)
if depth == 1:
res.append(cur_res)
cur_res = cur_res[:-1]
handle()
return res
s = Solution()
print(s.letterCombinations('23'))
18 十八 四数之和
问题描述:
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四
个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条
件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
实例:
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
思路:
其实这题思路并不难。双重for循环+双指针就可以解决。
有大致两种解法,递归和非递归。
递归实现可以将优化做的很好,所以时间复杂度大于非递归。但是缺点是空间复杂度太高了
非递归实现也能做部分优化,但是不可能像递归版一样面面俱到。所以性能差一点,
但是空间复杂度非常好。
下面我来说一下可以优化的点:
1、对nums的长度进行判断,小于4直接白扯。
2、对nums进行排序之后,对最小值*4,如果这个值大于target,那么直接返回
3、对nums进行排序后,对最大值*4,如果这个值小于target,那么直接返回
4、对运行中的长度进行判断。
比如我们用i,j,left,right分别代表按照次序的4个值的下标。如果下标i+3
大于了max_index,那显然是不行的。以此类推,j+2大于max_index也是不行的
left+1大于max_index也是不行的
5、对于重复值的跳过处理。如果我们之前处理过这个值,就可以直接跳过,
因为题目是要求去重的。而且跳过之后可以提高效率。
解决方案1(非递归版,beat75% 以及97%):
class Solution:
def fourSum(self, nums, target):
res = []
if len(nums) < 4: # 优化
return res
nums.sort()
max_index = len(nums)-1
if nums[0]*4 > target: # 优化
return res
if nums[-1]*4 < target: # 优化
return res
i = 0
while i < max_index:
if i+3 > max_index: # 优化
break
j = i+1
while j < max_index:
if j+2 > max_index: # 优化
break
left = j+1
if left+1 <= max_index and nums[i]+nums[j]+nums[left]+nums[left+1] > target:
break # 优化
right = max_index
while left < right:
cur_target = nums[i]+nums[j]+nums[left]+nums[right]
if cur_target == target:
res.append([nums[i],nums[j],nums[left],nums[right]])
while left < right:
left += 1
if nums[left] != nums[left-1]:
break
while left < right:
right -= 1
if nums[right] != nums[right+1]:
break
elif cur_target < target:
while left < right:
left += 1
if nums[left] != nums[left-1]:
break
else:
while left < right:
right -= 1
if nums[right] != nums[right+1]:
break
while j < max_index:
j += 1
if nums[j] != nums[j-1]:
break
while i < max_index:
i += 1
if nums[i] != nums[i-1]:
break
return res
s = Solution()
print(s.fourSum([-1,0,-5,-2,-2,-4,0,1,-2],-9))
解决方案2(递归 beat 95%):
class Solution:
def fourSum(self, nums, target):
def solution(left,right,N,last_target,last_res,res):
if right-left+1 last_target or nums[right]*N < last_target:
return
if N == 2:
while left < right:
cur_target = nums[left] + nums[right]
if cur_target == last_target:
res.append(last_res+[nums[left],nums[right]])
while left < right:
left += 1
if nums[left] != nums[left-1]:
break
while left < right:
right -= 1
if nums[right] != nums[right+1]:
break
elif cur_target < last_target:
while left < right:
left += 1
if nums[left] != nums[left-1]:
break
else:
while left < right:
right -= 1
if nums[right] != nums[right+1]:
break
else:
for i in range(left,right+1):
if i == left or (i > left and nums[i] != nums[i-1]):
solution(i+1,right,N-1,last_target-nums[i],last_res+[nums[i]],res)
res = []
max_index = len(nums)-1
nums.sort()
solution(0,max_index,4,target,[],res)
return res
s = Solution()
print(s.fourSum([-1,0,-5,-2,-2,-4,0,1,-2],-9))
19 十九 删除链表的倒数第N个结点
问题描述:
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
思路:
朴素思路:遍历一趟算出来需要从开头数第几个,然后再遍历一趟删掉它
高阶思路:设置快慢指针,快指针先跑N个,等快指针跑到底了,删除慢指针的下一个结点即可
解决方案1(朴素):
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
lenth = 0
H = head
while H:
lenth += 1
H = H.next
if lenth == 1:
return None
target = lenth - n
if not target:
return head.next
H = head
while target-1:
H = H.next
target -= 1
H.next = H.next.next
return head
解决方案2(高阶):
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
lenth = 0
H = head
while H:
lenth += 1
H = H.next
if lenth == 1:
return None
target = lenth - n
if not target:
return head.next
H = head
fast = head
while fast.next:
while n:
fast = fast.next
n -= 1
if fast.next:
H = H.next
fast = fast.next
H.next = H.next.next
return head
22 二十二 括号生成
问题描述:
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括
号组合。
实例:
例如,给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
解题思路:
分析这题之后,想到了数据结构课程中的判定是否是一个合格的括号表达式。
我一开始的解题思路是这样的:
1、写一个函数用来生成'('和')'的所有符合预定位数的组合
2、写一个函数用来判定生成的括号组合是不是合法
然后就开干了= = 不过只beat了20%
beat 20%当然是不行的,怎么着也得beat 90%把。我开始思考上个算法的缺点。
1、写函数来生成所有的组合再进行合法性判定有点冗余,会生成很多非法值,增大
时间复杂度。
解决方案:
1、在生成组合的时候,直接生成合法的括号表达式。
那么,如何生成合法的表达式呢?可以从咱们写的判定括号是不是合法的函数中抽象出来。
1、'('的总数和')'的总数相等,且都等于n
2、从前往后数,'('的个数总不小于')'的个数
所以我们就有了解法2
解决方案1(beat 20%):
class Solution:
def generateParenthesis(self, n):
res = []
def is_correct(s): # 判定是不是有效的括号组合
stack = []
for i,v in enumerate(s):
if not i:
if v == ')':
return False
stack.append(v)
else:
if v == '(':
stack.append(v)
else:
if not len(stack):
return False
else:
del(stack[-1])
if not len(stack):
return True
return False
def digui_generate(last_res='',depth=2*n): # 递归生成所有括号组合
if depth == 1: # 递归深度
for i in range(2):
if not i:
last_res += '('
if is_correct(last_res):
res.append(last_res)
last_res = last_res[:-1]
else:
last_res += ')'
if is_correct(last_res):
res.append(last_res)
else:
for i in range(2):
if not i:
last_res += '('
digui_generate(last_res,depth-1)
last_res = last_res[:-1]
else:
last_res += ')'
digui_generate(last_res,depth-1)
digui_generate()
return res
s = Solution()
print(s.generateParenthesis(3))
解决方案2(beat 98%):
class Solution:
def generateParenthesis(self, n):
def correct(cur_res,left,right,depth=2*n):
if not depth:
res.append(cur_res)
if left > right:
correct(cur_res+')',left,right+1,depth-1)
if left < n:
correct(cur_res+'(',left+1,right,depth-1)
res = []
correct('',0,0)
return res
s = Solution()
print(s.generateParenthesis(3))
24 二十四 两两交换链表中的节点
问题描述:
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
实例:
给定 1->2->3->4, 你应该返回 2->1->4->3.
仔细分析了一下,画个图就能一目了然。
我们需要关注的点:
1、leetcode给出的链表都是没有空头结点的链表,所以我们要跟严蔚敏老师那本
书中的算法区别开来,我们需要对开头2个节点进行初始化处理,然后我们发现
之后的节点要做的工作类似,于是做一个循环即可。
2、经过看图,我们需要注意以下几点:
a、注意处理空单链表,以及只有1个元素的单链表的情况
b、我们交换节点时,会破坏掉原有的指针,对于普通情况(除了前两个节点之外)
来说,我们需要作以下4步操作:
I、将当前处理组的第一个节点指向下一组的第一个节点
II、将上一组的第二个节点指向当前处理组的第二个节点
III、将当前处理组的第二个节点指向当前处理组的第一个节点
IV、更新上一组第二个节点的值为当前处理组的第一个节点(所谓的
上一组的第二个节点值,实际上就是处理过的序列的最后一个节点)
c、分析到这儿,可能会发现一个问题,在进行II时,初次执行循环时并没有
上一组的第二个节点啊?为啥?因为初始化开头俩节点的时候,由于没有
空的头节点,所以没有上一组的第二个节点这个东西。所以我设置了一个
first_flag用来标志是不是第一次处理通用的节点组。
解决方案(beat 97.5%):
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def swapPairs(self, head):
if not head or not head.next: # 如果链表为空,或者链表长度为1,直接返回head即可。
return head
cur_head = head # 当前的第一个指针
head = head.next # 为链表长度>1的情况设置head
cur_next = cur_head.next # 当前的第二个指针
first_flag = False
# 完成初始化操作
while cur_head and cur_next:
cur_head.next = cur_next.next
if not first_flag:
first_flag = True
last_next = cur_head
else:
last_next.next = cur_next
cur_next.next = cur_head
last_next = cur_head
cur_head = last_next.next
if cur_head:
cur_next = cur_head.next
return head
29 二十九 两数相除
问题描述:
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法
和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
实例1:
输入: dividend = 10, divisor = 3
输出: 3
实例2:
输入: dividend = 7, divisor = -3
输出: -2
说明:
被除数和除数均为 32 位有符号整数。
除数不为 0。
假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231 − 1]。本题中,
如果除法结果溢出,则返回 231 − 1。
思路:
这题的描述就挺坑。
如果对数学不太敏感的同学,看到不许用*/和%的时候,已经开始骂娘了。
其实我们可以用减法来模拟除法。不过这种效率很低的,我们只能在效率上动脑筋了。
我的做法是这样的:
用减法来模拟除法,过程不说了,很简单。
我们发现这样效率偏低。举个栗子,100除以3的话,用减法模拟除法需要运算33次,
但是如果100先减法减去3的10倍---30,能减3次,然后这里减一次30相当于减10次
3,所以每次累计10次减法。当100减去30不够减的了,再逐一减去3,如果不够减,
就可以直接返回了。
根据以上的思想,可以设计算法:
1、如果除数=0,那么直接返回-1
2、返回的值的范围应当在-2^31到(2^31)-1之间。如果不在这个区间内,直接返回
(2^31)-1
3、对于被除数和除数,为了归一化计算,我们设置了两个mirror来存储他们的绝对值,
用绝对值来进行计算。完事儿之后统一对cont的符号进行处理。
4、我们设置了一个bonus来对除数应当乘以多少倍进行探测。然后在处理过程中
逐渐降低bonus的数值以完成运算。
解决方案:(beat 97.5% 98.8%)
class Solution:
def divide(self, dividend, divisor):
if not divisor:
return -1
dividend_mirror = abs(dividend)
divisor_mirror = abs(divisor)
bonus = 0
while divisor_mirror*(10**(bonus+1)) < dividend_mirror:
bonus += 1
cont = 0
while bonus >= 0:
while dividend_mirror >= divisor_mirror*(10**bonus):
cont += 10**bonus
dividend_mirror -= divisor_mirror*(10**bonus)
bonus -= 1
if dividend*divisor < 0:
cont = -cont
if cont <= 2147483647:
return cont
return 2147483647
s = Solution()
print(s.divide(-2147483648,1))
四十三 字符串相乘
首先说一下,leetcode真是人心不古啊。。
我想破头也没想明白python进40ms的是啥算法。
闹了半天人家忽视规则直接eval的。
233333
问题描述:
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,
它们的乘积也表示为字符串形式。
示例:
输入: num1 = "2", num2 = "3"
输出: "6"
示例2:
输入: num1 = "123", num2 = "456"
输出: "56088"
说明:
num1 和 num2 的长度小于110。
num1 和 num2 只包含数字 0-9。
num1 和 num2 均不以零开头,除非是数字 0 本身。
不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
思路:
模拟小学的时候学过的乘法规则列竖式。
14*13 = 4*3 + 10*3 + 10*4 + 10*10 = 4*3*10^0 + 3*1*10^1 + 4*1*10^1 + 1*1*10^(1+1)
对于14和13来说,
14中,1的权重是1乘以10 4的权重是4*10的0次方。
13跟14差不多。
然后把所有的相乘再相加即可。
代码:
class Solution:
def multiply(self, num1: str, num2: str) -> str:
self.list1 = self.split_num_list(num1.strip("\""))
self.list2 = self.split_num_list(num2.strip("\""))
res = 0
for value,beishu in self.list1:
for value1,beishu1 in self.list2:
res += value*value1*10**(beishu+beishu1)
res = str(res)
return res
def split_num_list(self,num):
highest = len(num) - 1
res = []
for i,v in enumerate(num):
res.append((int(v),highest-i))
return res
槽点:
太久没刷leetcode了,都忘了leetcode不用自己输出了
567 五百六十七 字符串的排列
问题描述:
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,第一个字符串的排列之一是第二个字符串的子串。
示例:
输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").
输入: s1= "ab" s2 = "eidboaoo"
输出: False
注意:
- 输入的字符串只包含小写字母
- 两个字符串的长度都在 [1, 10,000] 之间
思路:
看到这种排列的题,就要注意它考察的并不是排列,为啥呢?因为排列复杂度太高了。
那怎么办呢?是否包含排列之一,也就是说要注意两点:
1、字母种类相同
2、字母数量相同
所以我们可以把s1转换成一个字母:个数的字典d1。
然后遍历字符串2的每一个与字符串1长度相同的字串,每次都生成一个字典d2,判断字典d1和字典d2是否相等。
相等即返回True
根据这个算法写出了代码。
但是执行效率稍微低一点。思考后发现,在遍历字符串2的与字符串1长度相同的字串时,
相邻两次的字串差别不大。比如字符串s2是"abcdefg" 字符串1长度是4.
那么第一次遍历s2中的字串是abcd 第二次是 bcde 少了a,多了e。
这样的话我们只需要更新a和e这两个开头和结尾的值就可以了,大大提高了效率。
由此给出了算法2
解决方案1:
class Solution(object):
def checkInclusion(self, s1, s2):
"""
:type s1: str
:type s2: str
:rtype: bool
"""
d1 = {}
for i in s1:
if i in d1:
d1[i] += 1
else:
d1[i] = 1
len_1 = len(s1)
len_2 = len(s2)
for i in range(len_2-len_1+1):
d2 = {}
for j in s2[i:i+len_1]:
if j in d2:
d2[j] += 1
else:
d2[j] = 1
if d1 == d2:
return True
return False
s = Solution()
if s.checkInclusion('a','ab'):
print(True)
else:
print(False)
解决方案2:
class Solution(object):
def checkInclusion(self, s1, s2):
"""
:type s1: str
:type s2: str
:rtype: bool
"""
d1 = {}
for i in s1:
if i in d1:
d1[i] += 1
else:
d1[i] = 1
len_1 = len(s1)
len_2 = len(s2)
d2 = {}
s2_mirror = s2[:len_1]
for i in s2_mirror:
if i in d2:
d2[i] += 1
else:
d2[i] = 1
if d1 == d2:
return True
elif len_1 >= len_2:
return False
low = s2[0]
high = s2[len_1]
for i in range(len_1,len_2):
if s2[i-len_1] not in d2:
d2[s2[i-len_1]] = 1
elif d2[s2[i-len_1]] > 1:
d2[s2[i-len_1]] -= 1
else:
del(d2[s2[i-len_1]])
if s2[i] not in d2:
d2[s2[i]] = 1
else:
d2[s2[i]] += 1
if d1 == d2:
return True
return False
s = Solution()
if s.checkInclusion('rvwrk','lznomzggwrvrkxecjaq'):
print(True)
else:
print(False)
"rvwrk"
"lznomzggwrvrkxecjaq"