1_线性回归算法梳理

机器学习基本概念

1.监督学习：

我们给算法一个数据集，这个数据集是由多个“正确答案”组成。例如：在房价估计的例子，我们给出一系列房子的数据，即房子的实际售价，运用学习算法，算出更多的正确答案。例如预计新房子的价格。

对比：
监督学习的数据集中每个数据已经标明是什么属性，清楚知道训练集对应的正确答案。但是无监督学习没有标签。

2.无监督学习：

没有任何的标签或者是有相同的标签或者就是没标签。所以我们已知数据集，却不知如何处理，也未告知每个数据点是什么。针对数据集，无监督学习算法能判断出数据有两个不同的聚集簇。

对比：
监督学习的数据集中每个数据已经标明是什么属性，清楚知道训练集对应的正确答案。但是无监督学习没有标签。

3.泛化能力：

是指机器学习算法对新样本的适应能力,学习的目的是学到隐含在数据对背后的规律，对具有同一规律的学习集以外的数据，对其他样本的适应能力，称为泛化能力。

4.过拟合：（overfitting）

过度拟合，例如学习器把训练样本自身的一些特点当成了所有潜在样本都有的一般性质，导致泛化能力下降。
处理：
1.丢弃一些不能帮助我们正确预测的特征；
2.正则化，保留所有特征但减少参数的大小。

5.欠拟合：（underfittin）

训练样本的一般性质未学好，学习能力低下造成的。
处理：添加特征项

6.交叉验证：

是用来验证分类器的性能一种统计分析方法，基本思想是把在某种意义下将原始数据（dataset）进行分组，一部分做为训练集（training set），另一部分做为验证集（validation set），首先用训练集对分类器进行训练，在利用验证集来测试训练得到的模型（model），以此来做为评价分类器的性能指标。

线性回归的原理

回归问题：是指根据之前的数据预测出一个准确的输出值。

线性回归损失函数、代价函数、目标函数

损失函数： 针对单个样本的误差

代价函数： 一般针对总体误差，用来衡量模型的拟合程度

目标函数： 带有正则项的代价函数，
等于经验风险+结构风险（也就是Cost Function + 正则化项）。

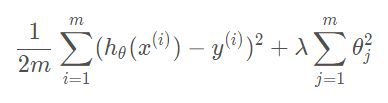
优化方法

1.梯度下降法：

梯度下降是一个用来求函数最小值的算法
梯度下降背后的思想是：开始时我们随机选择一个参数的组合(?0,?1,…,??)，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

梯度下降算法：

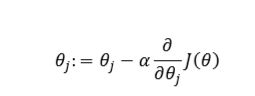
• 如果学习速率?太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。
• 如果?太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果?太大，它会导致无法收敛，甚至发散。

随着梯度下降法的运行，你移动的幅度会自动变得越来越小，直到最终移动幅度非常小，收敛到局部极小值。

2.牛顿法：

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x)导 = 0的根。牛顿法最大的特点就在于它的收敛速度很快。
通过泰勒展开，可以得到了一个递归方程：

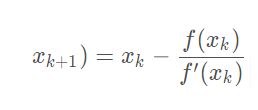
我们可以通过迭代的方式不断让x 趋近于x∗从而求得方程f(x) 的解。如图所示：

对于最优化问题： 对于最优化问题，要求代价函数最小值，而在其极值点处有一个特性就是在极值点处函数的一阶导数为0。因此我们可以在一阶导数处利用牛顿法通过迭代的方式来求得最优解，即相当于求一阶导数对应函数的根。

3.拟牛顿法：

拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。

线性回归的评估指标

1.SSE（误差平方和）

SSE=∑(y - f)2

同样的数据集的情况下，SSE越小，误差越小，模型效果越好。随着样本增加，SSE必然增加，也就是说，不同的数据集的情况下，SSE比较没有意义。

2.MSE（均方误差）

MSE=1/n*∑(y - f)2

MSE是SSE除以样本数量n，使其与样本数n无关。

3.R Squared（R方）

R2=1- ∑(y - f)2 / ∑(y - y平均)2

是衡量线性回归方法最好的指标，分母是原始数据的离散程度，分子为预测数据和原始数据的SSE，二者相除可以消除原始数据离散程度的影响。
R2 <=1，而且越大越好

sklearn参数详解

•	函数：
sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

•	参数：
(1)fit_intercept:默认为True，是否有截距b，如果没有则直线过原点。

(2)normalize:默认是False，是否将数据标准化。
 
(3)copy_X:默认为True，当为True时，X会被copied,否则X将会被覆写.。（即经过中心化，标准化后，是否把新数据覆盖到原数据上）。
 
(4)n_jobs:整型， 默认为1，计算时设置的任务个数(number of jobs)。如果选择-1则代表使用所有的CPU。这一参数的对于目标个数>1（n_targets>1）且足够大规模的问题有加速作用。

•	属性
coef_:数组(n_features)或(n_target,n_feature)线性回归问题的估计系数
intercept_:数组,线性模型中的独立项
 
•	方法
fit(X,y)拟合线性模型
get_params([])获取估算器参数
predict(X) 使用线性模型预测
score(X,y)

from sklearn import linear_model #调入库
reg=linear_model.LinearRegression() #建立模型
reg.fit([[0,0],[1,1],[2,2]],[0,1,2])#用线性回归器拟合三个点
reg.coef_ #返回线性方程系数