【推荐系统】Collaborative Filtering 协同算法 -- 一种用户评分预测方法 手算+例子应用
Collaborative Filtering 协同算法 – 一种用户评分预测方法
关键词:协同算法应用,Collaborative Filtering 例子,广告推荐,推荐系统算法,机器学习
1. 什么是协同算法
简单来说就是通过分析与目标用户相似的人群的行为,从而分析出目标的行为。
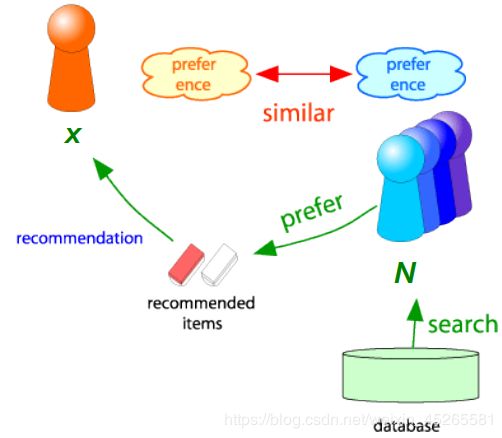
比如这里的用户x是一个新用户,当采集到x的产品偏好数据后,可以根据用户偏好的标签建立模型。根据不同的空间距离算法找到与x行为相似的用户a,b,c,d。通过分析a,b,c,d的偏好并将a,b,c,d也喜欢的评分较高的产品推荐给用户a。
2. 如何找到相似的用户
寻找相似性可分为两个方向,基于产品(item-based)与基于用户(user-based)。值得注意的是我们可以通过简单地改变公式中的变量来改变我们的base。如 r_u,. (user-based) r_.,i (item-based)。在实践中基于产品的(item-based)推荐系统往往有着更好的表现,但为了形象的解释该算法,这里主要介绍基于用户(user-based)的方法,我们通过对数据库中的用户建立坐标系,并在高维坐标系中找到用户之间的关系,也就是用户之间的“距离”。以下几种位置关系在高中时期都有学过,顾不再赘述。
定义变量:
在一个data frame中,有I个用户对J个商品的评价
[ r u 1 , 1 ⋯ r u I , 1 ⋮ r u i , j ⋮ r u 1 , J ⋯ r u I , J ] \begin{bmatrix} r_{u1,1} & \cdots & r_{uI,1}\\ \vdots & r_{ui,j} & \vdots \\ r_{u1,J} & \cdots &r_{uI,J} \end{bmatrix} ⎣⎢⎡ru1,1⋮ru1,J⋯rui,j⋯ruI,1⋮ruI,J⎦⎥⎤
r_u,i : 用户u对产品i的评分(rating)
S_ab:用户a与用户b都有评价的产品
2.1 Jaccard similarity
J S ( A , B ) = ∣ r u a , . ∩ r u b , . ∣ ∣ r u a , . ∪ r u b , . ∣ JS(A,B)=\frac{\left | r_{u_{a},.}\cap r_{u_{b},.}\right |}{\left | r_{u_{a},.}\cup r_{u_{b},.}\right |} JS(A,B)=∣rua,.∪rub,.∣∣rua,.∩rub,.∣
2.2 Cosine similarity
S ( A , B ) = ⟨ r a , . ⋅ r b , . ⟩ ∥ r a , . ∥ ∥ r b , . ∥ S(A,B)=\frac{\left \langle r_{a,.}\cdot r_{b,.}\right \rangle}{\left \|r_{a,.} \right \| \left \| r_{b,.}\right \|} S(A,B)=∥ra,.∥∥rb,.∥⟨ra,.⋅rb,.⟩
2.3 Pearson correlation coefficient
S ( A , B ) = ∑ s ∈ S a b ( r a , s − r a , . ˉ ) ( r b , s − r b , . ˉ ) ∑ s ∈ S a b ( r a , s − r a , . ˉ ) 2 ∑ s ∈ S a b ( r b , s − r b , . ˉ ) 2 S(A,B)=\frac{\sum_{s\in S_{ab}}^{}(r_{a,s}-\bar{r_{a,.}})(r_{b,s}-\bar{r_{b,.}})}{\sqrt{\sum_{s\in S_{ab}}^{}(r_{a,s}-\bar{r_{a,.}})^{2}}\sqrt{\sum_{s\in S_{ab}}^{}(r_{b,s}-\bar{r_{b,.}})^{2}}} S(A,B)=∑s∈Sab(ra,s−ra,.ˉ)2∑s∈Sab(rb,s−rb,.ˉ)2∑s∈Sab(ra,s−ra,.ˉ)(rb,s−rb,.ˉ)
2.4 Euclidean distance
S ( A , B ) = ∑ i ∈ i t e m s ( r a , i − r b , i ) 2 S(A,B)=\sqrt{\sum_{i\in items}^{}(r_{a,i}-r_{b,i})^{2}} S(A,B)=i∈items∑(ra,i−rb,i)2
2.5 Inverse euclidean distance
S ( A , B ) = 1 ∥ r a , . − r b , . ∥ S(A,B)=\frac{1}{\left \| r_{a,.}-r_{b,.}\right \|} S(A,B)=∥ra,.−rb,.∥1
3. 预测用户评分
3.1 User-based system
定义变量:
N:k个用户偏好最接近用户x,且对产品i有打分的用户
预测模型:
∙ 平 均 值 法 h a t r x , i = 1 k ∑ y ∈ N r y , i \bullet 平均值法\quad hat{r_{x,i}}=\frac{1}{k}\sum_{y \in N}^{}r_{y,i} ∙平均值法hatrx,i=k1y∈N∑ry,i
∙ 相 似 度 权 重 法 r x , i ^ = ∑ y ∈ N r y , i ⋅ S i m ( X , Y ) ∑ y ∈ N S i m ( X , Y ) \bullet 相似度权重法\quad \quad \hat{r_{x,i}}=\frac{\sum_{y \in N}^{}r_{y,i}\cdot Sim(X,Y)}{\sum_{y \in N}^{}Sim(X,Y)} ∙相似度权重法rx,i^=∑y∈NSim(X,Y)∑y∈Nry,i⋅Sim(X,Y)
example
假设我们有如下评分表,表示每位用户对每个产品的评分。
我们想要预测用户a对产品2的评分(r_a,2)。满分⭐⭐⭐⭐⭐/5。
| 产品\用户 | a | b | c | d |
|---|---|---|---|---|
| 产品1 | 3 | 2 | 5 | 3 |
| 产品2 | ❓ | 2 | 4 | 2 |
| 产品3 | 2 | 5 | 3 | |
| 产品4 | 5 | 4 | 3 | |
| 产品5 | 1 | 4 | 2 |
solution
goal:找到用户b,c与用户a的相似度 --Pearson correlation
1️⃣首先做row mean的处理
{ r a ˉ = ( 3 + 2 + 5 + 1 ) ÷ 4 = 2.75 r b ˉ = 3.25 r c ˉ = 3.6 r d ˉ = 2.66 \left\{\begin{matrix} \bar{r_{a}}=(3+2+5+1)\div 4=2.75\\ \bar{r_{b}}=3.25 \qquad\qquad\qquad\qquad\quad\;\;\\ \bar{r_{c}}=3.6\qquad\qquad\qquad\qquad\qquad\\ \bar{r_{d}}=2.66\qquad\qquad\qquad\qquad\;\;\;\;\; \end{matrix}\right. ⎩⎪⎪⎨⎪⎪⎧raˉ=(3+2+5+1)÷4=2.75rbˉ=3.25rcˉ=3.6rdˉ=2.66
row mean处理后
| 产品\用户 | a | b | c |
|---|---|---|---|
| 产品1 | 0.25 | -1.25 | 0.34 |
| 产品2 | 0 | -1.25 | -0.66 |
| 产品3 | -0.25 | 1.75 | 0 |
| 产品4 | 2.25 | 0 | 0.34 |
| 产品5 | -1.75 | 0.75 | 0 |
2️⃣找到用户间的相似度
a与b
S ( a , b ) = r a , . ⋅ r b , . ∥ r a , . ∥ ∥ r b , . ∥ = − 2.0625 7.46 = − 0.276 S(a,b)= \frac{r_{a,.}\cdot r_{b,.}}{\left \|r_{a,.} \right \| \left \| r_{b,.}\right \|} =\frac{-2.0625}{7.46}=-0.276 S(a,b)=∥ra,.∥∥rb,.∥ra,.⋅rb,.=7.46−2.0625=−0.276
a与c
S ( a , c ) = 4.2 6.55 = 0.64 S(a,c)=\frac{4.2}{6.55}=0.64 S(a,c)=6.554.2=0.64
a与d
S ( a , d ) = 0.85 2.35 = 0.36 S(a,d)=\frac{0.85}{2.35}=0.36 S(a,d)=2.350.85=0.36
3️⃣预测结果
我们可以看到用户c,d与用户a的行为最接近。所以这里使用k最邻近法,取k=2
k最邻近法原理?为什么取2不取1呢?不熟悉的朋友可以看这一篇:
【算法】如何根据算法在赌场发家致富?汤普森采样之多臂强盗算法!
预测模型
r a , 2 ^ = 0.64 ∗ 4 + 0.36 ∗ 1 0.64 + 0.36 = 2.92 \hat{r_{a,2}}=\frac{0.64*4+0.36*1}{0.64+0.36}=2.92 ra,2^=0.64+0.360.64∗4+0.36∗1=2.92
⭐可以预测出用户a对产品2的评价大约为2.92。
⭐通过平均数法我们可以口算预测出用户a对产品2的评价为3 。
4️⃣小结
i) 基于用户(user-based)的推荐系统对于每一个用户来说,找到与其相似度高的用户很困难。
ii) 在冷启动方面,对于评分很少或者没有评分的新用户很难产生推荐。
iii) 在持续为用户推荐产品的过程中,由于没有足够的数据,很难准确推广新产品。
iv) 推荐结果过于依赖平均值,无法照顾到有独特癖好的用户,并且对用户的品味变换不敏感。
v) 在很多实践中可以发现,基于产品(item-based)的推荐系统往往有着更高的准确率。
4. 总结
本文案例简单介绍了Collaborative Filtering 协同算法的一种简单应用。在上述案例中,我们简单使用了用户对于某一产品的评分作为反馈标准,而在实际的应用中,采集用户对于某一产品的偏好可以通过“点击”,“页面停留时间”,“转发”,“评论”,“购买”,等等 来建立更高维度的坐标系。此外,在推荐系统中往往会使用到多种算法相结合来应对用户的不同时期以及品味的转变。
Reference
Jure Leskovec, Recommender Systems: Content-based System & Collaborative Filtering retrived from http://snap.stanford.edu/class/cs246-2015/slides/07-recsys1.pdf