（七）从零开始学人工智能--搜索:倒排索引

搜索引擎之倒排索引及性能优化

本文主要介绍搜索引擎的一般线上架构，并详细介绍引擎核心的基础结构之倒排索引的实现原理，倒排性能优化相关的算法和数据结构，最后会提出搜索引擎所面对的一些最新的技术挑战。

1. 搜索引擎的一般线上架构

当我们在类似百度/谷歌的搜索引擎中输入一个query，后台服务器到底发生了什么呢？请看下图为搜索引擎的一般线上架构。

图1-1 搜索引擎线上架构

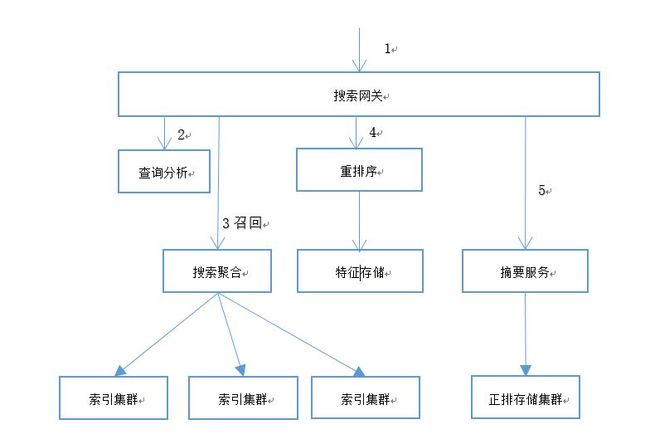
简单来说，后台包括了如下的主要步骤：

• 用户输入一个query，前端把query传给搜索网关；

• 接下来需要查询分析服务先对query进行查询语义的分析，可能会调用分词，query的分类，query的意图识别等服务，最终生成query的查询计划，这个步骤你可以理解为mysql里面的sql解析和查询计划和策略的生成；

• 然后下发请求到索引集群进行搜索结果的召回，通常是每个节点几十条结果，这样在顶层节点聚合后可以有几千条结果；召回的过程会进行第一次粗略的排序；

• 然后调用重排序服务，对召回结果进行多次，多种策略的重新排序；

• 最后从摘要服务获取需要展示的信息如摘要，标题，作者等。

这里只是一个简化的线上搜索系统架构，省略了离线部分的架构，同时真正的系统可能还会有对query进行纠错，联想，推荐，广告等等服务，索引，存储等集群的详细结构也在此略过。后续章节我们主要集中在第三步，即如何从百亿千亿的文档中找到用户需要的文档子集。

2. 倒排索引(Inverted Index)及性能优化

在搜索引擎中有正向索引（forward index），自然也有倒排索引（inverted index）。想象一下一个类似淘宝的电商网站的搜索引擎，其正向索引存储的就是每个商品及其对应的一大堆属性，索引是以商品id为key，其它属性为值，比如标题，图片，价格等等。而倒排索引正好反过来，索引是以文本中的单词（或者其他属性值比如价格）为key，value为商品的id列表。另一个倒排索引常见的例子是书的附录页中的索引，即专有名词或图片到页数的索引。

2.1 词的经验分布zipf’s law

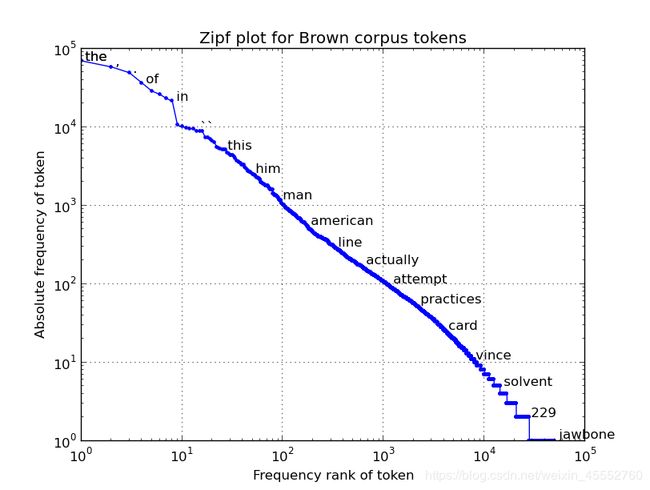
在正式介绍倒排索引前，我们有必要了解下词在我们常见文章中的分布，即zipf’s law。齐夫定律（英语：Zipf’s law）是由哈佛大学的语言学家乔治·金斯利·齐夫（George Kingsley Zipf）于1949年发表的实验定律。它可以表述为：在自然语言的语料库里，一个单词出现的频率与它在频率表里的排名成反比。所以，频率最高的单词出现的频率大约是出现频率第二位的单词的2倍，而出现频率第二位的单词则是出现频率第四位的单词的2倍。这个定律被作为任何与幂定律概率分布有关的事物的参考。

最简单的齐夫定律的例子是“1/f function”。给出一组齐夫分布的频率，按照从最常见到非常见排列，第二常见的频率是最常见频率的出现次数的½，第三常见的频率是最常见的频率的1/3，第n常见的频率是最常见频率出现次数的1/n。然而，这并不精确，因为所有的项必须出现一个整数次数，一个单词不可能出现2.5次。

齐夫定律是一个实验定律，而非理论定律，可以在很多非语言学排名中被观察到，例如不同国家中城市的数量、公司的规模、收入排名等。但它的起因是一个争论的焦点。齐夫定律很容易用点阵图观察，坐标分别为排名和频率的自然对数（log）。比如，“the”用上述表述可以描述为x = log(1), y = log（69971）的点。如果所有的点接近一条直线，那么它就遵循齐夫定律。

在Brown语料库中，“the”、“of”、“and”是出现频率最前的三个单词，其出现的频数分别为69971次、36411次、28852次，大约占整个语料库100万个单词中的7%、3.6%、2.9%，其比例约为6：3：2。大约占整个语料库的7%（100万单词中出现69971次）。满足齐夫定律中的描述。仅仅前135个字汇就占了Brown语料库的一半。

图2-1 brown语料库词频和词排名关系

2.2 倒排的一些基本概念

倒排索引里面有如下的一些基本概念，

• 文档(Document)：一般搜索引擎的处理对象是互联网网页，而文档这个概念要更宽泛些，代表以文本形式存在的存储对象，相比网页来说，涵盖更多种形式，比如Word，PDF，html，XML等不同格式的文件都可以称之为文档。再比如一封邮件，一条短信，一条微博也可以称之为文档。在本书后续内容，很多情况下会使用文档来表征文本信息。
• 文档集合(Document Collection)：由若干文档构成的集合称之为文档集合。比如海量的互联网网页或者说大量的电子邮件都是文档集合的具体例子。
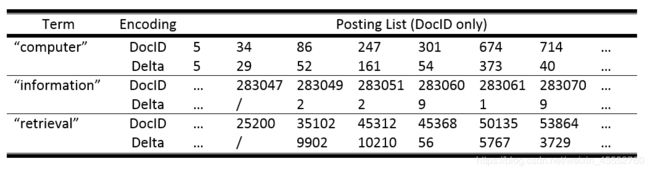
• 文档编号(Document ID)：在搜索引擎内部，会将文档集合内每个文档赋予一个唯一的内部编号，以此编号来作为这个文档的唯一标识，这样方便内部处理，每个文档的内部编号即称之为“文档编号”，后文有时会DocID来便捷地代表文档编号。
• 单词编号(Word ID)：与文档编号类似，搜索引擎内部以唯一的编号来表征某个单词，单词编号可以作为某个单词的唯一表征。
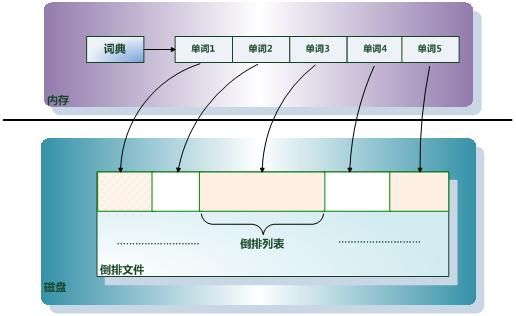
• 倒排索引(Inverted Index)：倒排索引是实现“单词-文档矩阵”的一种具体存储形式，通过倒排索引，可以根据单词快速获取包含这个单词的文档列表。倒排索引主要由两个部分组成：“单词词典”和“倒排文件”。
• 单词词典(Lexicon)：搜索引擎的通常索引单位是单词，单词词典是由文档集合中出现过的所有单词构成的字符串集合，单词词典内每条索引项记载单词本身的一些信息以及指向“倒排列表”的指针。词典常用的数据结构有Hash table, B-tree, trie树等。
• 倒排列表(PostingList)：倒排列表记载了出现过某个单词的所有文档的文档列表及单词在该文档中出现的位置信息，每条记录称为一个倒排项(Posting)。根据倒排列表，即可获知哪些文档包含某个单词。
• 倒排文件(Inverted File)：所有单词的倒排列表往往顺序地存储在磁盘的某个文件里，这个文件即被称之为倒排文件，倒排文件是存储倒排索引的物理文件。

关于这些概念之间的关系，通过下图可以比较清晰的看出来。

图2-2 词典倒排关系

2.2.1 常用词典数据结构

很多数据结构均能完成词典功能，总结如下。

数据结构	优缺点
排序列表Array/List	使用二分法查找，不平衡
HashMap/TreeMap	性能高，内存消耗大，几乎是原始数据的三倍
Skip List	跳跃表，可快速查找词语，在lucene、leveldb、redis、Hbase等均有实现。相对于TreeMap等结构，特别适合高并发场景
Trie	适合英文词典，如果系统中存在大量字符串且这些字符串基本没有公共前缀，则相应的trie树将非常消耗内存
Double Array Trie	适合做中文词典，内存占用小，很多分词工具均采用此种算法
Ternary Search Tree	三叉树，每一个node有3个节点，兼具省空间和查询快的优点
Finite State Transducers (FST)	类似trie树的一种有限状态转移机，Lucene 4有开源实现，并大量使用。具体可参考lucene-fst

2.3 倒排索引简单实例

倒排索引从逻辑结构和基本思路上来讲非常简单。下面我们通过具体实例来进行说明，让大家能够对倒排索引有一个宏观而直接的感受。

假设文档集合包含五个文档，每个文档内容如下图所示，在图中最左端一栏是每个文档对应的文档编号。我们的任务就是对这个文档集合建立倒排索引。

图2-3 文档集合示例

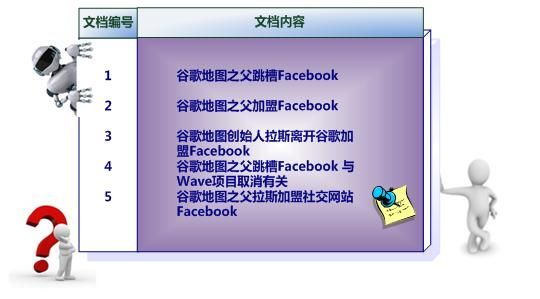
中文和英文等语言不同，单词之间没有明确分隔符号，所以首先要用分词系统将文档自动切分成单词序列。这样每个文档就转换为由单词序列构成的数据流，为了系统后续处理方便，需要对每个不同的单词赋予唯一的单词编号，同时记录下哪些文档包含这个单词，在如此处理结束后，我们可以得到最简单的倒排索引（参考图2-4）。在图2-4中，“单词ID”一栏记录了每个单词的单词编号，第二栏是对应的单词，第三栏即每个单词对应的倒排列表。比如单词“谷歌”，其单词编号为1，倒排列表为{1,2,3,4,5}，说明文档集合中每个文档都包含了这个单词。

图2-4 简单倒排索引例子

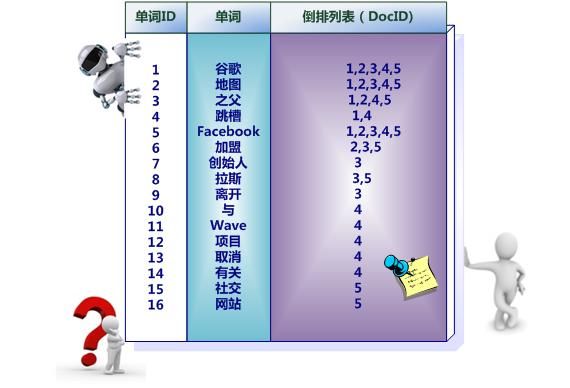
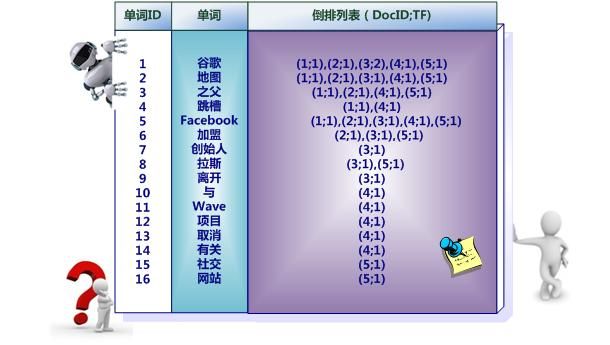
图2-4所示倒排索引是最简单的，是因为这个索引系统只记载了哪些文档包含某个单词，而事实上，索引系统还可以记录除此之外的更多信息。图2-5是一个相对复杂些的倒排索引，与图2-4的基本索引系统比，在单词对应的倒排列表中不仅记录了文档编号，还记载了单词频率信息（TF），即这个单词在某个文档中的出现次数，之所以要记录这个信息，是因为词频信息在搜索结果排序时，计算查询和文档相似度是很重要的一个计算因子，所以将其记录在倒排列表中，以方便后续排序时进行分值计算。在图2-5的例子里，单词“创始人”的单词编号为7，对应的倒排列表内容为：（3:1），其中的3代表文档编号为3的文档包含这个单词，数字1代表词频信息，即这个单词在3号文档中只出现过1次，其它单词对应的倒排列表所代表含义与此相同。

图2-5 包含词频的倒排索引例子

2.4 从倒排到搜索

我们用简单的一个布尔查询的模型来描述一下，如何从倒排索引最终返回结果。所谓布尔查询，就是以AND，OR，NOT，MUST等操作符将词项连接起来的查询。假如我们已经构建好了如图2-5的倒排索引，查询条件为谷歌 AND 地图 AND 跳槽，首先我们从词典获取谷歌，地图，跳槽三个term对应的倒排列表，由于是AND的关系，然后对这三个倒排进行归并求交集。可以看出第一个文档1是符合条件的，第二个文档从跳槽这个term的倒排列表看是文档4，由于是AND，那么其它几个term的倒排列表也要往后遍历找文档4是否在里面，显然在谷歌和地图的倒排列表里面有这个文档。然后再下一个，跳槽这个term已经没有新文档了，查询结束。

实际的搜索与上述过程步骤上差不多，不同的是，由于文档数量众多，我们会需要一个类似heap的结构来保存TopN，会需要一个打分公式来对每篇文档进行粗排的打分，在输入词较少的情况下，一般会用OR的模型来召回。

2.4 搜索的性能优化

那么搜索引擎如何在几百毫秒级完成对百亿甚至千亿级别的文档的快速检索呢？下面我们来介绍几种常见的策略和算法。

2.4.1跳跃表结构

跳跃表实际上是一种以空间换时间的算法，主要实现在倒排索引层。

SkipList在leveldb以及各搜索引擎中都广为使用，是比较高效的数据结构。由于它的代码以及原理实现的简单性，更为人们所接受。我们首先看看SkipList的定义，为什么叫跳跃表？

“ Skip lists are data structures that use probabilistic balancing rather than strictly enforced balancing. As a result, the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees. ”

译文：跳跃表使用概率均衡技术而不是使用强制性均衡，因此，对于插入和删除结点比传统上的平衡树算法更为简洁高效。 

我们看一个图就能明白，什么是跳跃表，如图所示：

图2-6 跳跃表

如图2-6所示，是一个即为简单的跳跃表。传统意义的单链表是一个线性结构，向有序的链表中插入一个节点需要O(n)的时间，查找操作需要O(n)的时间。如果我们使用图1所示的跳跃表，就可以减少查找所需时间为O(n/2)，因为我们可以先通过每个节点的最上面的指针先进行查找，这样子就能跳过一半的节点。比如我们想查找19，首先和6比较，大于6之后，在和9进行比较，然后在和12进行比较…最后比较到21的时候，发现21大于19，说明查找的点在17和21之间，从这个过程中，我们可以看出，查找的时候跳过了3、7、12等点，因此查找的复杂度为O(n/2)。查找的过程如下图：

图2-7 跳跃表查询过程

其实，上面基本上就是跳跃表的思想，每一个结点不单单只包含指向下一个结点的指针，可能包含很多个指向后续结点的指针，这样就可以跳过一些不必要的结点，从而加快查找、删除等操作。对于一个链表内每一个结点包含多少个指向后续元素的指针，这个过程是通过一个随机函数生成器得到，这样子就构成了一个跳跃表。这就是为什么论文“Skip Lists : A Probabilistic Alternative to Balanced Trees ”中有“概率”的原因了，就是通过随机生成一个结点中指向后续结点的指针数目。随机生成的跳跃表可能如下图所示：

​

图2-8 随机跳跃表

2.4.2 分布式索引和备份请求

我们先来估算一下索引对存储的需求，假设：

• 网页数：1000亿，假设 50％ 是 text 文本
• 平均网页大小：40K
• 假设 non-text 网页的平均入链数：1K
• 索引大小约为原始文本大小的 40％

Text: 50billion *40K + 50billion *1K = 2050TB
Index: 40% * 2050TB = 820TB

​对于820TB大数据量的倒排索引，我们很自然的想到可以用分布式来解决，正所谓没有什么工程性能问题是不能通过钱来解决的。如下图的树形结构就是一般大型搜索引擎系统采用的获取第一级候选集的基础结构：

​ 图2-9 索引集群分层结构

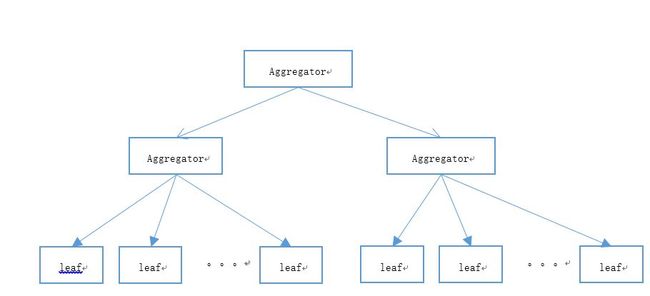
Aggregator为聚合器，将请求往下层节点分发，leaf节点为基础的搜索节点，数据分片再加多实例备份，即解决性能问题，也解决一部分的吞吐量。具体采用几层，采用多少类似数据集群看应用而定，一般来说，大型搜索引擎对数据会进行一定的分层：比如根据重要性区分为top重要VS一般重要VS不重要的站点，实时更新的数据可能也会有单独的集群，还有视频，图片等的角度划分。

在分布式索引上谷歌等公司还使用了一项技术——备份请求（Backup Requests），大致的思路是先把请求发给一个副本，请求会被放进队列；随后再给另一个副本发送相同请求，如果第二个副本处理地很快，处理完毕后发回结果，客户端再给第一个副本发送取消任务请求，这样能在牺牲一部分资源的情况下提高响应时间。这项技术对于上百个服务的搜索引擎，对降低中长尾请求的响应时间起到非常重要的效果。

Jeff dean提供了一个例子，在分布式文件系统客户端中发送读请求，等待 2 毫秒后发送备份请求，耗时情况如下：

• 集群处于空闲状态

  • 没有备份请求，50%ile 为 19 毫秒，90%ile 为 38 毫秒，99%ile 为 67 毫秒，99.9%ile 为 98 毫秒
  • 有备份请求，50%ile 为 16 毫秒，90%ile 为 28 毫秒，99%ile 为 38 毫秒，99.9%ile 为 51 毫秒

• 集群正在进行大量排序

  • 没有备份请求，50%ile 为 24 毫秒，90%ile 为 56 毫秒，99%ile 为 108 毫秒，99.9%ile 为 159 毫秒

  • 有备份请求，50%ile 为 19 毫秒，90%ile 为 35 毫秒，99%ile 为 67 毫秒，99.9%ile 为 108 毫秒

两种情况下，使用备份请求延时都有显著改善，99%ile 分别下降了 43% 和 38%，在第二种情况下备份请求只引入了大约 1% 的额外磁盘读请求。如果没有备份请求，集群需要一直处于低负载状态，而使用了备份请求，集群则可处于相对较高的负载，同时还能有相对较好的响应延时。备份请求也不是万能的，对于一些不可重复执行得请求，比如在线交易，就不能使用备份请求，以免造成数据不一致等情况。

2.4.3 索引压缩

由于倒排索引文件往往占用巨大的磁盘空间，我们自然想到对数据进行压缩。同时，引进压缩算法后，使得磁盘占用减少，操作系统在query processing过程中磁盘读取效率也能提升。另外，压缩算法不仅要考虑压缩效果，还要照顾到query processing过程的解压缩效率。

总的来说，好的索引压缩算法需要最大化两个方面：

​ 1、减少磁盘资源占用

​ 2、加快用户查询响应速度

其中，加快响应速度比减少磁盘占用更为重要。下面以PForDelta压缩算法为例作简单介绍。

一个posting单元由组成。对于每个DocID，其保存在硬盘中的大小取决于文件集最大文档编号的大小。这样造成编号较小的DocID分配了和编号较大的DocID（上百万）一样的存储空间，浪费了资源。由于每个posting是根据DocID顺序存储，所以不需要保存DocID，只需要保存前后两个DocID的差值，这样可以大大减小DocID储存空间，这种方式成为Delta Encoding。如下图：

图2-10 索引delta编码

对于tf值，根据Zipf定律，tf值较小的term占大多数，我们可以对这类tf值少分配一些空间保存。而tf大的term占少数，对这些tf分配多空间储存。基于上述排列特性，往往将docID和tf及其他数据分开放置，方便数据压缩。最终，整体的存储结构如下图所示：

图2-11 索引block

为了方便分布式存储倒排索引文件，Data Block是硬盘中的基础存储单元。由于建立过程需要，每个term 的postinglist被拆分为多个部分保存在多个block中（如图不同颜色的block代表存储不同term的postinglist）。也就是说，每个block内部可能包含多个term的postinglist片段。

Data block的基本组成单元是数据块（chunk），每个chunk一般包含固定数量的posting，图中所示一个chunk包含128个posting，这些posting都属于同一个term。其中将DocID、tf和position分开排放，方便压缩。

这样以block为单元，以chunk为基础元素的索引存储的方式，一方面可以支持使用caching的方法缓存最常用term的postinglist，提高query响应速度。另一方面，所有压缩解压缩过程都以chunk为单位，都在chunk内部进行。当需要查找某一term的postinglist时，不需要对所有文件进行解压缩。对于不相关的chunk直接忽略，只需要对少部分block中的目标chunk进行处理，这样又从另一个方面大大缩短了query响应时间。这也是chunk机制设置的初衷。接下来，我们讨论如何对一个chunk结构进行压缩和解压缩处理。

PForDelta算法

PForDelta算法最早由Heman在2005年提出（Heman et al ICDE 2006），它允许同时对整个chunk数据（例128个数）进行压缩处理。基础思想是对于一个chunk的数列（例128个），认为其中占多数的x%数据（例90%）占用较小空间，而剩余的少数1-x%（例10%）才是导致数字存储空间过大的异常值。因此，对x%的小数据统一使用较少的b个bit存储，剩下的1-x%数据单独存储。

举个例子，假设我们有一串数列23, 41, 8, 12, 30, 68, 18, 45, 21, 9, …。取b = 5，即认为5个bit（32）能存储数列中大部分数字，剩下的超过32的数字单独处理。从可见的队列中，超过32的数字有41, 68, 45。那么PForDelta压缩后的数据如下图所示（图中将超过32的数字称为异常值exception）：

图2-12 PForDelta算法示例

图中第一个单元（5bit）记录第一个异常值的位置，其值为“1”表示间隔1个b-bit之后是第一个异常值。第一个异常值出现在“23”之后，是“41”，其储存的位置在队列的最末端，而其在128个5bit数字中的值“3”表示间隔3个b-bit之后，是下一个异常值，即“68”，之后依次类推。异常值用32bit记录，在队列末尾从后向前排列。

上述队列就对应一个chunk（DocID），还需要另外记录b的取值和一个chunk压缩后的长度。这样就完整的对一个chunk数据进行了压缩。

但是这样算法有一个明显的不足：如果两个异常值的间隔非常大（例如超过32），我们需要加入更多的空间来记录间隔，并且还需要更多的参数来记录多出多少空间。为了避免这样的问题，出现了改进的算法NewPFD。

改进的PForDelta算法

在PForDelta算法基础上，H. Yan et.al WWW2009提出NewPFD算法及 OptPFD算法。

NewPFD算法

由于PForDelta算法最大的问题是如果异常值间隔太大会造成b-bit放不下。NewPFD的思路是：128个数最多需要7个bit就能保存，如果能将第二部分中保存异常值的32bit进行压缩，省出7bit的空间用于保存这个异常值的位置，问题就迎刃而解了。同时更自然想到，如果异常值位置信息保存在队列后方的32bit中，那么队列第一部分原用于记录异常值间隔的对应部分空间就空余出来了，可以利用这部分做进一步改进。

因此，NewPFD的算法是，假设128个数中，取b=5bit，即32作为阈值。数列中低于32的数字正常存放，数列中大于32的数字，例如41 (101001) 将其低5位（b-bit）放在第一部分，将其剩下的高位（overflow）存放在队列末端。我们依然以PForDelta中的例子作为说明，一个128位数列23, 41, 8, 12, 30, 68, 18, 45, 21, 9, …。经过NewPFD算法压缩后的形式如下图所示：

图2-13 NewPFD算法示例

NewPFD算法压缩后的数据依然包括两部分，第一部分128个b-bit数列，省去了第一个异常值位置单元；第二部分异常值部分包含异常值的位置和异常值的高位数字。例如，对于异常值“41”其2进制码为101001，那么低5位01001保存在数据块第一部分。在第二部分中，先保存位置信息（“41”的位置是“1”，表示原数列第2个），再以字节为单位保存高位“1”即“0000 0001”，这样反而只需要附加2个字节（一个保存位置，一个保存高位）就可以储存原本需要4个字节保存的异常值。而对于高位字节，还可以继续使用压缩算法进行压缩，本文不再继续讨论。

除了数据列，NewPFD算法还需要另外保存b值和高位占的字节数（称为a值）。因为参数ab已经确定了数据块的长度，因此chunk长度值不用再单独记录。

OptPFD算法

OptPFD算法在NewPFD之上，认为每个数据压缩单元chunk应该有适应自己数据的独立a值和b值，这样虽然需要保存大量的ab值，但是毕竟数据量小不会影响太大的速度，相反，由于对不同chunk单独压缩，使压缩效果更好，反而提高了解压缩的效果。

对于b的选取，通常选择2^b可以覆盖数列中90%的数字，也就是控制异常值在10%左右，这样可以获得压缩效果和解压缩效率的最大化。

2.4.4 提前结束early termination

提前结束(early termination)顾名思义就是在已经有足够好结果的情况下提前结束搜索过程。举个例子，假设我们要遍历出前N个文档，并且文档是按 date 字段排序的。如果索引存储在磁盘上时已经是有序的了，那么我们遍历出前N个文档就可以直接返回，而不需要遍历所有的文档。这就是我们所说的“early termination”。提早的返回查询结果，可以明显的缩短查询响应时间，特别是含有排序的查询。

这个策略有几种场景：

• 本身索引中的doc id是按照某个字段预先严格排序好的，比如发布时间，比如商品综合质量等，但一般来说索引只支持按某个字段的预排序。
• 本身索引是按质量分层的，比如优质商品集合，次优质，一般商品等等，那么我们可以先在优质商品集合上检索，如果结果不够，再在次优质商品集合上搜索。
• 本身索引不是严格有序，但是概率上有序，比如前面一段文档的质量比后一段的文档质量高。那么也是可以实施这个策略的。

目前开源的引擎如elastic search是支持按照某个字段预先排序，然后可以支持提前结束策略的。

2.4.5 缓存

缓存是任何系统提高性能的必要手段，对于搜索引擎尤其如此。用户在使用搜索引擎进行检索时，查询词可能千差万别。但是如果从大量用户的查询统计上看，总会有一些词汇经常被查询，有些词汇却很少被查询。用户发出的查询请求分布也符合zipf‘s law规则，即少数查询占了查询总数的相当比例，而大多数查询出现次数非常少。在十亿规模的搜索日志记录中，60%+的用户查询只出现过一次。

对于搜索引擎缓存，在存储区内存放的数据对象并不是唯一的，可以是搜索结果，也可以是某个查询词汇对应的倒排列表，或者是一些搜索的中间结果。最常见的缓存对象类型是用户查询请求所对应的搜索结果。

3.搜索引擎未来的一些挑战

虽然搜索引擎已经是一项发展了20多年的技术，在索引和索引压缩等各个方面已经非常成熟，但目前还是面临几方面的挑战：

• 个性化，用户很多时候并不确切地知道自己想要什么样的结果，除非你把结果放在他的面前。所以用户在使用搜索引擎时，很多时候相同表象的内容却意味着不同的需要。比如对于同一个查询词，不同的用户所需要的查询结果可能是不同的。即使是同一个用户输入同一个查询词，他在不同的时间、不同的地点和不同的查询背景下，希望得到的查询结果也可能是不一样的。

• 直接答案。Larry Page 曾经说过，“最终的搜索引擎应该能理解世界上的所有事情，并总是告诉你正确的答

  案。”在 Google 看来，目前的搜索引擎在理解语义上还在初级阶段，离完美还很遥远。

• 多模态搜索。随着宽带技术的发展，未来的互联网是多媒体数据的时代。开发出支持文本、声音、图片和视频的多媒体搜索引擎是一个新的方向。

  ​

声明

本博客所有内容仅供学习，不为商用，如有侵权，请联系博主谢谢。

参考文献

[1] 什么是倒排索引
[2] 倒排索引压缩：改进的PForDelta算法
[3] Jeff Dean 谈如何在大型在线服务中做到快速响应
[4] Search Engines笔记 - Index Construction
[5] Achieving Rapid Response Times in Large Online Services