最大堆最小堆操作——python
刚讲完堆的一系列基本内容,把涉及的知识点整理下,看课本81-88页自行对照复习。
- 堆heap,通常是一个可以被看做一棵树的数组对象。
- 堆的性质:(1)是轶可完全二叉树;(2)某个节点的值总是大于或小于子节点
- 相关的操作有用VB或C++实现的,其它的请自行百度,我们采用python完成
- 算法开始,已知条件:序列A = [45, 36, 18, 53, 72, 30, 48, 93, 15, 35],如下图所示,利用我们课本上的算法buildHeap如何将序列A转化为一个堆呢?

- 注意构造的时候,从堆树的叶子节点开始,按照自底向上逐层处理每个节点,保证节点的堆化过程不重复。叶子节点不用说,符合条件不用处理,那就从第一个有叶子的分支节点开始处理,也就是mid=len(A)//2,观察上图可知mid=10//2=5,也即是索引为5的节点开始处理,正好是第一个有叶子的节点72,其它的类似这类节点有53,18,36,45都要检查是否满足最大堆特性,不满足就拉下马,降低它的级别,直到堆根节点进行调整后,整个树就变成了一个堆。教材上初始化堆的时候加了个0,是模仿Python的heapq库函数来设计的,就是为了比较节点索引使用的。
The initial seq is [0, 45, 36, 18, 53, 72, 30, 48, 93, 15, 35]:
- 检查72这个节点的左孩子的大小,也就是通过maxChild来找72这个节点最大的孩子节点,没找到35<72,所以72不变,mid递减=4,看下图:

- 接下来找mid=4,也即53这个节点,发现左孩子93>53,则53下沉,两个互换下位置,这里要注意53拉下马之后,53的索引变成了8,这个时候仍然要递归索引8到最大堆化函数中检查是否满足最大堆条件,什么时候停止呢?假设索引为i,则判断下2*i是否小于等于序列长度即可。见下图:
4-th -> 8-th node, seq is:[0, 45, 36, 18, 93, 72, 30, 48, 53, 15, 35]
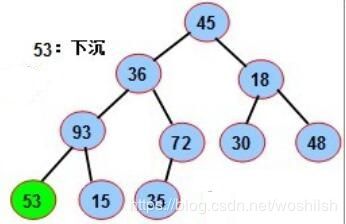
8. 上面检查发现53符合要求,不用动了。继续创建堆,这个时候mid=3,也就是要看节点18了,找最大孩子节点48,索引i=7,没办法了,交换吧,代码输出和结果示意图如下:
3-th -> 7-th node, seq is:[0, 45, 36, 48, 93, 72, 30, 18, 53, 15, 35]
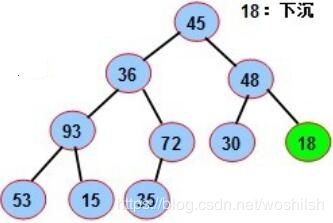
9. 交换后18的索引成了7,对7继续递归调用最大化堆化操作,检查满足结束条件,mid继续减少,mid=2,对索引为2,节点为36的点调用最大化堆化操作,不重复了,最大的孩子节点为93,索引i=4,没办法,交换位置:
2-th -> 4-th node, seq is:[0, 45, 93, 48, 36, 72, 30, 18, 53, 15, 35]

对36节点的索引4继续调用最大堆堆化操作,发现最大孩子是节点53,索引为8,没办法,互换:
4-th -> 8-th node, seq is:[0, 45, 93, 48, 53, 72, 30, 18, 36, 15, 35]
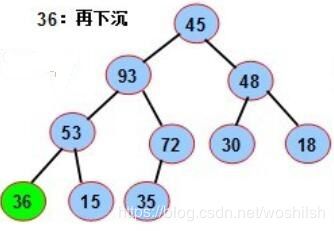
36拉下来之后,继续迭代调用最大化堆化函数,满足结束条件
10. mid=1,调用最大堆堆化函数,最大的孩子节点是93,索引为2,互换:
1-th -> 2-th node, seq is:[0, 93, 45, 48, 53, 72, 30, 18, 36, 15, 35]
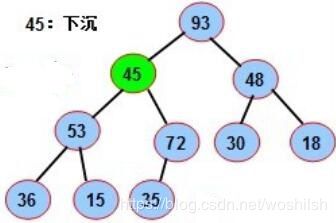
对45,索引为2的继续迭代调用最大化堆化,发现最大的孩子节点是72,索引为5,没办法了,继续互换:
2-th -> 5-th node, seq is:[0, 93, 72, 48, 53, 45, 30, 18, 36, 15, 35]

11. 按照上述执行完之后打印结果,如下:

12. 构建堆思路继续整理下:
(1)找要开始处理的点的索引,参考数组存放堆的数学公式,节点i的父节点索引(i/2),左子节点索引(2i),右子节点索引(2i+1)。而且我们已知对于节点数为n的完全二叉树,叶子节点数n0=n/2,所以要找第一个有叶子的节点的索引很简单:n为偶数,n/2;n为奇数,(n+1)/2。这个值求出来后赋给mid。
(2)对当前的mid对应的节点执行最大堆堆化操作,然后mid递减,直到mid>0时停止,这步就能完成构建堆的任务。
13. 最大堆化思路继续整理下:
(1)传入的索引,要检查下是否存在子节点,也就是检查下(2i)是否小于序列长度。还是使用上面的数学公式设计这个边界条件。满足则执行下面的其它操作,否则直接返回。
(2)找当前索引i的最大的子节点的索引mc,这里找到的还是索引,所有的操作均再索引上进行。
(3)比较当前索引i和索引mc对应的节点值的大小,如果当前找到比i对应节点还大,则交换位置,同时递归调用最大堆化操作
14. 最大子节点思路继续整理:
(1)输入当前索引i,找到左孩子索引(2i),右孩子索引(2i+1).
(2)如果左孩子大于当前节点,则最大值等于左孩子,否则还是当前节点最大。
(3)如果右孩子大于最大节点,则最大值等于右孩子。
(4)最后返回当前节点索引下找到的最大值对应节点的索引
15. 好,算法整体完成,思路啰嗦点,但是递归看起来很清晰,时间复杂度么:构造——O(n),最大堆化——O(logn),完整算法代码如下,里面包含了打印功能:
#coding=utf-8
from __future__ import print_function
import math, random
import heapq
class BinHeap:
def __init__(self):
self.heapList = [0]
self.currentSize = 0
def max_heapify_rec(self, i):
if (i * 2) <= self.currentSize:
mc = self.maxChild(i)
if self.heapList[i] < self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
print("%d-th -> %d-th node, seq is:%s" % (i, mc, self.heapList))
self.max_heapify_rec(mc)
def maxChild(self, i):
leftchild = i * 2
rightchild = i * 2 + 1
if leftchild <= self.currentSize and self.heapList[leftchild] > self.heapList[i]:
largest = leftchild
else:
largest = i
if rightchild <= self.currentSize and self.heapList[rightchild] > self.heapList[largest]:
largest = rightchild
return largest
def max_heapify(self, i):
while (i * 2) <= self.currentSize:
mc = self.maxChild[i]
if self.heapList[i] < self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
i = mc
def buildHeap(self, alist):
mid = len(alist) // 2
self.currentSize = len(alist)
self.heapList = [0] + alist[:]
print("The initial seq is %s:" % self.heapList)
while (mid > 0):
self.max_heapify_rec(mid)
mid = mid - 1
return self
def heapsort(alist):
sortedh = []
heapify(alist)
while alist:
sortedh.append(heappop(alist))
return sortedh
def print_tree(array):
index = 1
depth = math.ceil(math.log(len(array), 2))
sep = ' '
for i in range(int(depth)):
offset = 2 ** i
print(sep * (2 ** (int(depth) - i - 1) - 1), end = ' ')
line = array[index:index+offset]
for j, x in enumerate(line):
print("{:>{}}".format(x, len(sep)), end = ' ')
interval = 0 if i == 0 else 2 ** (int(depth) - i) - 1
if j < len(line) - 1:
print(sep * interval, end = ' ')
index += offset
print()
- 调用上述代码:
A = [45, 36, 18, 53, 72, 30, 48, 93, 15, 35]
bh = BinHeap()
bh.buildHeap(A)
print_tree(bh.heapList)
- 好了对照下标准库,大部分库函数的操作都是O(n)的时间复杂度,里面有个函数heapify(x),将列表x转化为一个堆,时间复杂度时O(len(x)),其实我们实现的buildheap函数也是实现了这个功能,当然时间复杂度是一样的。
- 标准库的_siftup_max函数和我们实现的max_heapify_rec类似,就是将更大的孩子用冒泡的思路移动起来。
- 其它的还有一些好用的函数可以琢磨使用下,就不多说了,大家自己挖掘去吧。