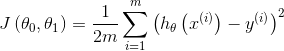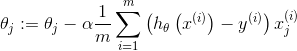机器学习基础__03__梯度下降法

目录

1. 什么是梯度

1.1 方向导数

1.2 梯度

1.3  为什么沿着梯度方向函数增长最快

2. 梯度下降法

3. 梯度下降法的三种形式

3.1 批量梯度下降

3.2 随机梯度下降

3.3 小批量梯度下降

---

1. 什么是梯度

梯度是一个向量。（有大小有方向）

1.1 方向导数

导数
导数表示切线的斜率，公式如下：
                               
 

导数的物理意义表示函数在这一点的 (瞬时) 变化率。

 

偏导数
导数是针对单个自变量，考虑的是曲线上的切线，曲线上某个点的切线只有一条。
偏导数是针对多个自变量，考虑的是曲面上的，曲面上某个点的切线有无数条。

因为曲面上的每一点都有无穷多条切线，描述这种函数的导数相当困难。偏导数就是选择其中一条切线，并求出它的斜率。通常，最感兴趣的是垂直于 y 轴（平行于 xOz 平面）的切线，以及垂直于 x 轴（平行于 yOz 平面）的切线。
                                          
 

偏导数的物理意义表示函数沿着坐标轴正方向上的变化率。

方向导数
偏导数研究的是指定方向 (坐标轴方向) 的变化率，而方向导数是研究任意方向的变化率。
方向导数的物理意义表示函数在某点沿着某一特定方向上的变化率。

1.2 梯度

某个函数的方向导数有很多，最大的那个就是梯度。
函数在某点的梯度是一个向量，它的方向就是方向导数最大值的那个方向。
梯度方向函数值增加最快，梯度负方向函数值减小最快。

梯度公式
设二元函数在点处具有一阶偏导数，则定义
                            
为在点处的梯度。

1.3  为什么沿着梯度方向函数增长最快

参考：http://liuchengxu.org/blog-cn/posts/dive-into-gradient-decent/

一句话总结：
导数：函数在该点的瞬时变化率
偏导数：函数在坐标轴方向上的变化率
方向导数：函数在某点沿某个特定方向的变化率
梯度：函数在该点沿所有方向变化率最大的那个方向 

2. 梯度下降法

参考1：https://blog.csdn.net/wwyl1001/article/details/78571672
参考2：https://blog.csdn.net/wwyl1001/article/details/78944968

3. 梯度下降法的三种形式

一句话总结：
批量梯度下降：每次迭代使用全部样本对参数进行更新
随机梯度下降：每次迭代使用随机一个样本对参数进行更新
小批量梯度下降：每次迭代使用batch_size个样本对参数进行更新，它是最常用的。

梯度下降法作为机器学习中较常使用的优化算法，其有着三种不同的形式：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。
其中，小批量梯度下降在机器学习/深度学习中最常用。

为了便于理解，这里我们将使用只含有一个特征的线性回归来展开。此时线性回归的假设函数为：
                                             ，其中i = 1, 2, ..., m表示样本数

回归问题的代码函数为均方误差：
                                            
代码函数图像是：
                                         

梯度下降法一般形式:
repeat {
      
}                             

3.1 批量梯度下降

批量梯度下降是在做每次迭代参数更新时，取全部所有样本。

对目标函数求偏导：
                                 
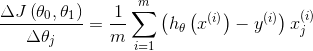
其中i = 1, 2, ..., m表示样本数，j =0, 1表示特征数，设。

因此，批量梯度下降形式为：
repeat {
       
}

注意：这里有个求和函数，m是所有样本。

优点：由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优
缺点：当样本数目 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢，另外内存也吃不消。

3.2 随机梯度下降

随机梯度下降法不同于批量梯度下降，随机梯度下降是每次迭代随机使用一个样本来对参数进行更新。使得训练速度加快。

一个样本的目标函数是：
                          

对目标函数求偏导：
                          

因此，随机梯度下降形式：
repeat {
         for i = 1,..., m {
                   
         }
}

注意，这里不再有求和了，每次参数更新只有一个样本。

为什么SGD比BGD收敛快？
这里我们假设有30W个样本，对于BGD而言，每次迭代需要计算30W个样本才能对参数进行一次更新，需要求得最小值可能需要多次迭代（假设这里是10）；而对于SGD，每次更新参数只需要一个样本，因此若使用这30W个样本进行参数更新，则参数会被更新（迭代）30W次（SGD参数更新迭代次数多），而这期间，SGD就能保证能够收敛到一个合适的最小值上了。

3.3 小批量梯度下降

小批量梯度下降，是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代使用batch_size个样本来对参数进行更新。它是最常用的。

假设batch_size = 100, 样本数m = 10000
那么小批量梯度下降形式：
repeat {
         for i = 1, ..., 10000 {
                
        }
}

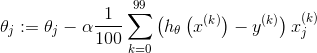
下图显示了三种梯度下降收敛过程：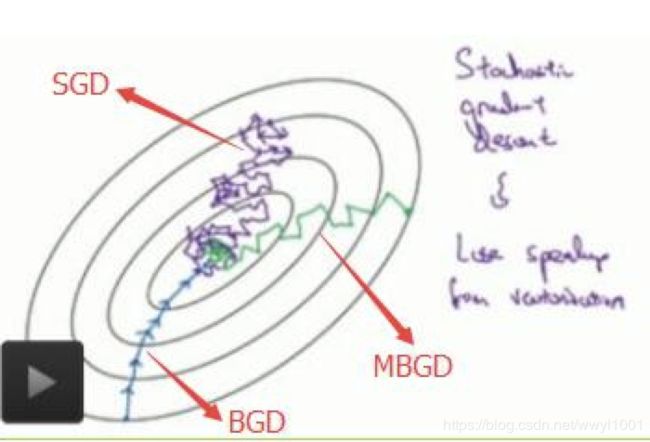

收敛速度：BGD > MBGD > SGD

 

参考：
1. 理解梯度下降
2. 三种形式：https://www.cnblogs.com/lliuye/p/9451903.html
3. 如何直观形象的理解方向导数与梯度以及它们之间的关系？