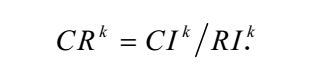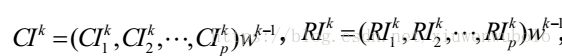数学建模笔记(一)层级分析法(写给自己看的)
层次分析法(多层次权重解析方法)的思路为通过分析复杂系统所包含的因素及相关关系,把一个复杂的问题分解成各个组成因素,并将这些因素按支配关系分组,从而客观上形成多层次的有序的递减层次关系。
这种方法将定性分析和定量分析相结合。实际上这种方法掺杂了很多主观因素,而1——9标度实现了将心理上的定性转化为定量的数值去描述问题。将这种数值构造出判断矩阵,再通过数学手段计算出权重,用权重来对问题进行判断。具体过程归结为:
一般的决策问题可以分为3个层次。最上层为目标层,即你想要决策的问题;中间层为准则层,即影响决策的因素;最下层为方案层,即列举参与决策的方案。将准则层中的各个方案进行两两比较,得到准则对目标的重要性权重。再针对每个准则,对各个可行性方法进行两两比较,得到方案对于准则的重要性权重。
如图为某城市需要改善商场的交通环境而构建的层次结构
1.矩阵构造
构造准则目标的矩阵为:通车能力和方便群众,基建费用,交通安全,市容美观哪个更重要?用1——9标度表示。。接着方便群众的准则再和其他四项比。。。依次来就可以得到一个准则目标的矩阵。随后的方案准则矩阵也这样构造。
2.矩阵的一致性问题
由于决策者构造矩阵存在心理偏差,因此构造的矩阵可能不是完全一致性矩阵,
但是Saaty提出,可对这种不一致性有一定的容忍性。并可以将构造矩阵的最大特征值对应的归一化特征向量作为权向量。MATLAB代码如下:
特征根法求权向量
%% AHP矩阵
a=[1 3 5 3 5
1/3 1 3 1 3
1/5 1/3 1 1/3 3
1/3 1 3 1 3
1/5 1/3 1/3 1/3 1]
[v,d]=eig(a)a =
1.0000 3.0000 5.0000 3.0000 5.0000
0.3333 1.0000 3.0000 1.0000 3.0000
0.2000 0.3333 1.0000 0.3333 3.0000
0.3333 1.0000 3.0000 1.0000 3.0000
0.2000 0.3333 0.3333 0.3333 1.0000
v =
1 至 4 列
-0.8414 + 0.0000i 0.8474 + 0.0000i 0.8474 + 0.0000i -0.9299 + 0.0000i
-0.3532 + 0.0000i 0.0481 + 0.3010i 0.0481 - 0.3010i 0.2398 + 0.0000i
-0.1743 + 0.0000i -0.2680 - 0.0403i -0.2680 + 0.0403i -0.1293 + 0.0000i
-0.3532 + 0.0000i 0.0481 + 0.3010i 0.0481 - 0.3010i 0.2398 + 0.0000i
-0.1098 + 0.0000i 0.0377 - 0.1456i 0.0377 + 0.1456i 0.0591 + 0.0000i
5 列
-0.0000 + 0.0000i
-0.7071 + 0.0000i
-0.0000 + 0.0000i
0.7071 + 0.0000i
0.0000 + 0.0000i
d =
1 至 4 列
5.2067 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i -0.0183 + 1.0343i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i -0.0183 - 1.0343i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.1702 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
5 列
0.0000 + 0.0000i
0.0000 + 0.0000i
0.0000 + 0.0000i
0.0000 + 0.0000i
-0.0000 + 0.0000i
找到d的最大值,再将对应v的某子列归一化,得到权向量。归一化后结果如下:
w=v(:,1)/sum(v(:,1))
w =
0.4593
0.1928
0.0951
0.1928
0.0599
前面有说构造矩阵容忍度的问题,为了衡量,Saaty定义了一致性指标:
CI越小,标明一致性越好,而算出CI以后,将CI与RI相除得到一致性比率CR,当CR<0.1时说明矩阵A在容许范围内,特征向量可以用。(待补充5个方案准则向量,其实求解过程一致的)
下面考虑的是各个准则对目标的权向量和各个方案对每一准则的权向量综合分析,五个矩阵合成一个矩阵再和准则目标矩阵相乘。得到最终的组合权重。定性描述以上过程其实就是,把准则对目标的影响通过权重算出来,再将方案里每个准则的权重算出来,相乘以后得到的是方案对目标的权重(待补充一个抽象一点的思维图)。但是这个组合权重还是不能直接用,还要对其进行一次一致性检验。具体为:
最后如果通过一致性检验则权向量可用。接下来直接看权重哪个大,那么对应方案就是最优方案。实际上当你构造出所有矩阵的那一刻,你心理已经对结果有逼数了。曾经做过一个用层析分析法的电脑选购问题的题目,上网看电脑时候就想买的那个电脑在最后的计算结果上,权重比其他电脑型号大很多:
当时想买四号电脑,结果权重就特别大。
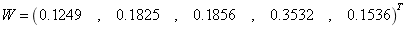
3. 由于构造矩阵比较粗糙,这里有三种近似的求解权向量的方法
%% AHP矩阵
a=[1 3 5 3 5
1/3 1 3 1 3
1/5 1/3 1 1/3 3
1/3 1 3 1 3
1/5 1/3 1/3 1/3 1]
s0=sum(a,1);
[m,n]=size(a);
for j=1:m;
b(:,j)=a(:,j)/s0(j);
end
%和积法
w=sum(b,2);
w1=w/sum(w)
%方根法
w=geomean(b,2);
w2=w/sum(w)
%对数最小偏差法
w=geomean(a,2);
w3=w/sum(w)
结果
w1 =
0.4563
0.1915
0.0991
0.1915
0.0616
w2 =
0.4614
0.1946
0.0909
0.1946
0.0586
w3 =
0.4614
0.1946
0.0909
0.1946
0.0586