Tensorflow 入门学习14.TensorFlow实现LeNet5实例

本文学习内容来自《TensorFlow深度学习应用实践》

LeNet5网络结构

在计算机视觉中卷积神经网络取得了巨大的成功，它在工业上以及商业上的应用很多，一个商业上最典型的应用就是识别支票上的手写数字的LeNet5神经网络。从20世纪90年代开始美国大多数银行都用这种技术识别支票上的手写数字。
实际应用中的LeNet5卷积神经网络共有8层，其中每层都包含可训练的神经元，而连接神经元的是每层的权重。

8层LeNet5神经网络。

INPUT

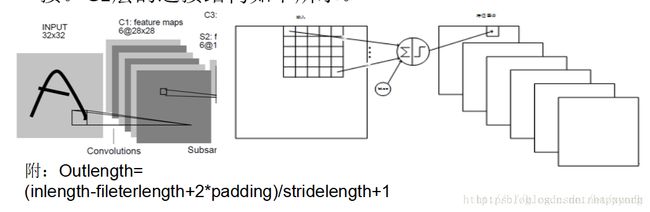
首先对于INPUT层来说，这是数据的输入层，在原始模型框架中，输入图像大小为[32,32]，这样能够将所有的手写信息被神经网络感受到。

C1

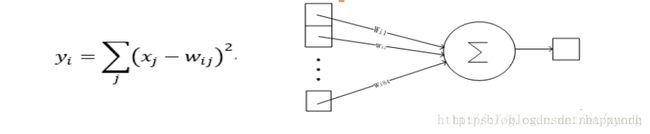
第一个卷积层C1是最初开始进行卷积计算的层，形成6个特征图谱。卷积层特征的计算公式：
$$x^i=f((\sum x_i^{i-1}\ast K_{ij}^l)+b_j^i)$$
其中$x_i^{i-1}\ast K_{ij}^l$表示从第1层到l+1层要产生的feature数量，即5*5=25个；
b代表 bias的数量，这里的bias是1。

卷积的输入区域大小是5x5，每个特征图谱内参数共享，即每个特征图谱内只使用一个共同卷积核，卷积核有5x5个连接参数加上1个偏置共26个参数。卷积区域每次滑动一个像素，这样卷积层形成的每个特征图谱大小是(32-5)/1+1=28x28。C1层共有6*(55+1)=156个训练参数，对于C1层来说，每个像素都与前一个输入层的像素相连接，因此对于C1层，总共有15628*28=122304个连接。C1层的连接结构如下所示。

C1层连接结构：

LeNet5 C1到S2层的连接如下图所示：

S2

S2是一个下采样层。这里是C1中的[2,2]区域内的像素求和再加上一个偏置，然后将这个结果再做一次映射（sigmoid等函数），所以相当于对S1做了降维，此处共有62=12个参数。S2中的每个像素都与C1中的22个像素和1个集团相连接，所以有6514*14=5880个连接。

S2到C3

LeNet5最复杂的就是S2到C3层，其连接如图所示：

前6个feature map与S2层相连的3个feature map相连接，后面6个feature map与S2层相连的4个feature map相连接，后面3个feature map与S2层部分不相连的4个feature map相连接，最后一个与S2层的所有feature map相连。卷积核大小依然是55，所以总共有6(355+1)+6*(455+1)+3*(455+1)+1*(655+1)=1516个参数。而图像大小为10*10，所以共有151600个连接。

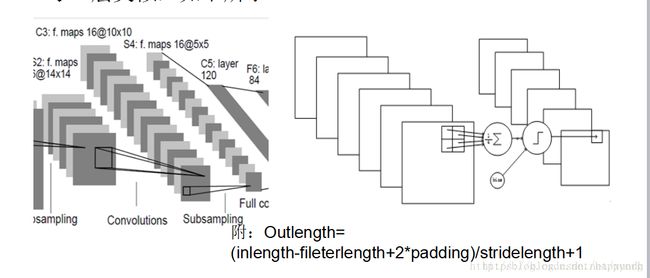
C3

C3层也是一个卷积层

S4

S4是一个下采样Pooling层，窗口大小仍然是22，共计16个feaure map，所以32个参数。16（25*4+25）=2000个连接。

C5

C5是卷积层，共120个feature map，每个feature map 与S4层所有的feature map相连接，卷积核大小是55，而S4层feature map大小也是55，所以C5的feature map就变成了1个点，共计有128*(25*16+1)=48120个参数。

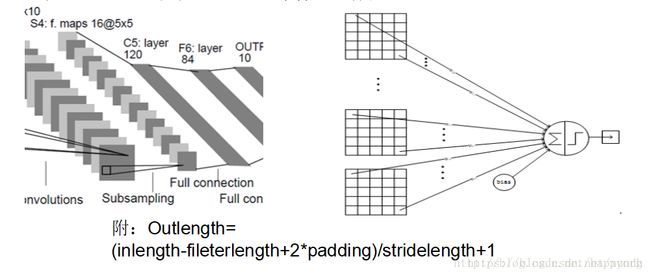
F6

最后一个F6层也是全连接层，有84个节点，所以有84*(120+1)=10164个参数。F6层采用了正切函数，计算公式为：
$$x^i=f(a_i)=tanh(a_i)$$

输出层

最后是输出层，以上这8层合在一起构成了LeNet5神经网络的全部结构。

TensorFlow实现LeNet实例

本节逐步对LeNet5中的每一层进行分解，会对神经元的个数、隐藏层的层数以及学习率等神经网络关键参数做出调整，观察模型训练的时间。

代码：

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time

x = tf.placeholder('float', [None, 784])
y_ = tf.placeholder('float', [None, 10])

x_image = tf.reshape(x, [-1, 28, 28, 1])

# 第一个卷积层
# 初始化卷积核和偏置值
filter1 = tf.Variable(tf.truncated_normal([5, 5, 1, 6]))  # 卷积核是由5*5大小的卷积，输入为1个通道而输出为6个通道
bias1 = tf.Variable(tf.truncated_normal([6]))  # 生成的偏置值与卷积结果进行求和的计算
conv1 = tf.nn.conv2d(x_image, filter1, strides=[1, 1, 1, 1], padding='SAME')
h_conv1 = tf.nn.sigmoid(conv1 + bias1)  # 求得第一个卷积层输出结果

# maxPooling池化层，对于2*2大小的框进行最大特征取值
maxPool2 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

filter2 = tf.Variable(tf.truncated_normal([5, 5, 6, 16]))
bias2 = tf.Variable(tf.truncated_normal([16]))
conv2 = tf.nn.conv2d(maxPool2, filter2, strides=[1, 1, 1, 1], padding='SAME')
h_conv2 = tf.nn.sigmoid(conv2 + bias2)

maxPool3 = tf.nn.max_pool(h_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

# 第三层 卷积层，这里需要进行卷积计算后的大小为[10,10,16]，其后的池化层将特征进行再一次压缩
filter3 = tf.Variable(tf.truncated_normal([5, 5, 16, 120]))
bias3 = tf.Variable(tf.truncated_normal([120]))
conv3 = tf.nn.conv2d(maxPool3, filter3, strides=[1, 1, 1, 1], padding='SAME')
h_conv3 = tf.nn.sigmoid(conv3 + bias3)

# 后面2个全连接层，全连接层的作用在整个卷积神经网络中起到“分类器”的作用
# 即将学到的“分布式特征表示”映射 到样本标记空间的作用

# 权值参数
W_fc1 = tf.Variable(tf.truncated_normal([7 * 7 * 120, 80]))
# 偏置值
b_fc1 = tf.Variable(tf.truncated_normal([80]))
# 将卷积的输出展开
h_pool2_flat = tf.reshape(h_conv3, [-1, 7 * 7 * 120])
# 神经网络计算，并添加sigmoid激活函数
h_fc1 = tf.nn.sigmoid(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# 输出层，使用softmax进行多分类
# 这里对池化后的数据进行重新展开，将二维数据重新展开成一维数组之后计算每一行的元素个数。最后一个输出层在使用了softmax进行概率的计算
W_fc2 = tf.Variable(tf.truncated_normal([80, 10]))
b_fc2 = tf.Variable(tf.truncated_normal([10]))
y_conv = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)

# 最后是交叉熵作为损失函数，使用梯度下降来对模型进行训练
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(cross_entropy)

sess = tf.InteractiveSession()

# 测试正确率
corrent_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(corrent_prediction, "float"))

# 所有变量进行初始化
sess.run(tf.initialize_all_variables())

# 获取mnist数据
mnist_data_set = input_data.read_data_sets('MNIST_data', one_hot=True)
# 进行训练
start_time = time.time()
for i in range(20000):
    # 取训练数据
    batch_xs, batch_ys = mnist_data_set.train.next_batch(200)

    # 每迭代100 个batch,对当前训练数据进行测试，输出当前预测准确率
    if i % 2 == 0:
        train_accuracy = accuracy.eval(feed_dict={x: batch_xs, y_: batch_ys})
        print("step %d, training accuracy %g" % (i, train_accuracy))
        # 计算间隔时间
        end_time = time.time()
        print('time:', (end_time - start_time))
        start_time = end_time

        # 训练数据
        train_step.run(feed_dict={x: batch_xs, y_: batch_ys})

# 关闭会话
sess.close()

运行结果：

使用ReLU激活函数代替sigmoid

对于神经网络模型来说，首先重要的一个目标就是能够达到最好的准确率，这需要通过设计不同的模型和算法完成。其次在模型的训练过程中一般要求能够在最短的时间内达到收敛。

相较于sigmoid和tanh 函数，ReLU主要有以下优点：

• 收敛快：对于SGD的收敛有巨大的加速作用，可以看到对于达到阈值的数据其激活力度是随数值的加大而增大，且呈现一个线性关系。
• 计算简单：ReLU的算法较为简单，单纯一个值的输入输出不需要进行一系列的复杂计算，从而获得激活值。
• 不易过拟合：使用ReLU进行模型计算时，一部分神经元在计算时如果有一个过大的梯度经过，则次神经元的梯度会强行设置为0，而在整个其后的训练过程中这个神经元都不会被激活，这会导致数据多样化的丢失，但是也能防止过拟合，这个现象一般不被注意到。

把上面程序里的sigmoid换为Relu，可以看到训练准确度并没有提高，反而是在比较低的水平。不同的学习率对ReLU模型的训练会有很大影响，准确率设置不当会造成大量的神经元被锁死。这里需要减少模型的学习率。

函数重构——模块化设计

上面的程序里为了模型的正常使用，在图计算过程中需要使用大量的权重值和偏置量。这些都是由TensorFlow变量所设置。而变量带来的问题就是每次图对话计算过程中都要被反复初始化和赋予新值。

#!/usr/bin/python
# -*- coding: UTF-8 -*-

from PIL import Image, ImageFilter
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time
import matplotlib.pyplot as plt
import numpy as np


def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


# 初始化单个卷积核上的偏置值
def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


# 输入特征 x，用卷积核W进行卷积运算，strides 为卷积核移动步长，
# padding 表示是否需要补齐边缘像素使输出图像大小不变
def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')


# 对 x 进行最大池化操作，ksize进行池化的范围
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')


# 自己输入的图片进行预测
def imageprepare(path):
    im = Image.open(path)    #读取的图片所在路径，注意是28*28像素
    im.show()
    im = im.convert('L')
    tv = list(im.getdata())
    tva = np.array([x*1.0/255.0 for x in tv])
    return tva


sess = tf.InteractiveSession()

# 声明输入图片数据、类别
x = tf.placeholder('float', [None, 784])
y_ = tf.placeholder('float', [None, 10])
# 输入图片数据化
x_image = tf.reshape(x, [-1, 28, 28, 1])

W_conv1 = weight_variable([5, 5, 1, 6])
b_conv1 = bias_variable([6])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

W_conv2 = weight_variable([5, 5, 6, 16])
b_conv2 = bias_variable([16])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

W_fc1 = weight_variable([7 * 7 * 16, 120])
# 偏置值
b_fc1 = bias_variable([120])
# 将卷积的输出展开
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 16])
# 神经网络计算，并添加relu激活函数
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

W_fc2 = weight_variable([120, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)

# 代价函数
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
# 使用Adam优化算法来调整参数
train_step = tf.train.GradientDescentOptimizer(1e-4).minimize(cross_entropy)

# 测试正确率
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float32"))

# 变量初始化
sess.run(tf.initialize_all_variables())

# 获取mnist数据
mnist_data_set = input_data.read_data_sets('MNIST_data', one_hot=True)
c = []

# 进行训练
start_time = time.time()
for i in range(300):
    # 获取训练数据
    batch_xs, batch_ys = mnist_data_set.train.next_batch(200)
    # 每迭代10个batch，对当前训练数据进行测试，输出当前预测准确率
    if i % 10 == 0:
        train_accuracy = accuracy.eval(feed_dict={x: batch_xs, y_: batch_ys})
        c.append(train_accuracy)
        print("step %d , training accuracy %g" % (i, train_accuracy))
        # 计算间隔时间
        end_time = time.time()
        print('time:', (end_time - start_time))
        start_time = end_time
    # 训练数据
    train_step.run(feed_dict={x: batch_xs, y_: batch_ys})

plt.plot(c)
plt.tight_layout()
plt.savefig('cnn-tf-cifar10-2.png', dpi=200)

path = './mnist_train/train_6.bmp'
test_image = imageprepare(path)
prediction = tf.argmax(y_conv, 1)
result = prediction.eval(feed_dict={x: [test_image]}, session=sess)
print('输入的图片:' + path + ' 识别结果=' + str(result[0]))

sess.close()

输出准确率：

卷积核和隐藏层参数的修改

通过调整激活函数和学习率程序学习效率会有非常大的提高。除此之外深度学习中有不同的隐藏层和每层包含的神经元，而通过调节这些神经元和隐藏层的数目，也可以改善神经网络模型的设计。
下面修改每个隐藏层中神经元的数目，即第一次生成了32个通道的卷积层，第二层为64，而在全连接阶段使用了1024个神经元作为学习参数。

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time
import matplotlib.pyplot as plt


def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


# 初始化单个卷积核上的偏置值
def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


# 输入特征 x，用卷积核W进行卷积运算，strides 为卷积核移动步长，
# padding 表示是否需要补齐边缘像素使输出图像大小不变
def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')


# 对 x 进行最大池化操作，ksize进行池化的范围
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')


sess = tf.InteractiveSession()

# 声明输入图片数据、类别
x = tf.placeholder('float', [None, 784])
y_ = tf.placeholder('float', [None, 10])
# 输入图片数据化
x_image = tf.reshape(x, [-1, 28, 28, 1])

W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

W_fc1 = weight_variable([7 * 7 * 64, 1024])
# 偏置值
b_fc1 = bias_variable([1024])
# 将卷积的输出展开
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
# 神经网络计算，并添加relu激活函数
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)

# 代价函数
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
# 使用Adam优化算法来调整参数
train_step = tf.train.GradientDescentOptimizer(1e-4).minimize(cross_entropy)

# 测试正确率
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float32"))

# 变量初始化
sess.run(tf.initialize_all_variables())

# 获取mnist数据
mnist_data_set = input_data.read_data_sets('MNIST_data', one_hot=True)
c = []

# 进行训练
start_time = time.time()
for i in range(1000):
    # 获取训练数据
    batch_xs, batch_ys = mnist_data_set.train.next_batch(200)
    # 每迭代10个batch，对当前训练数据进行测试，输出当前预测准确率
    if i % 2 == 0:
        train_accuracy = accuracy.eval(feed_dict={x: batch_xs, y_: batch_ys})
        c.append(train_accuracy)
        print("step %d , training accuracy %g" % (i, train_accuracy))
        # 计算间隔时间
        end_time = time.time()
        print('time:', (end_time - start_time))
        start_time = end_time
    # 训练数据
    train_step.run(feed_dict={x: batch_xs, y_: batch_ys})

sess.close()
plt.plot(c)
plt.tight_layout()
plt.savefig('cnn-tf-cifar10-1.png', dpi=200)

（此代码未调试成功，实际运行时准确率相当低）
随着卷积核数目的增加，准确率上升的速度也非常快，但训练的速度明确变慢了。