基于深度学习的推荐(五)：CTR预测经典模型PNN

公众号

关注公众号:推荐算法工程师,输入"进群",加入交流群,和小伙伴们一起讨论机器学习,深度学习,推荐算法.

前言

PNN模型是上交大和UCL（University College London）在ICDM 2016上提出的。product思想来源于，在ctr预估中，认为特征之间的关系更多是一种and“且”的关系，而非add"加”的关系。例如，性别为男且喜欢游戏的人群，比起性别男和喜欢游戏的人群，前者的组合比后者更能体现特征交叉的意义[1]。这和FM的特征交叉思想类似。FM是进行one-hot编码特征的交叉，而PNN则是将特征embedding后，加入向量积product层，从而进行特征间的交叉。那么这个Product到底是如何实现的呢？论文的公式写得有点复杂，本文从简介绍，阅读大概需要三分钟。

论文链接：https://arxiv.org/abs/1807.00311 或 https://arxiv.org/pdf/1611.00144.pdf

1.向量内积与向量外积

1.1 向量内积Inner Product

Inner Product就是a,b两个向量对应元素相乘的和[3]，或者对a的转置与b使用矩阵乘法：

1.2 向量外积Outer Product

Outer Product就是列向量与行向量相乘，结果是一个矩阵[3]：

1.3 向量点积Dot Product

点积有个别名，叫内积，又叫标量积，向量的积。只不过，提起内积我们常想到的是1.1中的代数定义，而提起点击，常想到的是如下的几何定义[3]：

1.4 向量叉积Cross Product

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算[2]，外积的方向根据右手法则确定[3]：

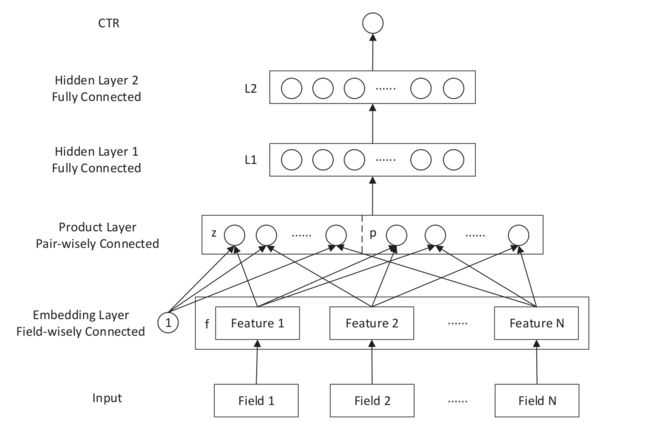
2. 模型结构

首先是Input层，比如一个样本有三个field，男/女，胖/瘦，高/矮，每个field的取值数分别有2,2,2个，那么形如(0,1,0,1,0,1)的样本就是一条输入x。

Embedding layer就是将x进行映射，比如映射后的维度embed_size为k，假设每个field只有一个非零值，那么embed_x的维度就是field_size*k=3k维。

前两层大家都很熟悉，重点看下product层。product层的左侧z是线性部分，将embedding layer层获得的特征串联起来就是z。右边p是特征交叉部分，根据交叉方式不同，product层分为两种，第一种是采取向量内积的IPNN，第二种是采取向量外积的OPNN。

2.1 IPNN

回顾一下，向量内积，简单说就是两个向量相乘，返回一个实数值的运算。假设field_size为n，那么通过内积获得的特征维度node_size=n(n-1)/2。因此，当使用Inner Product内积时，Product Layer的特征维度就是：field_sizeembed_size+field_size(field_size-1)/2*。

2.2 OPNN

回顾一下，向量外积Outer product，两个向量相乘返回一个矩阵。通过外积可以在Product Layer获得的矩阵个数为：field_size*(field_size-1)/2。内积的结果可以直接串联，拼接到特征上，矩阵该如何拼接呢？论文中使用了sum pooling的方法，对每个矩阵进行sum求和，得到实数值，然后拼接到z上:

因此，使用Outer Product外积时，Product Layer的特征维度仍然为：field_sizeembed_size+field_size(field_size-1)/2。

3. 代码实战

3.1 数据

论文中使用的是Criteo和iPinyou数据，太大了。本文使用一个小数据来测试，数据和之前fnn博客中的相同。共有22个field,各field中属性取值的可枚举个数为:

FIELD_SIZES = [1037, 151, 59, 1603, 4, 333, 77890, 1857, 9, 8, 4, 7, 22, 3, 92, 56, 4, 920, 38176, 240, 2697, 4]

样本x则被划分为:

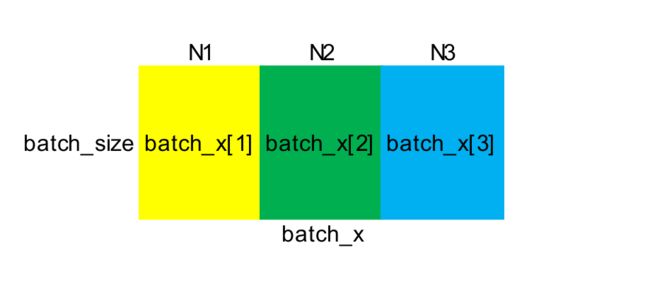
由于是模拟CTR预估,所以标签y是二分类的,实验中y∈{0,1}.

3.3 内积和外积的实现

设embedding的向量维度为k，num_inputs为n，num_pairs为p。内积的实现如下：

    row = [] # num_pairs
    col = [] # num_pairs
    for i in range(num_inputs-1):
        for j in range(i+1, num_inputs):
            row.append(i)
            col.append(j)
    
    p = tf.transpose(
            tf.gather(
            tf.transpose(xw3d, [1,0,2]), # [num_inputs, batch, k]
            row), # [num_pairs, batch, k]
            [1,0,2]) # [batch, num_pairs, k]
    
    q = tf.transpose(
            tf.gather(
            tf.transpose(xw3d, [1,0,2]), # [num_inputs, batch, k]
            col), # [num_pairs, batch, k]
            [1,0,2]) # [batch, num_pairs, k]
    
    p = tf.reshape(p, [-1, num_pairs, embed_size]) # [batch, num_pairs, k]
    q = tf.reshape(q, [-1, num_pairs, embed_size]) # [batch, num_pairs, k]
    
    ip = tf.reshape(tf.reduce_sum(p*q, [-1]), [-1, num_pairs])
    l = tf.concat([xw, ip], 1) # [num_inputs*k + num_pairs]
    
    for i in range(len(layer_sizes)):
        w = self.vars['w%d'%i]
        b = self.vars['b%d'%i]
        l = utils.activate(tf.matmul(l, w)+b, layer_acts[i])
        l = tf.nn.dropout(l, self.layer_keeps[i])

外积部分并没有直接求field_size*(field_size-1)/2个矩阵，而是借助了一个中间矩阵W（shape为(k,p,k)）来实现，这样求得的sum pooling是带有权重的，当w全为1时，才是公式中直接的sum pooling。

    row = [] # num_pairs
    col = [] # num_pairs
    for i in range(num_inputs-1):
        for j in range(i+1, num_inputs):
            row.append(i)
            col.append(j)
    
    p = tf.transpose(
            tf.gather(
            tf.transpose(xw3d, [1,0,2]), # [num_inputs, batch, k]
            row), # [num_pairs, batch, k]
            [1,0,2]) # [batch, num_pairs, k]
    
    q = tf.transpose(
            tf.gather(
            tf.transpose(xw3d, [1,0,2]), # [num_inputs, batch, k]
            col), # [num_pairs, batch, k]
            [1,0,2]) # [batch, num_pairs, k]
    
    p = tf.reshape(p, [-1, num_pairs, embed_size]) # [b, p, k]
    q = tf.reshape(q, [-1, num_pairs, embed_size]) # [b, p, k]
    
    # k全为1时，就是严格按照公式
    p = tf.expand_dims(p, 1) # [batch, 1, p, k]
    k = self.vars['kernel'] # [k, p, k]
    ip = tf.multiply(k, p) # [batch, k, p, k]
    ip = tf.reduce_sum(ip, axis=-1) # [batch, k, p]
    ip = tf.transpose(ip, [0, 2, 1]) # [batch, p, k]
    ip = tf.multiply(ip, q) # [batch, p, k]
    ip = tf.reduce_sum(ip, axis=-1) # [batch, p]
    
    l = tf.concat([xw, ip], 1) # [num_inputs*k + num_pairs]
    
    for i in range(len(layer_sizes)):
        w = self.vars['w%d'%i]
        b = self.vars['b%d'%i]
        l = utils.activate(tf.matmul(l, w)+b, layer_acts[i])
        l = tf.nn.dropout(l, self.layer_keeps[i])

论文开源代码：https://github.com/Atomu2014/product-nets
本文完整数据和代码：https://github.com/wyl6/Recommender-Systems-Samples/tree/master/RecSys%20And%20Deep%20Learning/DNN/pnn

参考

[1] https://zhuanlan.zhihu.com/p/43693276

[2] https://baike.baidu.com/item/%E5%90%91%E9%87%8F%E5%A4%96%E7%A7%AF/11031485?fr=aladdin

[3] https://blog.csdn.net/minmindianzi/article/details/84820362